ترجمههای کامران بزرگزاد

روشهای استاندارد برای نوشتن اعداد بزرگ
چند نمونه از اعداد بزرگ در ریاضیات
اعداد بزرگ جدید جواب چه مسائلی هستند؟
این مقاله
ادامه مقاله قبل درباره
اعداد بزرگ است. در این بخش بیشتر به چگونگی نوشتن اعداد بزرگ میپردازیم.
همانطور
که در بخش
قبل توضیح داده شد، یکی از روشها برای نمایش اعداد استفاده از نمادگذاری
علمی است. ولی این روش بیشتر برای نمایش اعداد در علومی مثل فیزیک و شیمی
کاربرد دارد. نمایش اعداد بزرگی که در ریاضیات (مُدرن) با آنها مواجه میشویم به
این روش غیر ممکن است. ضمناً نمایش آنها باید طوری باشد که بتوانیم آنها را به
آسانی از نظر کوچکی و بزرگی مرتب کنیم، و بگوییم کدام یک از دیگری بزرگتر یا
کوچکتر است.
مثلاً در
نمادگذاری علمی اگر ما بخواهیم دو عدد 5×104 و 2×105 را با هم
مقایسه کنیم، ابتدا توانها را با هم مقایسه میکنیم، که دراینصورت، بدلیل اینکه 5>4،
پس 2×105 از 5×104 بزرگتر است. اگر توانها با هم مساوی بودند، ما ضرایب را با هم مقایسه میکنیم،
پس چون 5>2، بنابراین 5×104 > 2×104.
همانطور که در بخش اول مقاله ذکر شد،
نمایش اعداد بزرگ مستلزم استفاده از عملیاتی بالاتر از به توان رساندن است که ما
از کلاس پنجم/ششم با آن آشنایی داریم. به منظور درک بهتر عمل بعد از توان، که به
آن عمل رده-4 (tetration)، یا اَبَرعمل-4 (hyper-4) گفته میشود، لازم است مروری داشته باشیم بر
روی 3 عمل ابتدایی (ما در اینجا از عملهای تفریق و تقسیم و ریشه گرفتن صرفه نظر
میکنیم، چون در حقیقت آنها جزء عملهای افزایش دهنده نیستند):
* عمل
جمع:
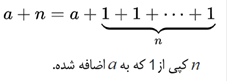
* عمل
ضرب:

* عمل توان:
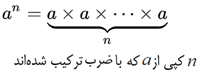
* عمل رده چهارم (اَبَر-4):
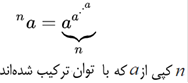
ولی
برخلاف سه عمل اول، عمل رده-چهارم (اَبَر-4) جزء توابع مقدماتی (elementary
function) محسوب نمیشود. به طریقه نوشتن
عمل ابر-4 دقت کنید؛ برخلاف توان معمولی که توان در سمت راست پایه قرار میگیرد،
ابر-4 بصورت
na
نوشته میشود
. در اینجا a پایه (base)، و n ارتفاع (height) نامیده میشود. برای کلیه nها، رابطه زیر برقرار است:

برخی
اوقات عملِ ابر-4 برج توان (power
tower) نیز نامیده میشود، ولی این میتواند گمراه کننده
باشد، زیرا ما در توان معمولی هم میتوانیم برج توانی داشته باشیم، برای روشن شدن
این مورد به مثالهای زیر توجه کنید:
مثلاً یک
برج توان ابر-4 از مرتبه n بصورت زیر نمایش داده میشود:
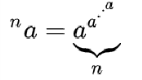
ولی همین
برج را میتوان برای توان معمولی نیز در نظر گرفت:
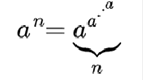
پس تفاوت
این دو در چیست و چگونه محاسبه میشوند؟ توان معمولی از پایین به بالا محاسبه میشود،
ولی ابر-4 از بالا به پایین. مثلاً
42
از بالا
به پایین بصورت زیر محاسبه میشود:
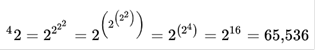
ولی برج
توانِ معمولی ![]() از پایین به بالا بصورت زیر
محاسبه میشود:
از پایین به بالا بصورت زیر
محاسبه میشود:
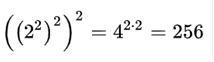
بنابراین ![]() .
.
همانطور که ذکر شد رشد ابر-4 نسبت به توان معمولی،
یا حتی فاکتوریل، بسیار بیشتر است. برای اینکه ایدهای از بزرگی رشد ابر-4 داشته
باشد، ابر-4 را روی اعداد 1 الی 10 بعنوان پایه اعمال کردهایم، و ارتفاع آن را هم
از 3 بالاتر نبردهایم:
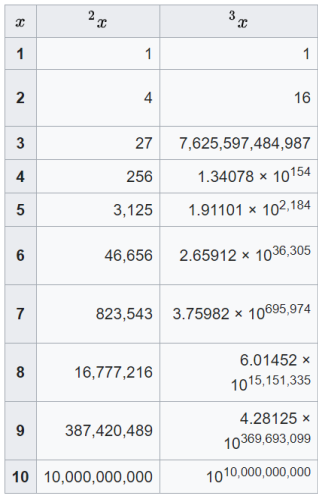
برای مقایسه، 102=100، و 103=1000 است. ولی همانطور که مشاهده میکنید 10 3 مساوی 1010,000,000,000 است، یعنی یک عدد دهمیلیارد رقمی!
اگر ارتفاع را زیاد کنیم، و حتی پایه
کوچکی مثل 2 را نیز انتخاب کنیم، 2 6 بقدری بزرگ است که
نمیتوان آن را بصورت نمادگذاری علمی بیان کرد. اصولاً در نمادگذاری علمی توان نشاندهنده طول عدد
است (مانند مثال بالا که در آن 1010,000,000,000 یک عدد دهمیلیارد رقمی است). ولی اگر توان آنقدر بزرگ باشد که نامی برای آن نباشد، یا حتی نتوانیم
طولی را برای آن تصور کنیم، آنوقت تکلیف چیست؟ مثلاً عدد معروف گوگُل (googol) یک عدد صد رقمی است
(10100)، ولی طول عدد گوگلپلکس
(googolplex)،
که یعنی ده به توان گوگُول:
googolplex = 10googol
بقدری بزرگ
است که جا برای نوشتن آن روی کل ذرات عالم نیست. بااینحال، همانطور که در بخش نخست
مقاله ذکر شد، عدد گوگلپلکس در مقابل اعدادی که امروزه بزرگ محسوب میشوند بسیار
کوچک است. همینجاست که عملیات رده بالا مطرح میشوند و از آنها بجای توان استفاده
میشود. ولی ما فقط از ابر-4 بعنوان عمل بعدی سخن گفتیم. آیا عملیاتی بالاتر از
ابر-4 نیز امکانپذیر است؟ البته که امکانپذیر است، در ریاضیات هیچ چیز نمیتواند
جلوی تعمیم موضوعات و گسترش آنها را بگیرد. عمل بعد از ابر-4، ابر-5 یا (pentation) نامیده میشود، و
سرعت رشد آن نسبت به عملیات قبلی بسیار بیشتر است. ولی چگونه میتوان این عمل را
نمایش داد؟ نمایش ابر عملهای رده بالا به نمادگذاریهای خاصی نیاز دارد تا بتوان
آنها را تعمیم داد. زیرا دیگر جایی برای جابجایی پایه و توان وجود ندارد تا بتوان
آن را نسبت به توان معمولی یا ابر-4 متمایز کرد. به این منظور نمادگذاریهای
مختلفی ابداع شده، که دو تا از معروفترین آنها یکی نمادگذاری پیکان-سربالای
کنوث (Knuth's up-arrow
notation) است، و دیگری نمادگذاری پیکان زنجیرهای کانوی
(Conway chained arrow notation).
نمادگذاری اول توسط ریاضیدان و استاد علوم رایانهای دونالد کنوث، و دومی
توسط ریاضیدان فقید جان هورتون کانوی ابداع شد. کنوث ریاضیدانی است که در
حوزه علوم رایانهای بسیار مشهور است و از استادان بازنشسته و بنام این رشته بحساب
میآید. کانوی هم ریاضیدان مشهوری بود که متاسفانه در سال 2020 به علت ابتلاء به
کرونا درگذشت.
همانطور
که از نام آن پیداست، نمادگذاری پیکانسربالای کنوث برای نمایش عملیات رده
بالا از پیکانهای سربالا استفاده میکند. مثلاً برای نمایش توان معمولی از یک
پیکان (↑)،
برای ابر-4 از دو پیکان (↑↑)، برای ابر-5 از سه
پیکان (↑↑↑)، و ... استفاده میکند.
بنابراین
در این نمادگذاری، برای توان معمولی داریم:
![]()
برای
ابر-4:
![]()
و برای
ابر-5:

به این
ترتیب، تعریف کلی عملِ ابر-n
بصورت ![]() خواهد بود، که n
نشاندهنده n
پیکانسربالا است. پس در عبارت
زیر که یک ابر-6 را نمایش میدهد،
خواهد بود، که n
نشاندهنده n
پیکانسربالا است. پس در عبارت
زیر که یک ابر-6 را نمایش میدهد،
![]()
n برابر 4، و a و b هم 2 و 3 هستند.
نمادگذاری
دیگری که برای نمایش اعداد بزرگ بکار میرود پیکان زنجیرهای کانوی است که
نمونهای از آن شبیه زیر میباشد:
![]()
نمادگذاری
زنجیرهای نسبت به پیکان سربالا قویتر است و میتواند اعداد بزرگتری را نمایش
دهد. تعریف آن بر اساس یک سری قواعد ترکیبی و بازگشتی (recursive) میباشد، که بطور اجمالی
آنها را بیان میکنم:
قاعده 1:
یک زنجیره خالی (یا زنجیرهای با طول 0)
با 1 مساوی است، و زنجیره p نشاندهنده عدد p است.
قاعده 2: ![]() با X مساوی است.
با X مساوی است.
قاعده 3: ![]() با
با ![]() در نمادگذاری کنوث مساوی است.
در نمادگذاری کنوث مساوی است.
قاعده 4: ![]() با
با ![]() مساوی است.
مساوی است.
(با p کپی از X، p-1 کپی از q، و p-1
کپی از پرانتزها، که برای q>0 اعمال میشوند).
قاعده 5:
بدلیل اینکه طبق قاعده 2، ![]() مساوی
مساوی ![]() است، و همچنین طبق قاعده 3
است، و همچنین طبق قاعده 3 ![]() ،
ما میتوانیم
،
ما میتوانیم ![]() را مساوی
را مساوی ![]() تعریف کنیم.
تعریف کنیم.



همانطور
که میبینید با اعدادی کوچکی در حد 2 و 3، و ترکیب آنها در یک زنجیره بطول 4، میتوان
اعداد بسیار بزرگی تولید کرد.
ولی این
پایان راه نیست! ریاضیات مملو از تعمیم است و هر مفهومی را میتوان به مراتب
بالاتر تعمیم داد. من در ادامه همین بخش به اعدادی اشاره میکنم که حتی با
نمادگذاری زنجیرهای نیز نمیتوان آنها را بیان کرد، و نیاز به نمادگذاریهای خاص
خودشان را دارند.
اعداد
بزرگی که در ریاضیات مطرح شدهاند زیاد هستند و من فقط به چندتا از معروفترین
آنها اشاره میکنم.
* اعداد اسکیوز (Skewes's number) که تقریباً از دهه 1930 در نظریه اعداد مطرح
بودهاند. اولین عدد اسکیوز ![]() و دومی
و دومی ![]() است. این دو عدد را براحتی میتوان توسط عمل ابر-4 یا نمادگذاری پیکانسربالای
کنوث نمایش داد.
است. این دو عدد را براحتی میتوان توسط عمل ابر-4 یا نمادگذاری پیکانسربالای
کنوث نمایش داد.
* عدد موزر (Moser's number) 10↑↑↑...↑↑↑10 است، که در
اینجا تعداد پیکانهای سربالا 10↑↑257 عدد است.
* عدد
گراهام (Graham's number)
توسط ریاضیدانان آمریکایی رونالد گراهام مطرح شد و از اوایل دهه 1980 تا
چندین سال بعنوان بزرگترین عدد مطرح در ریاضیات شناخته میشد و در کتاب رکوردهای
گینس نیز نام آن بعنوان بزرگترین عدد آمده بود. مسئلهای که جواب آن عددِ گراهام
است به نوبه خودش جالب است، ولی من برای طولانیتر نشدن این مقاله فقط سعی میکنم
بزرگی آن را در زیر توضیح دهم. برای توضیح این عدد میتوانید به مقاله فارسی
یا انگلیسی
که در ویکیپدیا آمده رجوع کنید. عدد گراهام بعنوان عددی تعریف میشود که ساختن آن
64 مرحله دارد و ساختن هر مرحله از آن بصورت
زیر تعریف میشود:

برای
ساختن عدد گراهام باید 64 مرحله جلو برویم تا g64 ساخته شود. به همان مرحله نخست، یعنی g1، توجه کنید که چقدر بزرگ
است (یک عمل ابر-6 که نمیتوان آن را بصورت توان معمولی نشان داد). و تعداد پیکانهایسربالا در مرحله دوم به
تعداد g1 است، و در
مرحله سوم به تعداد g2، و ... به همین ترتیب تا g64. این عدد در مقایسه با اعداد معروف قبل از خودش بسیار بزرگتر است.
این عدد را بصورت دقیق نمیتوان توسط نمادگذاری زنجیرهای نمایش داد، ولی جالب است
بدانید عدد گراهام (G) مابین دو زنجیره زیر خواهد بود:
![]()
از همینجا قدرت نمادگذاری زنجیرهای معلوم میشود. همانطور
که ذکر شد، عدد گراهام حدود 15 سال رکورد بزرگترین عدد را داشت.
حدود 20 سال است که هر از چندگاهی رکورد اعداد بزرگ را پیگیری میکنم، و باید اشاره کنم که ماهیت اعداد جدیدی که از اواخر دهه 1990 بعنوان رکورددار ”بزرگترین عدد“ مطرح بودهاند
بکلی با اعداد قبلی فرق دارند، طوری که نمیتوان آنها را حتی با نمادگذاری زنجیرهای
کانوی نشان داد.
این اعداد
بیشتر بصورت کرانههای بالایی یا پایینی یک مسئله مطرح میشوند. مثالهایی از این
اعداد اینها هستند:
* TREE(3). عددی است که در
زمینه نظریه درخت کروسکال (Kruskal's
tree theorem) مطرح میشود.
* عدد رآیو (Rayo's number). عددی است که در سال 2007 توسط ریاضیدان مکزیکی
آگوستین رآیو در زمینه نظریه مجموعهها و منطق مطرح شده و از عدد گراهام بزرگتر است.
* عدد گاردن (Garden number). عددی است که باز هم در زمینه نظریه مجموعهها و منطق مطرح شده و گفته میشود از عدد رآیو هم بزرگتر است.
* عدد هولوم (hollom)
که یک عدد بزرگ و جدید در زمینه نظریه مجموعهها و
منطق است.
در طول سالهای گذشته، بین اعداد فوق
نیز، اعداد دیگری مطرح شدهاند که معروفیت کمتری دارند. توضیح این اعداد به زبان
غیر فنی تقریباً غیر-ممکن است، و شرح فنی آنها نیز خارج از حوصله این مقاله است.
حالا اگر کسی بپرسد ”خوب! بزرگی
اعداد فوق در چه حد است؟“، پاسخ این است که بسیار، بسیار، بسیار، ... ، بسیار
بزرگتر از اعداد قبلی. ولی توصیف آنها به نمادگذاریهای خاصی نیاز دارد که عمدتاً
به حوزههایی از نظریه مجموعهها، و منطق ریاضی باز میگردد. ولی لازم میدانم چند
نکته را در رابطه با این اعداد بیان کنم. نخست اینکه بعضی از آنها خوب تعریف نشدهاند،
یا تعریف آنها ناقص است! البته این ”تعریف نشدن“ به کمکاری ریاضیدانی که آنها را
تعریف کرده باز نمیگردد، بلکه جزئی از ذات این اعداد است. دوماً، همانطور که ذکر
شد، این اعداد پاسخ مسائل خاصی (یا کرانههای خاصی) در منطق مراتب بالاتر هستند. و
نهایتاً اینکه ثابت شده که خیلی از آنها با توجه به تعریف بازگشتی (recursive) خودشان قابل محاسبه نیستند! (برای نمونه به
تابع Busy beaver،
یا بازی سگآبی سختکوش، رجوع کنید.)
برای این نوع اعداد کلاسهایی تعریف
شده که مرتبه محاسبهپذیری آنها را معین میکند. و برخی از آنها، مثل عدد گاردن، (فعلاً)
در مراتب بالا قرار میگیرند. حداقل کاری که درمورد این اعداد باید انجام داد
مقایسه بزرگی آنها است، وگرنه ادعای اینکه فلان عدد از فلان عدد بزرگتر است حرف
بیهودهای است، و این باید به طریقی ثابت شود.
همانطور که در بخش نخست این مقاله
اشاره کردم، برای معرفی یک عددِ جدیدِ بزرگ، صرفاً عدد سازی کافی نیست، وگرنه هر
عددی را که ذکر کنید، هر بچهای میتواند یک چیزی به آن اضافه کند، آن را در
چیزی ضرب کند، آن را به توان عدد دیگری برساند، یا اگر با عملیات ردههای بالاتر
(ابر-عملها) آشنا باشد، از آن عملیات برای بزرگتر کردن عدد قبلی استفاده کند. عدد جدید شما باید جواب یک مسئله فیزیک یا
ریاضی باشد و نباید صرفاً حاصل یک عدد سازی بچگانه باشد.
خیلی وقت
است که مسائل فیزیک نتوانستهاند عدد بزرگی را تولید کنند (به
این قسمت رجوع کنید). میماند مسائل ریاضی. ولی ظاهراً چند سالی است که
مسائل مطرح در حوزههای متداول ریاضیات (نظریه اعداد، ترکیبات، ...)، نیز
نتوانستهاند مسائلی را تولید کنند که جواب آنها اعداد بزرگتری باشند. شاید
مهمترین عددی که بر پایه یک مسئله ملموس ریاضی مطرح شده، عدد گراهام باشد که بیش
از 45 سال از عمر آن میگذرد. دراینصورت، این سئوال پیش میآید که بقیه اعدادی که
در سالهای اخیر مطرح شدهاند و گفته شده از عدد گراهام خیلی بزرگترند، از کجا
آمدهاند؟ به عبارت دیگر آنها جواب چه مسائلی هستند؟ پاسخ این است که بیشتر آنها
فرای ریاضیات هستند! مگر فرای ریاضیات هم چیزی وجود دارد که در آن اعداد مطرح
باشند؟ بلی وجود دارد، و آن بنیادیترین علم بشر، یعنی منطق (logic)، است. منطق پایه
ریاضیات است و اصلیترین رکن آن اعداد میباشد.
تعریف
خیلی از اعداد که جدیداً بعنوان عددِ بزرگ مطرح میشوند، براساس منطق(هایی) بنا
شده که تعمیمی از منطق کلاسیک هستند و منطق مراتب بالاتر (Higher-order logic) نامیده میشوند. با
توجه به ماهیت پیچیده این تعاریف، خیلی وقتها این سئوال مطرح میشود که آیا
اینها را باید جزئی از اعداد حساب کرد یا شبه-بینهایت؟ معلوم است که تعریف آنها
هر چقدر هم که ناملموس باشند، بازهم متناهی هستند، پس بینهایت نیستند. ولی خیلی
فنی، ناملموس، و حتی غیرقابل محاسبهاند.
برخلاف
اینها، عددی مثل عدد گراهام، هم جواب مسئلهای است که میتواند تجسم شود (البته
برای تجسم آن باید یک ابَر-مکعب را در نظر بگیرید که در یک ابَر-فضا قرار دارد که
تعداد ابعاد آن عدد گراهام است!)، و همچنین خود این عدد را میتوان تجسم کرد. درست
است که عدد گراهام برپایه ابر-عملهایی تعریف شده که مرتبه آنها خیلی، خیلی،...
زیاد است، ولی بااینحال شما میدانید که این عدد حاصل یک سری ابر-عملها است که در
64 لایه انجام میگیرند و در هر لایه نسبت به لایه قبلی خیلی، خیلی، خیلی ...
بزرگتر میشوند. اینجا صحبت بر سر ابر-عمل است. در برخورد اول ممکن است ابر-عملها
ناملموس بنظر برسند، ولی اگر خاصیت تکراری آنها روشن شود، با توجه به اینکه ما از
دوران دبستان با عملیات سادهای مثل جمع و ضرب آشنایی داریم، درک عملیات ردههای
بالاتر نیز برای ما ملموس و عادی میشود (جمع تکراری از شمارش یکهاست، ضرب
تکراری از جمعها ، توان تکراری از ضربها ، ابر-4 تکراری از توانها، ابر-5
تکراری از ابر-4ها و ... است).
برای نشان
دادن اعداد بزرگی که بر پایه منطق مراتب بالاتر مطرح میشوند، نمادگذاریهایی
که پیشتر به آنها اشاره کردیم کاربرد اندکی دارند. آنها برای اینکار از نمادگذاریهای
خاصی استفاده میکنند که حتی در میان ریاضیدانان غیر مرتبط نیز ناملموس است.
بعنوان
نمونه، من تعریفی که برای عدد رآیو ارائه شده را بدون ذکر توضیحی در زیر میآورم:
”عدد رآیو
عبارت است از: کوچکترین عددِ بزرگتر از هر عدد متناهی که با عبارتی در زبان نظریه
مجموعهها بیان شده باشد که در آن تعداد نمادها عدد گوگول (10100) یا کمتر باشد.“
ثابت شده
که این عدد از عدد گراهام خیلی بزرگتر است. ولی بدون اینکه به جزئیات و معنی تعریف
فوق بپردازیم، فقط میخواهیم ببینیم این عدد به چه چیزهایی میتواند مربوط باشد.
در تعریف فوق به ”عبارتی در زبان نظریه مجموعهها“
اشاره میکند، پس میدانیم که این عدد برخلاف عدد گراهام یا اعدادِ بزرگِ سنتی، با
نظریه مجموعهها مرتبط است. و نهایتاً از تعداد (10100) نماد (علامت) صحبت
میکند، پس ورودی آن (10100) است. البته برای این
عدد تعریف فورمولبندی شدهای نیز وجود دارد که با یک فرمول مرتبه-دو تعریف
میشود، که در آن [φ] فرمول
کدگذاری-گودل و s یک متغیر نسبت دهی است:
∀R {
{for any (coded) formula
[ψ] and any variable assignment t
(R( [ψ],t) ↔
( ([ψ] = `x_i ∈ x_j' ∧ t(x_1) ∈ t(x_j)) ∨
([ψ] = `x_i = x_j' ∧ t(x_1) = t(x_j)) ∨
([ψ] = `(∼θ)' ∧ ∼R([θ],t)) ∨
([ψ] = `(θ∧ξ)' ∧ R([θ],t) ∧ R([ξ],t)) ∨
([ψ] =
`∃x_i (θ)' and, for some an xi-variant t' of t,
R([θ],t'))
)} →
R([φ],s)}
اگر شما
جزء افرادی هستید که معنی عبارت فوق را نمیفهمید و علاقه دارید آن را درک کنید،
لازم است چند درس منطق ریاضی را بگذرانید.
منظور من
از مطرح کردن عدد رآیو اشاره به این واقعیت است که این مباحث و اعدادی که از آن
حاصل میشوند برای بیشتر افراد غیرقابل درک هستند. آنها به حوزههای پیشرفتهای از
منطق و ریاضیات وابسته هستند که نسبت به بقیه گرایشات ریاضی، دانشجویان کمتری به
آنها وارد میشوند، و حتی برای کسانی که در یکی از گرایشهای متداول ریاضیات (مثل
جبر، نظریهاعداد، توپولوژی، ...) فارغالتحصیل شدهاند نیز ناآشناتر هستند.
همانطور که بارها تاکید کردم، عدد بزرگی که
بعنوان رکورد دار اعداد بزرگ مطرح میشود، باید جواب یک مسئله باشد، شما نمیتوانید
از خودتان عدد در آورید و با ترکیب اعداد قبلی در یک عمل یا ابَر-عمل یا تابع، عدد
بزرگتری را حاصل کنید و بگویید عدد من از قبلی بزرگتر است. اگر میخواهید در
مواجهه با این نوع مسائل بطور سادهلوحانهای پیروز شوید و عددی را نام ببرید که
از همه اعداد بزرگی که قبلاً ریاضیدانان یا منطقدانان مطرح کردهاند بزرگتر باشد،
میتوانید بگوید عدد من الف-صفر (0א) است. ولی اولاً شما این عدد را اختراع نکردهاید
بلکه از اواخر قرن نوزدهم مطرح بوده، و دوماً، درست است که این عدد، و نظایر آن،
از هر عدد متناهی دیگری بزرگتر هستند، ولی اینها به حوزه اعداد نامتناهی یا
بینهایت تعلق دارند و شما مجاز به استفاده از این صلاحها نیستید! (به
کتاب مقدمه کوتاهی درباره بینهایت رجوع
کنید.)
و این ما را به ویژگی اصلی این اعداد، یعنی ”جواب یک
مسئله بودن“، میرساند. درست است که اعدادی که از اوایل قرن 21 بعنوان اعداد بزرگ
مطرح بودهاند، جواب یک مسئله هستند، ولی چه مسئلهای؟ آنها بسیار فنی هستند و
بجای اینکه حاصل مسائل ملموسی باشند، حاصل یک سری مسئلهسازی هستند. به عبارتی،
عددسازی بچگانه، جایش را به مسئلهسازی (تصنعی) داده. مسائلی که حاصل طبع بازیگوش
ریاضیدانان و منطق دانان هستند. در واقع عدد رایو حاصل یک مبارزه آکادامیک بین
ریاضیدان مکزیکی اگوستین رایو، و آدام الگا استاد دانشگاه پرینستون
بود. حتی در آن سال (2007) یک پُستر هم
برای آن منتشر شد که نمایانگر این چالش آکادامیک بود.

آگوستین رآیو (سمت چپ) و آدام الگا (سمت
راست).
اینکه آیا
نمونههای مذکور را میتوان جزئی از اعداد بزرگ محسوب کرد یا نه، هنوز جای مناقشه
دارد. ولی مورد مهمی که درباره این نوع اعداد وجود دارد این است که آیا آنها به
غیر از یک موضوع ریاضی بامزه، میتوانند کاربرد عملی نیز داشته باشند یا نه؟ مشکل
میتوان به این سئوال جواب داد. چیزی که بطور قطع میتوان گفت این است که اکثر
موضوعاتی که در ریاضیات مطرح شدهاند و در اوایل فقط جزء تفریحات ریاضی بحساب میآمده،
بعداً به طریقی در فیزیک یا علوم رایانهای جنبههای کاربردی پیدا کردهاند.
ریاضیدان
معروف بریتانیایی جی. اچ. هاردی زمانی گفته بود خوشحال است که حوزه نظریه
اعداد (که او متخصص آن بود) هیچ وقت در امور جنگی و نظامی کاربردی نخواهد
داشت، و مانند یک شعر زیبا، صرفاً یک موضوع ناب در ریاضیات باقی میماند. بعد از
جنگ جهانی دوم، و به فاصله چند سال از این اظهار نظر، با کوشش دانشمندانی مثل
تورینگ و شانون، رمزنگاری و مخابرات دیجیتال پاگرفت و ثابت شد که این گفته درست
نیست. بعد از آن هم دیری نپایید که علوم رایانهای، و به دنبال آن اینترنت گسترش
فراوانی پیدا کردند. اینها حوزههای هستد که پایه اصلی آنها را ریاضیات گسسته
تشکیل میدهد. رمزنگاری بدون استفاده از نظریه اعداد به چیز ضعیف و کم قدرتی بدل
میشود.
بنابراین
بعید نیست مطالعاتی هم که بر روی اعداد بزرگ صورت گرفته در آینده الهام بخش
کاربردهایی در فیزیک، علوم رایانهای، یا هر علم دیگری باشند که ما فعلاً از آن بیخبریم.
آیا کسی 60 سال قبل فکر میکرد تکنولوژی شبکههای کامپیوتری و مخابرات موبایل
اینقدر پیشرفت کند؟ اگر فیلمهای علمی-تخیلی دهههای 1950 یا 1960 را نگاه کنید،
چیزی که عمدتاً از آینده به شما نشان میدهند روباتهای زمختی هستند، که حتی به
آنها روبات هم نمیگفتند و به آدم آهنی معروف بودند. ظاهرِ روباتهای
امروزی نسبت به آنها خیلی انسانیتر و انعطافپذیرتر است. این یعنی ما نمیتوانیم
آینده را دقیق پیشبینی کنیم.
از قرن
هفدهم به بعد، بینهایت به ابزاری تبدیل شد که حالا تقریباً تمام علوم به آن
وابستهاند، زیرا بینهایت پایه حسابان است و کلیه علوم امروزی به حسابان وابستهاند.
بخاطر داشته باشید که اعداد بزرگ بینهایت نیستند، آنها عددند و کار با آنها از
جهاتی میتواند جالبتر باشد. از همین روی، اعداد بزرگ نیز میتواند پایه علوم
جدیدی باشد. علومی که برای تکنولوژیهای جدید بسترهایی را فراهم میآورند، چیزهایی
که ما حالا نمیتوانیم چگونگی آنها را پیشبینی کنیم.
اگر جنگهای
جهانی ویرانگر، بیماریهای همهگیر و غیرقابل علاج، یا تغییرات اقلیمی گسترده روی
ندهند، و بشر با همین سرعت به پیشرفت خودش ادامه دهد، بالاخره نوبتِ کاربردِ اعداد
بزرگ هم میرسد، اینکه کِی و چطور، این چیزیست که آینده مشخص میکند.
https://en.wikipedia.org/wiki/Large_numbers
https://en.wikipedia.org/wiki/Hyperoperation
https://en.wikipedia.org/wiki/Knuth%27s_up-arrow_notation
https://en.wikipedia.org/wiki/Graham%27s_number
https://en.wikipedia.org/wiki/TREE(3)
https://en.wikipedia.org/wiki/Rayo%27s_number