همان‌طور که از عنوان کتاب پیداست، این کتاب درباره تاریخ ریاضیات است و مهمترین موضوعات و اکتشافاتی که در طول 4 هزار سال در این حوزه پدید آمده را مورد بررسی قرار می‌دهد. با توجه به حجم نسبتاً اندک کتاب، در اینجا فقط به مهمترین اشخاص و موضوعات پرداخته شده. کتاب به 40 فصل بخش‌بندی شده، که حدود 10 فصل اول آن به ریاضیاتِ باستان (بابلی، مصری، یونانی و قرون وسطایی) مربوط است. بقیه فصول نیز به ترتیب زمانی، به بررسی ریاضیات مناطق دیگر جهان می‌پردازد (چین، خاورمیانه، هند، ژاپن، اروپا ...). مترجمِ کتابِ حاضر پیش از این نیز کتاب‌های دیگری را ترجمه کرده بود که به نوعی با تاریخ ریاضیات مرتبط بودند، مثلاً شخصیت‌های برجسته جهان ریاضیات، یا جهان شگفت انگیز اعداد، که هر دو توسط ریاضیدانِ مشهور انگلیسی یان استوارت (Ian Stewart) نوشته شده بودند. درباره کتاب حاضر تنها کافیست اشاره شود که خود استوارت از آن تمجید کرده و در توصیف آن گفته «اگر می‌خواهید یک مرور سریع و خواندنی از چند هزار سال تاریخ گذشته ریاضیات داشته باشید، چیزی بهتر از این کتاب به ذهنم نمی‌رسد.»

ولی این کتاب نسبت به کتاب‌های استوارت ویژگی‌های دیگری نیز دارد. یکی اینکه جدیدتر است، و به ریاضیات قرن بیست و یکم نیز پرداخته، و دیگر اینکه از دید یک ریاضیدانِ خانم نگاشته شده. از کسانی که در فصول آخر کتاب به آنها پرداخته شده، ترنس تائو، مارینا سرگیونا ویازوفسکا، و مریم میرزاخانی است، که همه ریاضیدانانی هستند که در دهه‌های پایانی قرن بیستم متولد شدند، ولی اوج شکوفایی آنها در قرن بیست و یکم بوده. هر سه آنها برنده بزرگترین افتخار ریاضی جهان، یعنی مدال فیلدز، شدند و به غیر از مریم عزیز ما، که خیلی زود پَرپَر شد، هر دو آنها هنوز فعالیت می‌کنند.

با داشتن کسانی مثل عمر خیام، غیاث‌الدین جمشید کاشانی، و محمد خوارزمی بعنوان ریاضیدانان ایرانی، حالا پس از گذشت حدود 1000 سال، جای بسی افتخار است که یک زن ریاضیدان ایرانی، یعنی مریم میرزاخانی، جای خود را در تاریخ ریاضیات باز کرده است. یادش همیشه گرامی.

درباره نویسنده

شِنه‌ژانا لارنس (Snezana Lawrence) ریاضیدان انگلیسی است. او در سال 1964 در یوگسلاوی متولد شد. تحصیلات ابتدایی و متوسطه خود را در آنجا به پایان رساند و با فروپاشی یوگسلاوی سابق، در اوایل دهه 1990 به انگلستان آمد، و در سال 2002 دکترای خودش را در رشته ریاضی گرفت. او در دانشگاه میدلسکس انگلستان تدریس می‌کند و تمرکز کاری او روی تاریخ ریاضیات است.

پاییز 1404
کامران بزرگزاد ایمانی

فصل 1

نقوش ریاضی

ریاضیات چه حسی را در شما برمی‌انگیزد؟ از نظر بسیاری از مردم، ریاضیات می‌تواند ترسناک باشد، زیرا خیلی سخت، خیلی سرد، و خیلی انتزاعی است. این حسِ ترس ممکن است از ابتدای دوران تحصیل در شما به وجود آمده باشد، به خصوص زمانی که کار با علامت‌ها، و انجام محاسبات، خیلی روشن نبودند. اگر اطرافیان شما در مورد دشوار یا بی‌معنی بودن ریاضیات صحبت می‌کنند، به احتمال زیاد شما هم همین فکر را خواهید کرد، پس شما می‌توانید این حس را به ارث برده باشید یا توسط دیگران به شما منتقل شده باشد. بنابراین، بسیاری از مردم به محض اینکه بتوانند، ریاضیات را کنار می‌گذارند. آنها می‌پرسند: «فایده ریاضیات چیست؟» و می‌گویند به نظر آنها ریاضیات به آن چیزهایی که می‌تواند در دنیای واقعی به آن نیاز داشته باشیم، ارتباطی ندارد.

با این حال، بعضی‌ها نیز چیزی شبیه به یک درک شهودی از ریاضیات را تجربه می‌کنند، و به مرور زمان آن را پرورش می‌دهند. بله، ریاضیات دشوار است، اما این اشخاص چنین چالشی را می‌پذیرند. آنها می‌توانند زیبایی‌هایی را در ریاضیات ببینند که دیگران (متأسفانه) نمی‌توانند آنها را ببینند. شاید آنها می‌خواهند شغلی داشته باشند که به دانش ریاضی نیاز داشته باشد. آنها عشق به این موضوع را در خود پرورش می‌دهند و از اینکه این رشته می‌تواند آنها را به کجاها برساند، هیجان‌زده می‌شوند.

چه از ریاضیات بترسید و چه شیفته آن باشید، تاریخ این حوزه نه تنها چهره متفاوتی از آن را به شما نشان می‌دهد، بلکه دقیقاً نشان می‌دهد که چگونه و چه زمانی کاربرد داشته است. همچنین نشان می‌دهد که گاهی اوقات ریاضیات چقدر می‌تواند زیبا باشد. همانطور که خواهیم دید، ریاضیات فقط درباره کار با اعداد نیست. ریاضیات در مورد توانایی کشف نوعی قانون کلی، و سپس نحوه اعمال آن در موقعیت‌های دیگر است. ریاضیات مهارت‌هایی را در شما پرورش می‌دهد که می‌تواند انواع مختلفی از مسائل را، چه ریاضی باشند و چه غیر ریاضی، حل کند. در این کتابِ موجز، شما با مروری بر تاریخ ریاضیات، بسیاری از نمونه‌های همه‌کاره بودن ریاضیات را خواهید یافت، نمونه‌هایی که از معادلات و حساب بسیار فراتر رفته، و از زمین به آسمان‌ها می‌رود.

شاید شما هم در جایی یک مطلب ریاضی را دیده، و درست آن را نفهمیده باشید. در اینمورد شما اولین نفر نیستید؛ مطمئن باشید حتی ریاضیدانان حرفه‌ای هم گاهی اوقات برای درکِ درستِ مسائلی که به آنها می‌پردازند، باید با همکاران خودشان گفتگو کنند. اما در وهله اول چگونه می‌توان تشخیص داد که یک نوشته نامفهوم یک مطلب ریاضی است؟ مثلاً یک سری نمادهای پیچیده می‌تواند به ذهن شما خطور کنند (مثلاً خطوط تیره، خطوط مورب و حروف عجیب). اینها همه نشانه‌های واضحی از ریاضیات هستند، همانطور که خواهیم دید، بسیاری از این علائم واقعاً جدیدند. اما مدت‌ها قبل از اختراع خطوط تیره و علائم پیچیده، باز هم ریاضیات وجود داشته است. به عبارت ساده، باید یک چیزِ ریاضی در جریان باشد تا بگوییم که این به ریاضیات مربوط است. اگر با یک دست‌نوشته روبرو شوید که به گذشته‌‌های بسیار دور تعلق دارد، و به زبانی نوشته که برای ما آشنا نیست، گاهی اوقات تشخیص اینکه آیا این نوشته‌ها ریاضی هستند یا نه، می‌تواند دشوار باشد.

این مشکلی بود که یک باستان‌شناس بلژیکی به نام ژان دو هاینزلین دو براکور (Jean de Heinzelin de Braucourt)، در دهه 1930 با آن مواجه شد. در آن زمان او به طور اتفاقی به گنجینه‌های باستانی در نزدیکی دریاچه ادوارد در ایشانگو ( Ishango) (که اکنون در جمهوری دموکراتیک کنگو قرار دارد) برخورد کرد. او در میان بقایای انسانی و ابزارهای سنگی، یک استخوان بابون نوک تیز پیدا کرد که تقریباً به اندازه یک مداد بود، و در کناره‌های آن حکاکی‌های عجیبی داشت. کاوش‌های بعدی در این محل شواهد بیشتری را کشف کرد، که شامل سلاح‌ها، نیزه‌ها، و حتی برخی طناب‌های قدیمی بود که ثابت می‌کرد اینجا مکانی بوده که گروهی از انسان‌های ماقبل تاریخ در آن زندگی می‌کردند. با این حال مدرک اصلی یافت شده، یعنی استخوان ایشانگو (Ishango bone)، تا مدت‌ها بعنوان یک معما باقی ماند. اما این استخوان چه بود؟

استخوان ایشانگو

168 حکاکی روی کناره‌های این استخوان عجیب به نظر می‌رسید، اما این نشان دهند چیزی بیش از یک شیء تزئینی صرف بود. اغلب اوقات، نیاز به حل مسائل از روی علائم یا نمادها، نشانه خوبی است که نشان می‌دهد با چه چیزی سر و کار داریم. و همینطور هم شد. استخوان ایشانگو به نوعی دستگاه ضبط یا شمارش تبدیل شد. کتیبه‌های روی این استخوان، نوعی عبارت ریاضی بودند. حکاکی‌ها در سه ستون موازی سازماندهی شده بودند که هر کدام روش متفاوتی را نشان می‌دادند. مثلاً دو برابر کردن مقادیر، فهرست کردن مقادیر اعداد اول بین 10 تا 20، و جمع کردن دو مقدار حول عدد 20. اعداد اول (Prime numbers) اعدادی هستند که فقط بر 1 و خودشان قابل تقسیم هستند، و همانطور که خواهیم دید، این اعداد برای اولین بار حدود 500 سال قبل از میلاد، یعنی قرن‌ها پس از استخوان ایشانگو، که در حدود بیست‌هزار سال پیش ساخته شده بود، تعریف شدند. البته، برخی ممکن است بگویند که این علائم صرفاً حاصل یک تصادف بوده‌، اما این حکاکی‌ها بیش از حد منظم هستند، تا اینکه نتیجه خط‌خطی‌‌های تصادفی کسی باشند. اکنون تا حد زیادی اعتقاد بر این است که استخوان ایشانگو اولین شیء ریاضی در تاریخ ریاضیات است که تاکنون کشف شده.

برای اینکه یک شیء را ریاضی بنامیم، چنین شیئی باید با یک تلاش انسانی ساخته یا شکل داده شده باشد، یا حاوی یک چیز ریاضی باشد، یا به آن اشاره کند. به معنای روزمره، ما استخوان ایشانگو، یک چرتکه، یا یک ماشین حساب را اشیاء ریاضی می‌دانیم. اما یک شیء ریاضی می‌تواند فقط ایده‌ای از یک شیء باشد. به عبارت دیگر، همه اشیاء ریاضی چیزهایی نیستند که بتوان مثل این استخوان آنها را لمس کرد. امروزه ریاضیدانان تمام مواردی را که می‌توانیم روی آنها عمل کنیم یا کاری با آنها انجام دهیم، اشیاء ریاضی می‌نامند. به عنوان مثال، نقطه‌ای مانند A، خطی مانند b، عددی مانند n، همگی می‌توانند اشیاء ریاضی باشند. اینها اشیاء انتزاعی (abstract objects) هستند: مثلاً وقتی ریاضیدانان به نقطه‌ای مانند A اشاره می‌کنند، به یک نقطه ریاضی با ویژگی‌های خاص (مثل موقعیت آن) اشاره می‌کنند، نه به یک نقطه واقعی در یک فضای واقعی.

بنابراین ممکن است به طور اتفاقی به اولین مشکل خودمان برخورده باشیم. یا شاید به درک اینکه یک شیء ریاضی چیست، نزدیک‌تر شده‌ایم. استخوان ایشانگو یک شیء انتزاعی نیست (یک چیز کاملاً واقعی است که می‌توان آن را دید و لمس کرد) اما آنچه در آن هست کاملاً انتزاعی است و به دانشی اشاره دارد که مطمئناً می‌توانیم آن را ریاضی بنامیم. حکاکی‌های منحصر به فرد آن، اولین سیستم شمارش از این نوع را نشان می‌دهد که توسط انسان ثبت شده. این همان چیزی است که این شیء را ریاضی می‌کند.

آیا ریاضیات مستقل از ما وجود دارد؟ قوانین و قواعد ریاضی به نحوی در طبیعت و جهان حک شده‌اند. به نظر می‌رسد رفتار برخی از حیوانات به شکل ریاضی‌ باشد: برای مثال، زاغچه‌ها می‌توانند تفاوت بین 5 و 6 شیء را تشخیص دهند؛ شامپانزه‌ها می‌توانند به این واقعیت که 5 بیشتر از 4 است، اشاره کنند. و نباید زنبورها که کندوهایی به شکل شش ضلعی‌های منظم می‌سازند، یا مورچه‌ها که به طور کامل قادر به تشخیص خروجی‌ها در فضاهای بسته هستند را فراموش کنیم. اما این توانایی‌های به ظاهر ریاضی، چیزی بیش از تشخیص، غریزه، و رفتار ذاتی نیستند. به عبارت دیگر، زنبورها بر اساس رفتار ریاضی خانه نمی‌سازند. آنها به طور کلی خانه‌های شش‌ضلعی خود را با ایده‌هایی در مورد بهترین روش چیدمان مرتبط نمی‌کنند (همانطور که خواهیم دید، این کار توسط یک ریاضیدان قرن بیستمی توضیح داده شد). بلکه این کاریست که فقط آن را انجام می‌دهند.

ما انسانها همیشه سعی می‌کنیم اوضاع را بهتر کنیم و وقتی موفق به انجام کارِ خوبی می‌شویم، همچنان به دنبال بهبود آن هستیم. گاهی اوقات این ما را به جاهایی می‌رساند که از آنچه تصور می‌کنیم، و با ریاضیات به آن ساختار می‌بخشیم، با واقعیت مطابق نیست. این با آنچه زنبورها، و تا آنجا که می‌دانیم با آنچه هر حیوان دیگری انجام می‌دهند، بسیار متفاوت است. بیش از دو هزار سال است که انسان‌ بر دانش خود در مورد شناخت الگوها و ارتباط آن با الگوهای دیگر تکیه کرده است. حالا ما به جای فضای سه بعدی که در آن زندگی می‌کنیم، می‌توانیم از ریاضیات برای در نظرگرفتن فضاهایی با ابعاد بسیار بیشتر استفاده کنیم. با استفاده از ریاضیات می‌توانیم در رفتارهای به ظاهر آشفته‌ای که در انواع مختلفی از زمینه‌ها، از طبیعت گرفته تا اقتصاد، رخ می‌دهند، پیش‌بینی‌هایی را انجام دهیم. ما چنان ساختارهای انتزاعی ریاضی بلند مرتبه‌ای را توسعه داده‌ایم که اگر روی آنها بایستید و از آن بالا به استخوان ایشانگو نگاه کنید، احساس سرگیجه خواهید کرد. ما همچنان بطور دائم در حال توسعه این ساختمان هستیم.

ما به برخی از چیزهایی که دو شاخه اصلی ریاضیات را تشکیل می‌دهند، یعنی ریاضیاتِ محض (pure mathematics) و ریاضیاتِ کاربردی (applied mathematics)، اشاره کردیم. در ریاضیات محض، ما به نتیجه‌گیری‌های انتزاعی می‌پردازیم. این نوع از ریاضیات شامل نظریه اعداد، هندسه، جبر، و آنالیز می‌شود که در ادامه این کتاب بیشتر در مورد همه آنها صحبت خواهیم کرد. ممکن است آن چیزهایی که در ریاضیاتِ محض یاد می‌گیریم، فوراً، یا حتی هیچ وقت، به طور مستقیم از آنها استفاده نکنیم. گاهی اوقات انسان قرن‌ها صبر می‌کند تا ببیند کجا می‌تواند به صورت عمَلی از ریاضیاتِ محض استفاده کند.

از سوی دیگر، ریاضیاتِ کاربردی معمولاً از مسائلی ناشی می‌شود که می‌خواهیم آنها را در زندگی واقعی خودمان حل کنیم. ما از چنین ریاضیاتی معمولاً در زندگی واقعی خودمان کم و بیش استفاده می‌کنیم. ریاضیات کاربردی با سئوالات و مسائلی سروکار دارد که از رشته‌های دیگر، مانند فیزیک، مهندسی، کامپیوتر، زیست‌شناسی، اقتصاد (و خیلی حوزه‌های دیگر) ناشی می‌شوند و همچنین در پیشرفت این رشته‌ها نقش دارد.

یک وجه مشترک ریاضیات محض و کاربردی، تدوین قوانین و نحوه تعمیم دادن آنهاست. ریاضیات کاربردی می‌تواند به درک الگوی حرکتِ نهنگ‌ها و رقص‌ مسحورکننده آنها در اقیانوس‌های پهناور کمک کند. در قیاس با این، ریاضیدانانِ محض مانند غواصانی در اعماق دریا هستند که صرفاً برای لذت بردن، خودشان را در دنیای جذاب ایده‌های محض غرق می‌کنند. اما حتی وقتی به نظر نمی‌رسد چنین دنیایی هیچ ارتباطی با تجربیات روزمره ما داشته باشد، آنها مشتاقِ توصیفِ قوانین و ساختارهای آن هستند. در طول تاریخ ریاضیات، هم در ریاضیات محض و هم در ریاضیات کاربردی، می‌توانیم چنین ماجراجویی‌هایی را دنبال کنیم، و در حیرت و شگفتی کشفِ آنها سهیم باشیم.

انسان همیشه در زمان‌ و مکان‌های مختلف متوجه چیزهای جدید شده و ایده‌های جدیدی ارائه داده، آنها را ثبت کرده، با آنها بازی کرده، و به این ترتیب ریاضیات جدیدی را خلق کرده است. این مانند زبان است: همانطور که ما می‌توانیم در خلق اشعارِ جدید، کلمات را به اراده خود تغییر دهیم، و یک ساختار زبانی کافی برای قابل فهم بودن اشعار خودمان تشکیل دهیم، به همین ترتیب می‌توانیم به طور مداوم از آنچه قبلاً به ارث برده‌ایم، ریاضیات جدیدی را بسازیم و ابداع ‌کنیم. این دلیل دیگری است که تاریخ ریاضیات مهم است، زیرا با نگاه به پیشرفت‌های پی در پی در این حوزه، می‌توانیم از محورهای حیاتی که ریاضیات بر آنها بنا شده و چرخش‌هایی که در مسیر توسعه خود داشته است، بیشتر بیاموزیم. می‌توانیم بین مردمانی که نه تنها از لحاظ مکانی، بلکه از لحاظ تاریخی از یکدیگر دور هستند، رقص پویای ایده‌های ریاضی را ببینیم. از طریق ریاضیاتی که انسانها خلق می‌کنند، گفتگوهای جهانی توسعه می‌یابد و مسائلی که قبلاً در یک دوره تاریخی مطرح شده بودند، می‌توانند در دوره دیگری حل شوند. ریاضیدانان همیشه با تکیه بر آنچه دیروز کشف شده است، به سؤالات امروز پاسخ می‌دهند.

بنابراین، با توجه به نقوش‌ ایجاد شده روی استخوان ایشانگو، برای سفری آماده شوید که در آن «نقوشِ‌ ریاضی» جذاب‌تری را بررسی خواهیم کرد که در طول قرن‌ها از فرهنگ‌های گوناگون برای ما به‌جا مانده است.

در طول این کتاب ما شگفت‌زده خواهیم شد که چگونه تکامل ریاضیات و تقویت مهارت‌های مختلف انسان در فرهنگ‌های مختلف موجب تزریق روش‌های جدیدِ تفکر در این رشته شده است. ما در این ماجراجویی تاریخی، نه تنها چنین ردپاهای ریاضی را کشف خواهیم کرد، بلکه خواهیم فهمید که منشأ اصلی آنها کجا بوده و زنان و مردانِ سراسرِ جهان چه سهمی در ریاضیات داشته‌اند.

حتی پیش پا افتاده‌ترین کارهایی که شما در زندگی روزمره خود انجام می‌دهید، ناگهان می‌توانند با نوعی جادوی ریاضی عجین شوند. وقتی به سوپرمارکت می‌روید، یک نکته ریاضی تاریخی ممکن است به شما در یافتن بهترین خرید کمک کند. وقتی در حال بودجه‌بندی حقوق ماهیانه خود هستید، ریاضیاتی که به دوره قرون وسطی تعلق دارد، به شما کمک می‌کند تا بهترین تصمیمات را بگیرید. اگر به انجام امور مالیاتی مشغول هستید، با استفاده از مقدارِ اندکی از دانش ریاضی، می‌توانید نتیجه مطلوب‌تری بگیرید. البته نمی‌توانم به شما قول بدهم، اما همه اینها ممکن است دیدگاه شما را نه تنها نسبت به ریاضیات، بلکه نسبت به جهان نیز تغییر دهد. شما می‌توانید در کشف الگوها و نتیجه‌گیرهای‌، به یک نابغه تبدیل شوید. ممکن است از درکِ ریاضیاتی که هرگز فکر نمی‌کردید بتوانید آن را بفهمید، احساس قدرت کنید. حتی ممکن است احساس کنید که یک قدرتِ خاص دارید، زیرا با داشتن دانش ریاضی، زیربنای بسیاری از مظاهر دنیای مدرن برای شما آشکار می‌شود. با مطالعه این کتاب، یک چیز قطعی است، و آن این است که شما قادر خواهید بود تاریخ اکتشافات ریاضی را درک کنید و امیدواریم از انجام رویه‌های ریاضی در زندگی روزمره خود لذتِ بیشتری ببرید.

اغلب گفته می‌شود که «ریاضیات زبان توصیفِ جهان است». بیایید زمان اندکی را صرف بررسی این زبان و روش‌های مختلفِ آن بکنیم. در طول تاریخ جهان، ما می‌توانیم خودمان را جای ریاضیدانانِ پیشین بگذاریم و ببینیم آنها چگونه دانشی که به ارث برده بودند را تدوین کرده و آن را گسترش دادند. با انجام این کار، آنها واقعیتِ زمانِ خودشان را اندکی تغییر دادند و آن را به واقعیتِ دنیای ما نزدیکتر کردند.

...........................................

محتویات کامل این کتاب در 40 فصل و 370 صفحه منتشر شده، برای ادامه مطالعه این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.

فصل 2

از زیرخاک درآوردن دانش

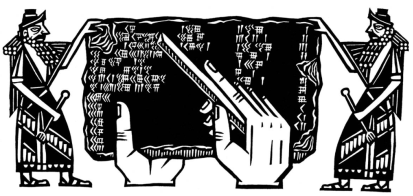
در سال 1922 یک ناشر و گردآورنده آمریکایی کتاب‌های قدیمی و عتیقه، به نام جورج آرتور پلیمپتون (George Arthur Plimpton)، یک لوح رُسی کوچک را به قیمت 10 دلار خریداری کرد. این لوح حاوی نوشته‌های مرموزی بود که در آن زمان فقط تعدادِ انگشت‌شماری از مردم جهان قادر به خواندن آن بودند. چه کسی در آن زمان فکر می‌کرد که این لوح کوچک به یکی از مشهورترین گنجینه‌های ریاضی تمام دوران تبدیل شود؟

پلیمپتون این لوح را که اکنون به نام خودش، پلیمپتون 322 نامیده می‌شود، از یک باستان‌شناس و ماجراجو به نام ادگار جی. بَنکس، خرید. بنکس، که کسی شبیه به ایندیانا جونز[1] بود، کنسول آمریکا در بغداد بود و بسیاری از این گنجینه‌های کوچک را از عراق و بازارهای قسطنطنیه می‌خرید تا به مجموعه‌داران ثروتمندِ کشورهای اروپایی بفروشد. شاید او پیش خودش فکر می‌کرد که قیمت خوبی برای این لوح، که به اندازه یک کارت پستال بود، گرفته است، اما امروزه از لحاظ اهمیت تاریخی، نمی‌توان روی این لوح قیمتی گذاشت. زیرا بخش زیادی از آنچه ما در مورد ریاضیاتِ بین‌النهرینِ باستان می‌دانیم از کشف این شیء کوچک ناشی می‌شود.

لوح پلیمپتون 322

این لوح با ارتفاع 9 سانتی‌متر، عرض 13 سانتی‌متر، و ضخامت 2 سانتی‌متر، حدود 1800 سال پیش از میلاد مسیح ساخته شده و احتمالاً در جایی در جنوب عراق امروزی پیدا شد. این لوح مملو از نوشته‌هایی به خط میخی است. نوشته‌هایی در چهار ستون حکاکی شده‌اند. اگر آن را مانند یک کتاب انگلیسی، از چپ به راست بخوانید، متوجه خواهید شد که ستون اول دارای فهرستی از اعداد است که به ترتیب نزولی فهرست شده. این اعداد رابطه خاصی با دو عدد دیگر در همان ردیف دارند. اما اگر آن را از راست به چپ، مانند زبانهای عبری یا عربی، بخوانید، ستون اول به فهرستی از اعداد ترتیبی (اول، دوم، سوم و غیره) تبدیل می‌شود که هر ردیف را مشخص می‌کنند. از کجا می‌دانیم که اینها عدد هستند؟ مدت‌ها بود که کسی از این موضوع اطلاع نداشت، زیرا قرن‌ها بود که زبانهای دوران بین‌النهرین منسوخ شده بودند. ولی خوشبختانه، زمانی که لوح به ایالات متحده آورده شد، این زبانها دوباره کشف شدند و می‌شد آنها را رمزگشایی کرد.

تمدن‌های بین‌النهرین، شامل سومری‌ها، آشوری‌ها، اکدی‌ها و بابلی‌ها، از لحاظ جغرافیایی توسط دو رودخانه بزرگِ دجله و فرات، تعریف می‌شدند و در دوره 3100 تا 540 پیش از میلاد شکوفا شدند. این دوره 3000 ساله، دورانی طولانی است، این مدت طولانی‌تر از کلِ زمانی است که از زمان نابودی آنها تا امروز گذشته. با توجه به مدت زمانی که این تمدن‌ها پابرجا بوده‌اند و اینکه سایر تمدن‌های باستانی چقدر برای ما ناشناخته هستند، آنچه در مورد مردمان بین‌النهرین باستان می‌دانیم تا حدودی اندک است. همچنین بسیار شگفت‌آور است که دستاوردهای آنها تا اواسط قرن نوزدهم عمدتاً ناشناخته بود، زیرا کتیبه‌هایی که این دست‌آوردها را توضیح می‌دادند، غیرقابل خواندن بودند.

خط میخی که در بین‌النهرین اختراع شد، در واقع قدیمی‌ترین خطی است که ما شواهدی از آن در تاریخ جهان داریم. مانند خط لاتین که بعدها ابداع شد، در این دوره نیز خط میخی در فرهنگ‌های مختلف، با زبانهای مختلف، در سراسر این منطقه وسیع توسعه یافت و مورد استفاده قرار گرفت. هنگامی که محققان شروع به رمزگشایی کتیبه‌های بین‌النهرین کردند، متوجه شدند که مبنای غالبی که برای شمارش و محاسبه از آن استفاده می‌شد، عدد 60 بود که به آن سیستم شصتگانی (sexagesimal) می‌گویند. در واقع ما هنوز هم برای اندازه‌گیری زمان از این سیستم استفاده می‌کنیم. در بین‌النهرین باستان بود که روز به 24 ساعت، هر ساعت به 60 دقیقه و هر دقیقه به 60 ثانیه تقسیم ‌شد، و حالا بیش از 4000 سال است که این سیستم پابرجا مانده. در ریاضیات، هنگام اندازه‌گیری زاویه‌ها نیز ما از همین سیستم استفاده می‌کنیم. یک دایره به 360 درجه، یک درجه به 60 دقیقه قوسی، و یک دقیقه به 60 ثانیه قوسی تقسیم می‌شود.

بیایید لوحِ کوچک پلیمپتون 322 را با جزئیات بیشتری بررسی کنیم. بر روی آن اعدادی در چهار ستون نوشته شده‌اند. این اعداد باید از راست به چپ و با شروع از شماره ردیف خوانده شوند. سه عدد باقی مانده در هر ردیف به یکدیگر مرتبط هستند. آنها سه مقدار مربوط به مثلث‌های قائم‌الزاویه را نشان می‌دهند. ممکن است از خود بپرسید چطور ممکن است؟ همانطور که می‌دانیم، و کاتبِ کتیبه پلیمپتون 322 نیز می‌دانست، در یک مثلث قائم‌الزاویه، مربعی که می‌توانید روی طولانی‌ترین ضلع آن (یعنی وتر) رسم کنید، برابر با مجموع مربع‌های دو ضلع دیگر خواهد بود. این قضیه اکنون قضیه فیثاغورث نامیده می‌شود که به افتخار ریاضیدان یونانی که در فصل 4 با او ملاقات خواهیم کرد، نامگذاری شده است.

بنابراین می‌توانید از هر یک از ویژگی‌های چنین مثلثی (طول اضلاع آن، یا مساحت مربع‌های ساخته شده روی اضلاع آن، یا هر نسبتی بین این طول‌ها و مساحت‌ها) برای پیدا کردن سه مقداری که به مثلث قائم‌الزاویه اشاره دارند، استفاده کنید. به زودی خواهیم دید که چگونه مجموعه‌ای از این اعداد در هر ردیف سازماندهی شده‌اند. اما جدا از ارائه اندازه‌هایی که در این لوح ذکر شده و می‌توانیم با آنها مثلث‌های قائم‌الزاویه بسازیم، ابتدا باید نگاهی به ریاضیات بیندازیم تا بفهمیم که چرا این لوح بسیار مهم و منحصر به فرد است.

ما با اعداد اول شروع می‌کنیم. اینها اعدادی هستند که فقط بر خودشان و 1 بخش‌پذیرند. هر عدد صحیح را می‌توان به صورت حاصلضرب عوامل اول آن بیان کرد. عامل اول یک عدد، عددی است که می‌تواند آن عدد را بدون باقیمانده تقسیم کند. برای دیدن اینکه ببینیم این کار چگونه انجام می‌شود، بیایید عدد 72 را در نظر بگیریم. شما می‌توانید این عدد را به عوامل اولش تجزیه کنید و آن را به صورت حاصلضرب عوامل اولش بنویسید: 2×2×2×3×3=72 یا 2³×3²=72. گاهی اوقات اعداد اول به عنوان بلوک‌های سازنده‌ اعداد شناخته می‌شوند. این بدان معناست که با یافتن عواملِ اولِ اعدادِ صحیح، می‌توانیم تمام آنها را به بلوک‌های سازنده‌شان تجزیه کنیم.

اعداد خاصی وجود دارند که مقسوم‌علیه‌های اول آنها فقط 2، 3 و 5 هستند. به چنین اعدادی، شصتگانی باقاعده (regular sexagesimal) می‌گویند. یک عدد شصتگانی باقاعده، مقسوم‌علیه هر عددی است که توانی از 60 باشد (مثلاً 60×60=3600). مقسوم‌علیه یک عدد می‌تواند آن عدد را بدون اینکه باقیمانده‌ای داشته باشد تقسیم کند. به عبارت دیگر، مقسوم‌علیه یک عدد، یکی از عوامل آن عدد نیز هست. این بدان معنی نیز هست که شما می‌توانید 60 را به توان هر عددی برسانید، و خواهید داید که حاصل آن بر 2، 3 و 5 (و توان‌هایی از این اعداد) بخش‌پذیر خواهد بود. کاتب لوح پلیمپتون 322 نگفته بود که همه این‌ها را می‌داند، اما مطمئناً از چنین چیزی استفاده کرده بود. دلیلش این است که در این لوح همه اعدادِ دو ستونِ وسط، اعداد شصتگانی باقاعده هستند. به عبارت دیگر، می‌توانید آنها را فقط با ضرب توان‌های اعداد اولِ 2، 3 و 5 بسازید. دو عدد وسط در تمام ردیف‌های لوح نیز به هم مرتبط هستند: یکی نشان دهنده طول ضلع کوتاه‌تر یک مثلث قائم‌الزاویه و دیگری وتر آن است. ستون آخر (از راست، یا اول از چپ) نسبت مربع‌های این دو ضلع است.

با توجه به اینکه ما شواهد زیادی از ریاضیاتِ ماقبلِ این لوح نداریم، و اثبات آنچه که اکنون قضیه فیثاغورث نامیده می‌شود نیز قرن‌ها بعد به دست آمد، این لوح واقعاً شگفت‌انگیز است.

اگرچه احتمالاً پلیمپتون 322 مشهورترین لوح است، اما تنها لوحی نیست که در دست داریم و بینشی از ریاضیات بین‌النهرین به ما ارائه می‌دهد. لوح‌های دیگری از این دوره، که دوره بابل قدیم نامیده می‌شود، و تقریباً یک بازه دویست ساله بین 1800 تا 1600 قبل از میلاد را پوشش می‌دهند، جداولی از نتایج را نشان می‌دهند که در صورت نیاز می‌توانستند در محاسبات مورد استفاده قرار گیرند – مثلاً شاید برای ساختن مثلث‌های قائم‌الزاویه یا دانستنِ نسبتِ مساحتِ مربع‌ها در چنین مثلث‌هایی.

ریاضیدانان بین‌النهرین در ساخت جداولی که در آنها فهرستی از اعداد با عملیات تکراری یکسان انجام، و نتایج حاصل از آنها را نمایش می‌دهند، بسیار ماهر بودند. ما لوح‌های گلی دیگری با جداول ضرب، جداول تقسیم، و جداول معکوس پیدا کرده‌ایم. عددِ معکوس عددی است که وقتی در عدد اصلی ضرب می‌شود، حاصل آن 1 می‌شود (برای مثال، 2 ضربدر مساوی با 1 است، بنابراین معکوس 2 است). لوح‌های بین‌النهرینی وجود دارند که اعداد و معکوس‌های آنها را در کنار یکدیگر نشان می‌دهند تا در محاسبات راحت‌تر بکارگرفته شوند. بین‌النهرینی‌ها همچنین می‌دانستند که چگونه جذر یک عدد را بدست آورند (یعنی عددی که وقتی در خودش ضرب می‌شود حاصل آن عدد اصلی است). امروزه این مهارت تقریباً فراموش شده، زیرا ما عمدتاً از ماشین حساب برای محاسبه جذر استفاده می‌کنیم، اما انجام آن با دست شامل مجموعه‌ای از محاسبات است که حاصل آنها به جذر مورد نظر نزدیک‌ و نزدیک‌تر می‌شود. از آنجایی که این محاسبه شامل عمل‌های تکراری زیادی است، تکمیل دستی آن می‌تواند زمان زیادی طول بکشد. بنابراین، داشتن جدولی از جذرهای از پیش محاسبه‌شده‌ از اعداد خاص بسیار مفید است. در برخی از منابع، طریقه به دست آوردن جذر اعداد به یک ریاضیدان یونانی بسیار متاخرتر، بنام هرون اسکندرانی (Heron of Alexandria) (حدود قرن اول یا دوم پیش از میلاد) نسبت داده می‌شود. اما در جداول بین‌النهرینی قدیمی هیچ فرمول صریحی برای اینکار ارائه نشده است و ما نحوه‌ی به دست آوردن این نتایج تکراری و چگونگی استنباط آنها را نداریم. به طور کلی، این یکی دیگر از ویژگی‌های اصلی ریاضیاتِ بین‌النهرین است: ما می‌دانیم که آنها می‌دانستند چگونه کارها را انجام دهند، اما نمی‌دانیم چگونه این کار را می‌کردند. آنها هیچ اثباتی برای نشان دادن نحوه‌ی کار یا چرایی انجام کارهای خودشان به جا نگذاشتند.

اعتقاد بر این است که اکثر لوح‌های گلی این دوره (که انبوهی از آنها در عراق امروزی پیدا شده‌اند) از مدارس آن دوره، یا مطمئناً از نوعی گروه‌های دانش‌آموزی سرچشمه گرفته‌اند. بسیاری از مسائل ریاضی به جای اینکه مانند آنچه حالا توسط نمادها مطرح می‌شوند، در آن زمان با کلمات مطرح می‌شدند و تقریباً همیشه هدف آنها به دست آوردن یک عدد بود. برخلاف ریاضیات دوره‌های بعدی، که از دانش‌آموزان خواسته می‌شد چیزی را اثبات کنند، مسائل لوح‌های گلی آن دوره، سؤالات خاصی را در رابطه با نوعی اندازه‌گیری مطرح می‌کردند. بنابراین در آنها سؤالاتی در مورد نحوه محاسبه طول یک کانال، مساحت مزارع، یا تعداد آجرهای مورد استفاده در ساخت و سازها پیدا می‌کنیم. وجود پاسخ‌ به این سئولات به ما می‌گوید که در آنجا نوعی یادگیری در جریان بوده، و به همین دلیل است که نتیجه می‌گیریم که بیشتر این لوح‌ها از نوعی مدرسه سرچشمه می‌گیرند.

از آنجایی که بسیاری از این مسائل به وضعیت‌های زندگی واقعی مربوط هستند، درک واحدهای اندازه‌گیری بسیار مهم است. ما می‌دانیم که سیستم شصتگانی بین‌النهرین عموماً به این معنی است که واحدهای مختلف آنها، کسور ساده یا مضرب‌هایی از 60 هستند و می‌توانیم آن را به سیستم متریک خودمان ترجمه کنیم. بنابراین مثلاً، کوچکترین واحد اندازه‌گیری شه (طول دانه جو) بود، که تقریباً برابر با متر است. اما در کل با نگاهی به ریاضیات بین‌النهرین، محاسبه واحدهای اندازه‌گیری مورد استفاده در هر مقطع خاص به هیچ وجه کار آسانی برای ما نیست. سیستم‌های اندازه‌گیری بین‌النهرین باستان بسیار پیچیده بودند و ناگزیر در طول دوره تمدن‌های مختلف تغییر کردند. تنها با نگاهی به دوره نسبتاً محدودِ بابلِ قدیم (که جالب‌ترین و پیچیده‌ترین ریاضیاتِ باستان از آن سرچشمه می‌گیرد) تنوع بسیار غنی از واحدها را می‌بینیم.

متأسفانه، با وجود تمام لوح‌های گلی که تاکنون کشف شده‌اند، هنوز نمی‌دانیم چه کسی آنها را ساخته یا نوشته است. ما حتی نمی‌توانیم بگوییم که آیا هیچ یک از نویسندگان آنها کسانی بوده‌اند که ریاضی می‌دانسته‌اند، یا صرفاً کاتب، دانش‌آموز، یا حتی معلم بوده‌اند. مطمئناً برخی از این لوح‌ها یافته‌های بدیعی را نشان می‌دهند (اینکه اولین باری کسی چیز مهمی را نوشته، و سپس دیگران آن ثبت کرده‌اند). می‌توانیم حدس بزنیم که در فرهنگ‌های بین‌النهرین، غالباً از ریاضیات استفاده می‌شده، زیرا لوح‌های زیادی مانند پلیمپتون 322 وجود دارد - به نظر می‌رسد افراد زیادی بودند که ریاضیات را مطالعه می‌کردند و می‌دانستند چگونه در عمل آن را به کار گیرند. با نگاهی به ادبیاتِ بین‌النهرینِ باستان، می‌توانیم تشخیص دهیم که مردم آن گاهی پرشور، شجاع، و بسیار شوخ‌طبع بوده‌اند.

بین‌النهرینی‌ها اولین خط نوشتاری، اولین جداول برای سرعت بخشیدن به محاسبات، و اولین روش اندازه‌گیری زمان را به ما دادند. آنها روش محاسبه چیزها را به یکدیگر نشان می‌دادند، اما ثابت نمی‌کردند که چرا یا چگونه این روش‌ها کار می‌کنند. این کار مهم بر عهده یونانیان بود ، یعنی همان تمدن باستانی که به زودی با آن آشنا خواهیم شد، ولی پیش از آن، سری به مصرِ باستان خواهیم زد.

فصل 3

داستان یک کاتب

پاپیروسی که حدود سال 1858 در خرابه‌های پر گرد و خاک تیبز (Thebes) کشف شد، احتمالاً به معروف‌ترین و ارزشمندترین اثر هنری تاریخ ریاضیاتِ مصر تبدیل شد. یک عتیقه‌شناس و جهانگرد، به نام هنری رایند (Henry Rhind)، چند سال قبل از مرگش آن را خرید و پس از فروش آن به موزه بریتانیا، این پاپیروس به نام او نامگذاری شد.

پاپیروسِ رایند، به همراه یک طومار چرمی که آن هم توسط او خریداری شده بود، و چند پاپیروس دیگر (که یکی از آنها در مسکو است) و چند لوح چوبی، تقریباً تمام اشیاء تاریخی هستند که به ما رسیده و شواهد مستقیمی از ریاضیاتِ مصریان باستان در طول تمدن طولانی و پربار سه هزار ساله آنها را ارائه می‌دهند. نیازی به گفتن نیست که دانش ما از ریاضیات مصری بسیار محدود است، و شاید جای تعجب نباشد که این دوره اغلب توسط مورخان ریاضیات نادیده گرفته می‌شود. اما اگر مصریان از نظر ریاضی ماهر نبودند، پس چگونه می‌توانستند چنین معماری باشکوهی (مثل اهرام شگفت‌انگیز) را بسازند؟ ما فقط می‌توانیم نگاهی اجمالی به آنچه که می‌تواند درک یک ریاضیدان باهوش از مهندسی، ساخت و ساز، و طراحی بوده باشد، بیندازیم.

با این وجود، برای قرن‌ها دانشمندانِ جهان توانایی خواندن هیروگلیف‌های مصری را نداشتند. زمانی که مصر توسط آشوری‌ها (671 پیش از میلاد)، ایرانیان (525 پیش از میلاد) و سرانجام سلسله بطلمیوسی یونانی (332 پیش از میلاد) فتح شد، چیز زیادی از فرهنگ اصلی آن باقی نمانده بود. در اواخر دوران مصر باستان، در کنار خطوط مصری، از خطوط یونانی و دموتیک (demotic) استفاده می‌شد، و زمانی که رومی‌ها به عنوان تمدنِ غالب در مدیترانه جایگزین یونانی‌ها شدند، هیروگلیف‌ها عمدتاً فقط توسط کاهنان مصری استفاده می‌شدند. در اوایل قرن نوزدهم بود که در نزدیکی شهر اسکندریه مصر، سنگ روزتا[2] (Rosetta Stone) پیدا شد. بعد از آن بود که یک زبان‌شناس فرانسوی توانست خط هیروگلیف را رمزگشایی کند، و سرانجام خواندن متون ریاضی مصری و تحلیل آنها آغاز شد.

...........................................

فصل 4

اسرار فیثاغورثیان

حتی اگر تقریباً هیچ چیز در مورد تاریخ ریاضیات ندانید، به احتمال زیاد نام فیثاغورث (Pythagoras) را شنیده‌اید. خارج از محافل ریاضی، احتمالاً او معروف‌ترین ریاضیدان است. اما ما واقعاً در مورد او چه می‌دانیم؟ ما می‌دانیم که او حدود 570 پیش از میلاد در جزیره یونانی ساموس متولد شد و حدود 495 پیش از میلاد در مگنا گراسیا (جنوب ایتالیای فعلی) درگذشت. فیثاغورث در جوانی سفرهای زیادی به مصر و سایر نقاط آفریقا، بابل، و احتمالاً هند انجام داد. او از هر مکانی که بازدید می‌کرد، چیزهایی یاد می‌گرفت، اما ما دقیقاً مطمئن نیستیم که چه چیزهایی.

از حدود سال 530 پیش از میلاد، فیثاغورث در کروتون زندگی می‌کرد، و در آنجا یک فرقه ریاضی غیرمعمول تأسیس کرد (که احتمالاً تنها نمونه‌ از آن در تاریخ بشر است). اعضای آن نه تنها ریاضیات را یاد می‌گرفتند و به یکدیگر آموزش می‌دادند، بلکه در نوعی جامعه اشتراکی با هم زندگی می‌کردند. نام‌ برخی از آنها در تاریخ آمده: هیپاسوس (Hippasus) (حدود 530-450 پیش از میلاد)، فیلولائوس (Philolaus) (حدود 470-385 پیش از میلاد) و آرخوتاس(Archytas) (حدود 435-360 پیش از میلاد). این گروه همچنین شامل زنان ریاضیدانان ، از جمله همسر خود فیثاغورث، تیانو (Theano)، و دخترشان، میا (Myia)، بود. اخیراً، مورخان منابعی را کشف کرده‌اند که حداقل نام هفده زن فیثاغورثی را در آنها ذکر شده. این افراد به این دلیل مورد توجه قرار می‌گرفتند که از نظر سهم‌شان در این گروه، مهم بودند. به عبارت دیگر، مطمئناً زنان بیشتری در این فرقه حضور داشتند. بنابراین برای اولین بار می‌توانیم از اولین زنان ریاضیدان نام ببریم، اگرچه دقیقاً نمی‌توانیم بگوییم که سهم آنها در توسعه ریاضیات فیثاغورثی چه بوده است.

فیثاغورث

مجمع فیثاغورثیان جالب، و بسیار پنهان‌کار، بود. اعضای این حلقه موظف بودند دانش خود را (که همانطور که خواهیم دید، شامل نیز ریاضیات بود) برای اشخاصِ خارج از حلقه فاش نکنند.

...........................................

فصل 5

پرفروش‌ترین کتابِ ریاضی تمام دوران

بهترین دانشمندان یونانِ باستان، به همراه جالب‌ترین اشیاء آن دوران، و تقریباً هر کتابی که در آن زمان وجود داشت، در موزه باشکوه موسیون (Mouseion) در اسکندریه مصر یافت می‌شد. این موزه که حدود قرن سوم پیش از میلاد توسط جانشین اسکندر کبیر، بطلمیوس اول و پسرش تأسیس شد، بهترین دانشمندان آن زمان را برای حفظ و یادگیری موضوعات مختلف گرد هم آورده بود.

گفته می‌شود که بطلمیوس اول مدت کوتاهی پس از پادشاه شدنش در مصر، اعلام کرد که می‌خواهد ریاضیات یاد بگیرد. او از کتاب‌های موجودِ راضی نبود؛ روی پاپیروس‌های مختلف، مطالب زیادی بصورت پراکنده نوشته شده بود، و مباحث ریاضی موجود در آنها بی‌ربط بودند و زیاد جالب به نظر نمی‌رسیدند. آیا کس دیگری می‌توانست ریاضیات را به روشی آسانتر و جذابتر به او بیاموزد؟ دانشمندان اسکندریه تلاش کردند تا برای جلب رضایت حاکم خود راه حلی پیدا کنند. آنها چگونه می‌توانستند تمام دانشِ ریاضی موجود را که در کتاب‌های مختلف در سراسر قلمرو وسیع آنها پراکنده بود، سازماندهی کنند؟ ناگهان فکری به ذهن کسی خطور کرد: در آن زمان ریاضیدانی به نام اقلیدس (Euclid) بود که به عنوان یک معلم درخشان معروف شده بود. او را به اسکندریه آوردند تا چنین کتابی را بنویسد.

اقلیدس

ما اطلاعات زیادی در مورد خودِ اقلیدس نداریم. حتی سال تولد و مرگ او نیز مشخص نیست؛ تصور می‌شود که او بین حدود 325-320 پیش از میلاد، تا حدود 280-265 پیش از میلاد زندگی می‌کرده است.

...........................................

فصل 6

پس اثبات‌ کجاست؟

افسانه‌های چینی می‌گویند که چگونه هوانگ دی (Huang Di)، که امپراتور زرد و نیای مقدس مردم چین نامیده می‌شد، در قرن بیست و ششم پیش از میلاد به شخصی به نام لی شو دستور داد تا علم حساب را اختراع کند. این در کنار دستوری بود که به یکی دیگر از وزرای او داده شد تا اولین سیستم نوشتاری چین را ابداع کند، بنابراین این امر تا حدودی نشان‌دهنده‌ قدمت علاقه‌ چینی‌ها به ریاضیات، و همچنین احترام بالایی است که ریاضیات در طول تاریخ چین داشته است.

سلسله هانِ متأخر (25-220 میلادی ) دوره‌ای بود که در آن مرزهای کشور چین، آنطور که امروزه هستند، تعیین شدند. همچنین در این دوره بود که جیوژانگ سوانشو، یا کتاب ”نه فصل در هنر ریاضی“، برای اولین بار منتشر شد. این کتاب همچنان مشهورترین رساله ریاضی است که از چینِ باستان سرچشمه گرفته. محققان غربی آن را با اصول اقلیدس مقایسه می‌کنند، اما کتاب ”نه فصل“ یک اثر بسیار متفاوت و بدیع بود. این کتاب به طور خاص بر مسائلی متمرکز بود که اثبات آنها به هیچ وجه با اثبات‌های کتاب اصول اقلیدس یکسان نیست.

محتوای کتابِ نه فصل در طی چندین قرن گردآوری شده است، و خود کتاب هم احتمالاً در قرن دوم یا اول پیش از میلاد نوشته شده است. ریاضیدانی به نام لیو هوی (Liu Hui) (حدود 225-295 میلادی)، که در سال 263 میلادی تفسیری بر این کتاب نوشت، گفته بود که نسخه اصلی بسیار قدیمی‌تر است. این رساله بر اساس متون باستانی، مانند سوان شو شو (نوشته‌هایی در باب حساب)، از مقبره‌ای که در قرن دوم پیش از میلاد مهر و موم شده بود، نوشته شده است، اما نه فصل بسیار بهتر سازماندهی شده بود، نظامند‌تر و طیف مسائل آن بسیار گسترده‌تر بود. این رساله از اصلاحات آموزشی کیوم شی هوانگ، بنیانگذار سلسله چین، که در حدود سال 213 پیش از میلاد دستور نابودی اکثر کتاب‌های قدیمی موجود، از جمله تمام کتاب‌های مربوط به ریاضیات را صادر کرد، جان سالم به در برد. محتویات این کتاب، به نحوی، در حدود سال 170 میلادی ذخیره و بازسازی شدند.

...........................................

فصل 7

طلوع نظریه اعداد

«اینجا مردی به نام دیوفانت آرمیده.» این آغاز یک معمای عجیب درباره بزرگترین ریاضیدان اواخر دوران باستان به نام دیافانتوس (Diophantus) است. او اهل اسکندریه، یعنی همان شهر زیبای یونانی واقع در دلتای نیل بود که در قرن سوم زندگی می‌کرد. زندگی او چگونه بود و چند سال عمر کرد؟ معمای زیر سن او را به ما می‌گوید. روشی که از طریق آن این کار را انجام می‌شود به این نکته اشاره دارد که چرا دیوفانتوس برای ریاضیات بسیار مهم بود. بیایید به این قطعه کوچک و جالب که سه قرن پس از مرگ دیوفانتوس، توسط ادیبی به نام مترودوروس نوشته شده است نگاهی بیندازیم:

خداوند یک ششم عمرش را به دوران کودکی‌اش بخشید،

در حالی که ریش و سبیل‌ها او زیاد شده بود، یک دوازدهم عمر او هم در جوانی گذشت؛

و سپس یک هفتم از زندگی او گذشت که دوران ازدواج آغاز شد؛

پنج سال بعد، پسری سرزنده و شاداب به دنیا آمد.

افسوس، فرزند عزیزِ استادِ فرزانه، پس از آنکه نیمی از عمر پدرش را گذراند، به سرنوشت بدی دچار شد.

پس از آنکه چهار سال با علم اعداد به زندگی خود تسلی داد، او به زندگی خود پایان داد.

بنابراین دوران کودکی دیوفانتوس یک ششم عمرش را در بر می‌گیرد؛ پس از یک هفتم دیگر ازدواج می‌کند؛ ریش او پس از یک دوازدهم دیگر عمرش رشد می‌کند؛ پسرش پنج سال پس از آن به دنیا می‌آید؛ پسرش تا نصف سن پدرش زندگی می‌کند؛ و دیوفانتوس چهار سال پس از مرگ پسرش می‌میرد.

...........................................

فصل 8

منشأ عدد صفر

از زمانی که اعداد برای اولین بار اختراع، و استفاده از آنها شروع شد، این درک وجود داشته که جایی در میان این اعداد چیزی متضاد با آنها وجود دارد، و آن نوعی هیچی، پوچی، یا یک فقدان کمیت است. حالا ما این عدد را صفر می‌نامیم و در خیلی از زبانها آن را با 0 نشان می‌دهند. اما صفر همیشه به عنوان یک عدد در نظر گرفته نمی‌شد. مفهوم صفر مدت‌ها قبل از این نام و علامت 0 وجود داشته است. ولی در هزاره اول، و در هند بود که این کمیتِ تهی به عنوان یک چیز ریاضی رسمیت پیدا کرد.

فرهنگ هند سابقه طولانی در ریاضیات دارد. سولباسوتراهای (Sulbasutras) قرن ششم هند، یک سری متون هندسی هستند که جزئیات چیدمان صحیح آجرها برای ساخت محرابِ‌ آیین‌های مذهبی را شرح می‌دهند، که قدمت آن به 1500 سال قبل از میلاد مسیح برمی‌گردد. در اینجا قضیه فیثاغورث ظاهر می‌شود (هرچند معلوم است که به نام آن ریاضیدان یونانی نامگذاری نشده بود)، ولی هنوز اثری از صفر نبود. فرهنگ‌های دیگر، مانند مایایی، بین‌النهرینی، و یونانی، روش‌هایی برای چگونگی کار با صفر داشتند، اما این شامل استفاده از یک عدد برای آن نبود. در عوض، آنها از یک جا‌نگه‌دار (placeholder) استفاده می‌کردند و فضایی را برای قرار دادن صفر نگه می‌داشتند. در سرزمین‌های بین‌النهرین (که همانطور که قبلاً دیدیم، از سیستم شصتگانی، یعنی سیستمی با مبنای 60 استفاده می‌کردند) و فرهنگ‌های مایاها و آزتک‌ها (سیستم بیستگانی: سیستمی با مبنای 20)، به مفهومی از صفر نیاز بود تا در عدد نویسی خودشان از آن استفاده کنند. بنابراین اگرچه اذعان می‌شد که باید راهی برای رسیدگی به صفر وجود داشته باشد، اما در این موارد، صفر به طور کامل به عنوان یک عدد مورد توجه قرار نمی‌گرفت.

...........................................

فصل 9

پژواک‌هایی از بغداد

همزمان با گسترش جنگ‌ها و بی‌ثباتی در یونان و جزایرِ سراسر مدیترانه، در جاهای دیگر جهان فرهنگ‌های جدیدی در حال ظهور بودند و قدم در جای یونان می‌گذاشتند. از قرن هشتم تا چهاردهم میلادی، یعنی در دوران طلایی اسلام، بغداد به مرکزِ آموزش در جهان تبدیل شده بود. در اواخر قرن هشتم میلادی، بیت‌الحکمه توسط خلیفه هارون‌الرشید ساخته شد. در آنجا صدها هزار کتاب و اشیاء بسیار مهمِ قدیمی قرار گرفته بود. دانشمندان از گوشه و کنار امپراتوری برای تبادل ایده‌ها، گفتگو با یکدیگر، ترجمه کتاب‌های قدیمی (که بسیاری از آنها مبانی تفکر غرب را زنده نگه می‌داشت) و نوشتن کتاب‌های جدید به آنجا می‌آمدند. در این مکان، ریاضیدانان شروع به ایجاد برنامه‌ای برای جمع‌آوری دانش ریاضی از سراسر جهان، ترجمه و به‌روزرسانی آن، همراه با اختراعات خود کردند.

محمد ابن موسی خوارزمی

در اینجا بود که برای اولین بار سر و کله لغت جبر (Algebra) پیدا شد. این لغت از عنوان کتابی نوشته محمد ابن موسی خوارزمی (حدود 780-850) گرفته شده است.

...........................................

فصل 12

زیبایی در نگاه ریاضیدان است

آیا تا به حال به یک نقاشی مربوط به دوران رنسانس نگاه کرده‌اید، و این حس به شما دست داده که دارید از یک پنجره مستقیماً به قرن پانزدهم نگاه می‌کنید؟ از این جهت، ما باید قدردان ریاضیات باشیم. از زمان افولِ یونانیانِ باستان، نقاشی‌ها شکلی مسطح داشتند و اندازه‌ اشیاء و موقعیت‌ آنها غیرطبیعی به نظر می‌رسیدند. همه اینها در قرن‌های چهاردهم و پانزدهم میلادی با توسعه پرسپکتیو خطی تغییر کرد. پرسپکتیو (perspective) یک تکنیک ریاضی است که یک تصور خیالی از فضای سه‌بعدی را بر روی یک سطح دوبعدی ارائه می‌دهد. هندسه نسبتاً ساده پرسپکتیو چنان شگفتی در هنر ایجاد کرد که هنوز هم ما را به اندازه کسانی که برای اولین بار آن را دیدند، مجذوب خود می‌کند.

سیستم پرسپکتیو براساس چند اصل بنا شده است. این اصول نسبتاً ساده هستند، اما برای اینکه در آنها مهارت زیادی کسب کنید، به ماه‌ها یا حتی سال‌ها تمرین نیاز دارید. تصور کنید که در حال نقاشی یک منظره هستید. فرض اساسی این است که در فضای سه‌بعدی که در آن زندگی می‌کنیم، یک ساختارِ هندسی زیربنایی وجود دارد و ما می‌توانیم بخش‌هایی از آن فضا را بررسی کنیم. سپس در این میان، قابِ بوم شما قرار دارد، که همان خطوط عمودی و محدوده‌های افقی فضایی هستند که به آن نگاه می‌کنید. در این فضا چند شیء وجود دارد. در این مرحله، تصور اینکه از بالا به آنها نگاه می‌کنید و مشخص کردن محل قرارگیری اشیاء می‌تواند مفید باشد. به سه‌پایه خود برگردید. تصور کنید که یک صفحه خاصی در مقابل شما قرار دارد که بین شما و صحنه‌ای که می‌خواهید آن را نقاشی کنید قرار گرفته است. این صفحه (یا بوم) جایی خواهد بود که در نهایت تصویر شما ظاهر می‌شود.

...........................................

فصل 13

جدال بر سر حل معادلات درجه سوم

درست پس از آغاز قرن شانزدهم، ریاضیدانی اهل بولونیا، به نام شیپیونه فرو (Scipione Ferro) (1465-1526)، که معلم حساب و هندسه بود، به ملاقات لوکا پاچیولی آمد. او می‌خواست در مورد روشی که برای حل معادلات درجه سوم (معادلاتی که بالاترین توانِ کمیتِ مجهول 3 است) پیدا کرده بود، گفتگو کند. قرن‌ها بود که مردم می‌دانستند چگونه معادلات خطی و درجه دوم را حل کنند، اما هیچ کس نمی‌توانست معادلات درجه سوم را حل کند. در واقع پاچیولی در پایان کتاب خودش گفته بود که یافتن یک فرمول یا الگوریتم کلی برای معادلات درجه سوم غیرممکن است.

این دو مرد درباره کشف فِرو با هم صحبت کردند. او به نحوی راه حلی برای معادلاتی به شکل x³+cx=d ارائه داده بود، که در آن هم c و هم d اعدادی مثبت هستند. این یک معادله درجه سوم کامل نبود (که بصورت ax³+bx²+cx=d است)، اما همچنان نسبت به آنچه مردم در آن زمان می‌دانستند پیشرفت بزرگی محسوب می‌شد. با وجود این دست‌آورد خارق‌العاده، بنا به دلایلی فِرو نمی‌خواست راه‌حل او تا پیش از مرگش افشا شود. ولی او در بستر مرگش، به موقع این راز را برای شاگردش، آنتونیو ماریا دل فیوره (Antonio Maria del Fiore)، فاش کرد.

...........................................

فصل 17

قبل از اختراع اینترنت، ما مِرسن را داشتیم

مارین مرسن (Marin Mersenne) (1588-1648) یک کشیش کاتولیک از فرقه مینی‌م (Minim) بود. همانطور که از نام این فرقه پیداست، پیروان این فرقه با حداقل‌ها و کمترین چیز‌ها، روزگار می‌گذراندند. شیوه زندگی آنها با پرهیز و اهمیت به فروتنی مشخص می‌شد.

مارین مرسن

بنابراین خنده‌دار است که مردی که در زندگی به کمترین چیزها مقید بود، سیستمی را ابداع کرد که بزرگترین اعداد اول شناخته شده را به ما می‌دهد. بزرگترین عدد اول شناخته شده فعلی که در اکتبر 2024 کشف شد، 2^136,279,841-1 است. تعداد ارقام این عدد 41,024,320 است. چقدر طول می‌کشد تا ارقام چنین عددی را بشمارید؟ جرمی هارپر از ایالات متحده در سال 2007 آزمایشی را برای یک موسسه خیریه انجام داد و با صدای بلند از 1 تا یک میلیون شمرد. اینکار برای او 89 روز طول کشید و هر روز 16 ساعت را صرف شمارش کرد. اگر این عدد را در تقریباً بیست و پنج ضرب کنید، حداقل شش سال طول می‌کشد تا به تعداد ارقام بزرگترین عدد اول شناخته شده فعلی برسید (گفتن همه آن اعداد بزرگ با صدای بلند زمان بسیار بیشتری می‌برد). فکر نمی‌کنم کسی داوطلب شود که این را آزمایش کند، اما چه کسی می‌داند!

...........................................

فصل 19

درهای بسته و ذهن‌های باز

بیشتر روال‌های ریاضی، در هر کجا که ابداع شده باشند، به نوعی و تا حدی در ارتباط یا در تضاد با روالِ دیگر فرهنگ‌ها ساخته شده‌اند. ما قبلاً وقتی برخی از ریاضیدانان با همکاران خودشان در کشورهای دیگر مکاتبه، و حتی با آنها ملاقات می‌کردند تا در مورد ایده‌های خود بحث و گفتگو کنند، چنین مواردی را دیده‌ایم. با گذشت زمان این نوع همکاری‌های فرامرزی افزایش یافت، و بسیاری از شیوه‌های ریاضیاتِ امروز را مشخص کرد.

اما در یک دوره خاص‌، و در یک کشور خاص، تماس‌های بین‌المللی اکیداً ممنوع بود. پس از یک جنگ داخلی صد ساله، مرزهای ژاپن کاملاً بسته شد و این کشور وارد دوره‌ای از انزوا شد که بعدها ساکوکو (Sakoku) (1603-1868) نامیده شد، به این معنی که تمام ارتباطات خارجی (از جمله هرگونه ارتباط علمی، که شامل ریاضیات هم بود) قطع شد. برای اکثر مردم ژاپن، ریاضیات و هر چیز دیگری که در خارج از ژاپن انجام می‌شد، غیرقابل دسترس شد. ولی در پشت این درهای بسته، ریاضیاتِ جدید و بسیار متمایز و زیبایی پرورش یافت، ایده‌هایی که این ریاضیات از آن سرچشمه گرفته بود با اکثر ایده‌هایی که توسط سایر ریاضیدانانِ جهان دنبال می‌شد، متفاوت بود. حتی برای سنتِ ریاضیات ژاپنی این دوره نام مشخصی وجود دارد: ما آن را واسان (和算) (یا ریاضیات ژاپنی) می‌نامیم، که از لغات ژاپنی وا (به معنی ژاپنی) و سان (به معنی محاسبه) گرفته شده.

...........................................

فصل 22

ردپاهای هندسه مدرن

نقطه‌ای را در فضا تصور کنید. فضا همگن (homogenous) است، یعنی هیچ تفاوت کوچکی در اینجا یا آنجا وجود ندارد، و کلاً در همه جا یکسان است. آن نقطه نیز نه طول دارد و نه عرض و نه پهنا، فقط یک نقطه کوچک است. حالا تصور کنید که این نقطه به آرامی شروع به حرکت ‌کند و در حین حرکت، ردی از خود به جا بگذارد. این نقطه در یک جهت مستقیم حرکت می‌کند، و همانطور که حرکت می‌کند، رد آن یک خط مستقیم خواهد بود. حالا تصور کنید که این خط مستقیم، یعنی همان رد نقطه، خودش ثابت باشد. تصور کنید که یک خط مستقیم دیگر در جهت عمود بر آن از روی این خط عبور کند و سپس آن خط جدید شروع به حرکت از روی خط اول ما ‌کند و آن نیز ردی از خود به جا می‌گذارد. این بار، رد این خط به یک صفحه مسطح تبدیل می‌شود.

این تصور که همه چیز در فضا توسط حرکت عناصر هندسی، و ردپایی که آنها از خود به جا می‌گذارند توصیف می‌شود، اساس تکنیکی بود که توسط ریاضیدان فرانسوی، گاسپار مونژ (1746-1818) اختراع شد. او آن را هندسه ترسیمی یا هندسه توصیفی (descriptive geometry) نامید.

گاسپار مونژ

او این نوع توصیف را کامل کرد تا بگوید که کُلِ فضا توسط چنین حرکاتی ایجاد می‌شود و این به روشِ فوق‌العاده محبوبی برای آموزش هندسه در کشورهای سراسر جهان (مخصوصاً تمام سرزمین‌هایی که فرانسه در قرن نوزدهم در آنها نفوذ داشت) تبدیل شد.

...........................................

فصل 24

ریاضیدانانِ عاشق‌پیشه

از زمانی که کاردانو و تارتالیا معادلات درجه سوم را حل کردند (فصل 13)، ریاضیدانان همیشه به امکان حل معادلات با توان‌های بالاتر (بزرگتر از چهار) می‌اندیشیدند. هیچ‌کس نتوانسته بود به روشی مشابه کاردانو و تارتالیا، فرمولی برای حل معادلات درجه پنج و بالاتر ارائه دهد. با توجه به اهمیت این مسئله، ممکن است شما تصور کنید بالاخره یک فرد بسیار خبره این فرمول را کشف کرد، اما در واقع این معما توسط دو ریاضیدان بسیار جوان و بی‌تجربه حل شد.

آنها در عصر رمانتیسم، یعنی زمانی که در سراسرِ جهانِ غرب برخی تغییرات گسترده در حال وقوع بود، زندگی می‌کردند. مردم علیه رژیم‌های خودکامه قدیمی شورش کردند (مانند انقلاب فرانسه)؛ مستعمره‌ها علیه کسانی که آنها را برپا کرده بودند قیام کردند (مانند جنگ استقلال آمریکا). این دوره همچنین عصر بزرگ داستان‌هایی بود که قهرمان‌نان عاشق‌پیشه را به تصویر می‌کشید، شخصیت‌های جوان و تنهایی که هنجارهای مرسوم را رد می‌کنند و به نوبه خود توسط جامعه کلاً طرد می‌شوند. داستان دو ریاضیدان جوان ما نیز به طرز عجیبی دقیقاً چنین بود.

اولین بازیگر ما یک ریاضیدان نروژی بسیار فقیر به نام نیلز هنریک آبل (Niels Henrik Abel) (1802-1829) بود که فقط بیست و هفت سال زندگی کرد.

نیلز هنریک آبل

آبل به یافتن نوعی قاعده برای حل معادلات درجات بالاتر علاقه‌مند بود. درست یک تابستان قبل از مرگش، او در حالی که با نامزدش به تعطیلات رفته بود، یادداشت کوتاهی نوشت.

...........................................

فصل 28

آشکار کردن ابعاد بالا

آیا تا به حال احساس کرده‌اید که در این دنیا گیر افتاده‌اید و آرزو می‌کنید که فقط برای یک ماجراجویی کوچک می‌توانستید برای مدتی به ابعاد ناشناخته سفر کنید؟ بسیاری از داستانهای علمی تخیلی به این موضوع می‌پردازند (مثلاً سفر در زمان یا بازدید از جهان‌های موازی). شاید برخی از ایده‌های ریاضی که قبلاً با آنها مواجه شده‌ایم، باعث شده‌اند که دنیای سه‌بعدی ما با وجود فضای همگن آن، به اصطلاح کمی سطحی به نظر برسد.

برای داشتن نوعی تجربه از ابعاد مختلف، لازم نیست به داستان‌های تخیلی تکیه کنیم. ریاضیات نیز می‌تواند این را به ما ارائه دهد. در واقع، تفکر در مورد ابعاد بالاتر چیزی است که ریاضیدانان قرن‌ها با آن دست و پنجه نرم کرده‌اند. بیایید در این فصل با سفر در زمان، به سراغ برخی از ریاضیدانان پیشین برویم. در قرن هفدهم ریاضیدان انگلیسی، جان والیس (John Wallis) (1616-1703)، می‌گفت حتی تصور بُعدی که جزء یکی از سه بُعد معمول (طول، عرض، و ضخامت) نباشد، یک «خیال‌پردازی» است و یک شیء چهار بعدی در واقع «هیولایی در طبیعت خواهد بود که احتمال وجود آن بسیار کم است».

جان والیس

در واقع، برای قرن‌ها دیدگاه رایج در ریاضیات همین بود. سپس، درست در آغاز انقلاب فرانسه، ژان دالامبر (Jean d’Alembert) (1717-1783) و به طور کامل‌تر، ژوزف-لویی لاگرانژ (Joseph-Louis Lagrange) (1736-1813) این ایده را مطرح کردند که زمان را می‌توان به عنوان بعد چهارم در نظر گرفت.

...........................................

فصل 31

فرانک رمزی و دوستان

به مهمانی‌های خوبی که تا به حال رفته‌اید فکر کنید. بدون شک در آنها دوستان زیادی حضور داشته‌اند، و شاید در برخی از آنها چند غریبه هم حضور داشته‌اند که با آنها گفتگوهای جالبی داشته‌اید. اگر شما می‌خواستید یک مهمانی را ترتیب دهید که شامل ترکیبِ کاملی از دوستان و غریبه‌ها باشد (مثلاً جایی که حداقل سه نفر یکدیگر را بشناسند) آیا باید تعداد زیادی مهمان حضور داشته باشید؟ نه لزوماً. یک گروه مختلط که تنها شامل شش نفر هستند، به طور باورنکردنی آنقدر بزرگ هست که در آن سه نفر باشند که همگی یا آشنای متقابل باشند یا غریبه متقابل.

این مثال، یا بهتر بگوییم، ریاضیات پشت آن، توسط فرانک رمزی (Frank Ramsey) (1903-1930)، فیلسوف، ریاضیدان و اقتصاددان بریتانیایی، که بسیار نوآور بود، توسعه داده شد. این مثال، یک نظریه ریاضی کاملاً جدید را به وجود آورد که اکنون نظریه رمزی نامیده می‌شود، این شاخه‌ کاملی از ریاضیات است که از آن زمان تاکنون در حال توسعه و تأثیرگذاری بوده است.

فرانک رمزی

این موضوع از دهه 1920 آغاز شد، یعنی همان زمانی که رمزی ایده‌های خود در مورد تصمیم‌گیری را با استفاده از منطق در کتاب «درباره یک مسئله منطق صوری» (1930) منتشر کرد.

...........................................

فصل 34

بازی‌هایی که مردم می‌کنند

دو عضو یک باند تبهکار جرمی را مرتکب می‌شوند. آنها بعداً توسط پلیس دستگیر و در سلول‌های جداگانه نگهداری می‌شوند. پلیس می‌داند که آنها این کار را انجام داده‌اند، اما شواهد کافی برای پیگرد قانونی کاملِ آنها ندارد، بنابراین اگر نتواند اطلاعات بیشتری از دستگیرشدگان بگیرد، آنها به اتهام سبک‌تری به یک سال زندان محکوم می‌شوند. اما پلیس به هر زندانی یک معامله پیشنهاد می‌دهد و به آنها می‌گوید اگر علیه شخص دیگر شهادت دهند، آزاد خواهند شد، ولی شخص دیگر سه سال زندان خواهد گرفت. اما یک نکته وجود دارد: اگر هر دو علیه یکدیگر شهادت دهند، هر دو به 2 سال زندان محکوم می‌شوند. ما می‌توانیم ماتریسی شبیه این رسم کنیم تا همه احتمالات را ببینیم.

ولی زندانیان فرصت زیادی برای فکر کردن به این موضوع ندارند و هیچ راهی نیز برای فهمیدن اینکه طرف مقابل چه خواهد کرد، وجود ندارد. اما آنها می‌دانند که به شریک‌جرم آنها هم همین پیشنهاد شده است. در این باند جنایتکار هیچ وفاداری وجود ندارد (تمام زندانیان فقط به فکر خودشان هستند). آنها در چنین موقعیتی چه می‌کنند؟ و به نظر شما بهترین استراتژی چیست؟

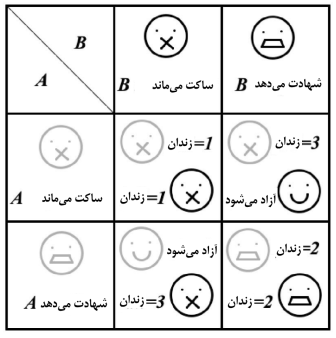
این یک بازی معروف است که به عنوان دوراهی زندانی (prisoner’s dilemma) شناخته می‌شود.

...........................................

فصل 37

عصای جادویی مریم

در سال 1356 شمسی دختری در تهران، پایتخت ایران، به دنیا آمد. او در بحبوحه جنگ ایران و عراق بزرگ شد و دوران سختی را سپری ‌کرد. او دختری باهوش بود و رویای این را داشت که نویسنده شود و درباره دخترانی که به دور دنیا سفر می‌کردند و به دستاوردهای بزرگی رسیده بودند داستان می‌نوشت. او نمی‌دانست که به زودی خودش هم به یکی از این زنان تبدیل خواهد شد و ریاضیات باعث خواهد شد او درگیر ماجراجویی بی‌نظیری در سراسر جهان شود.

مریم میرزاخانی (1396-1356) در یک مدرسه راهنمایی، و سپس در دبیرستان مخصوصِ دخترانِ تیزهوش تحصیل کرد. این مدرسه، یکی از مدارس متعددی بود که توسط دولت‌ برای دانش‌آموزان «بااستعداد و استثنایی» تأسیس شده بود. هنگامی که مریم برای مسائلی که پیش روی او قرار داشت، بیش از یک راه حل ارائه می‌داد (و این تقریباً برای او به یک عادت تبدیل شده بود) استعداد فوق‌العاده او کم‌کم خودش را نشان داد. برای او یک راه حل کافی نبود. او تا حد امکان روش‌های مختلفی را برای حل یک مسئله امتحان می‌کرد و سپس آنها را به دوستان و معلمانش نشان می‌داد. اگرچه واضح بود که او ذاتاً بااستعداد است، اما تمام کسانی که در آن زمان او را می‌شناخت، می‌گفت که او بسیار سخت کوش نیز هست. او همیشه به تمرین ریاضیات می‌پرداخت و از انجام آنها لذت می‌برد. گاهی اوقات به خودش استراحت می‌داد و یک روز کامل کتاب‌های دیگری می‌خواند، و سپس دوباره به ریاضیات بازمی‌گشت.

مریم میرزاخانی (راست) به همراه رویا بهشتی (چپ) 1379، دماغه کاد، ایلات متحده

روزی او و بهترین دوستش رویا بهشتی (که او هم بعدها ریاضیدان شد) به‌طور اتفاقی در دبیرستان به نسخه‌ای از شش مسئله برخوردند که برای المپیاد بین‌المللی ریاضی تنظیم شده بود. ایده یک مسابقه بین‌المللی که در آن جوانان در ریاضیات به رقابت بپردازند، به دهه 1950 میلادی بازمی‌گشت.

...........................................

فصل 38

الگوهای موفقیتِ ریاضی

عکس معروفی از یک پسر بچه ده ساله هست که در سال 1985 کنار پاول اردوشِ کبیر (فصل 31) نشسته. هر دو در حالی که به یک نوشته ریاضی نگاه می‌کنند، چانه‌هایشان را می‌خارانند. اردوش واقعاً با خیلی‌ها دوست بود، اما این پرکارترین ریاضیدانِ زمان، وقت خودش را فقط برای توضیح یک مطلب ریاضی به یک کودک تلف نمی‌کرد. آنها داشتند به طور جدی در مورد یک مسئله ریاضی با هم گفتگو می‌کردند.

ترنس تائو 10 ساله در کنار پاول اردوش 73 ساله (1985).

آن پسر ترنس تائو (Terence Tao) (متولد 1975) بود، که امروزه یکی از مطرح‌ترین ریاضیدانان جهان است. او جوانترین شرکت کننده در المپیاد بین‌المللی ریاضی بود که در سن ده سالگی در مسابقات 1986 شرکت کرد و مدال برنز گرفت؛ سال بعد مدال نقره و سال بعد، در سن سیزده سالگی مدال طلا را از آن خود کرد. او هنوز هم رکورددار جوانترین برنده هر سه مدال در تاریخ المپیاد است. او تحصیلات کارشناسی خود را در رشته ریاضیات در شانزده سالگی به پایان رساند، در بیست و یک سالگی دکترای خود را دریافت کرد و در بیست و چهار سالگی جوانترین استاد تمامِ ریاضیات (در دانشگاه کالیفرنیا، لس آنجلس) شد. ممکن است شما پیش خود فکر کنید ”با وجود چنین اشخاصی، بهتر است سراغ ریاضیات نروم“. اما بعداً در پایان همین فصل توصیه‌های مفید تائو در مورد ریاضیات را خواهیم شنید.

...........................................

فصل 40

رویای داشتن ریاضیاتی جدید

ما در این کتاب تاریخچه ریاضیات، مباحث بسیار زیادی را پوشش داده‌ایم. از جداول و فهرست‌ها، کسرها، و اثبات‌ها عبور کردیم تا ببینیم چگونه ریاضی‌دانان با کسبِ مداوم یک زبان مدرن‌ترِ ریاضی، روش‌ها و تکنیک‌هایی را برای توسعه‌ ایده‌های پیچیده‌تر توسعه داده‌اند، و گویی پایه‌های یک ساختمان در حال ساخت را بنا می‌کنند، آنها طبقه به طبقه پیش رفته‌اند تا اینکه حالا این ساختمان بلند آسمان بالای سرمان را می‌شکافد و ما را به دنیایی با ابعاد دیگر می‌برد.

ریاضیات علمِ الگوهاست، روشی برای یافتن قوانینِ مختصر، کلی، و انتزاعی که زیربنای تمام ساختارهای دیگر را تشکیل می‌دهند و آنها را توصیف می‌کنند، و این چیزی است که این علم را به رشته‌ای مستقل تبدیل می‌کنند. ریاضیات همچنین یک هنر است که از خلاقیت و تراوش تخیلِ ابداع‌کننده‌گان آن بهره می‌برد، و برای عشقِ محض به موضوع ساخته شده است. گاهی اوقات ما فوراً کاربردِ ایده‌های ریاضی را می‌بینیم، اما گاهی اوقات نه، حداقل نه خیلی فوری. ایده‌های ریاضی همیشه کارکردِ مفیدشان را نشان نمی‌دهند . ریاضیات همچنین بیانگر زیبایی عمیق و دقیقی است، و اگر از هر ریاضیدانِ محقق بپرسید که چرا روی آن کار می‌کند، بر زیبایی آن تاکید دارد.

تاریخ ریاضیات پیشینه منحصر به فردی از جهان را به ما ارائه می‌دهد. از غارنشینان ماقبل تاریخ که استخوان یک بابون را حکاکی می‌کردند گرفته، تا چیدمان کره‌ها در بُعد بیست و چهارم، انسان همیشه نیاز داشته تا به هر شکلی با استفاده از زبان ریاضی که در اختیار دارد، الگوها را درک و ثبت کند. این دانش‌های متمایز بعداً به دیگران منتقل شده‌اند. زبانی که این دانش با آن نوشته شده به طرز چشمگیری در طول قرن‌ها پیشرفت کرده است، اما اصول و ایده‌های اساسی که آنها بر آن تأکید دارند، به طور کلی مشابه هستند. شما باید الگویی را تشخیص دهید، آن را به موجزترین، دقیق‌ترین، و انتزاعی‌ترین شکل ثبت کنید و آن را در اختیار دیگران قرار دهید تا در مورد آن فکر کنند.

...........................................

[1] - ایندیانا جونز یک شخصیت خیالی است که به عنوان باستان‌شناس و ماجراجوی مشهور در مجموعه فیلم‌های سینمایی «Indiana Jones» ظاهر شده بود. نقش او توسط هریسون فورد ایفا شد و به یکی از نمادهای فرهنگ عامه بدل شد (مترجم).

[2] - این سنگ اکنون در موزه بریتانیا است.

Like: ,

ترجمه‌های کامران بزرگزاد

show_banner(0);

از زیرخاک درآوردن دانش

اسرار فیثاغورثیان

پرفروش‌ترین کتابِ ریاضی تمام دوران

پس اثبات‌ کجاست؟

طلوع نظریه اعداد

جدال بر سر حل معادلات درجه سوم

قبل از اختراع اینترنت، ما مِرسن را داشتیم

درهای بسته و ذهن‌های باز

ریاضیدانانِ عاشق‌پیشه

آشکار کردن ابعاد بالا

فرانک رمزی و دوستان

عصای جادویی مریم

رویای داشتن ریاضیاتی جدید