بر اساس تقسیم بندی که انجمن ریاضیات آمریکا انجام داده، از میان 60 شاخهِ مختلفِ ریاضیاتِ قرن 21، حدود 13 شاخه به جبر تعلق دارد (یعنی حدود 22 درصد). بنابراین، به جرات می‌توان ادعا کرد که جبر گسترده‌ترین و پرکاربردترین حوزه در میان شاخه‌های مختلف ریاضیات است. همچنین، جبر پس از حساب و هندسه قدیمی‌ترین شاخه ریاضیات است.

با توجه به ریشه عربی لغت ”جبر“، و اینکه اولین بار خوارزمی، و بعدها خیام نیشابوری، از این لغت در عنوان کتاب‌هایشان استفاده کردند، خیلی‌ها تصور می‌کنند که زایش این رشته در ایران، و کلاً در شرق بوده. ولی این بستگی دارد که چه چیزی را جبر بدانیم.

آنچه در زمان خوارزمی و خیام بعنوان جبر مطرح بود، پیوند تنگاتنگ و جدایی‌ناپذیری با معادلات داشت، و معمولاً همراه با مُقابله از آن یاد می‌شد. جبر و مقابله ابزارهایی برای حل معادلات مختلف، از درجه 1 تا درجه 3، و همینطور معادلات چند مجهوله بودند. ولی امروزه جبری که خوارزمی و خیام به آن روش کار می‌کردند، نه فقط با جبر مدرن کوچکترین شباهتی ندارد، بلکه حتی با آنچه ما در دبیرستان بعنوان جبر یاد می‌گیریم هم فاصله دارد. آنچه از حدود چهارصد سال قبل تاکنون در جبر مرسوم بوده استفاده از حروف مختلف الفبای لاتین و یونانی، مثل a، b، x، α، β، π، و غیره برای نشان دادن کمیت‌های مختلف است. در زمان خیام و خوارزمی نه تنها از چنین علامت‌هایی، بلکه حتی از نمونه‌های عربی آنها مثل الف، ب، ج، ... و غیره هم استفاده نمی‌شد. آنها برای بیان همه کمیت‌ها، چه معلوم و چه مجهول، از اسامی خاصی، مثل شیء، ریشه، مکعب، مربع ... استفاده می‌کردند. آنها حتی علامت‌هایی مثل +، -،× ، ÷ را نداشتند تا برای نشان دادن عملیاتِ حسابی از آنها استفاده کنند. در آن زمان همه چیز بصورت لفظی و با استفاده از جملات طولانی و ملال‌آور بیان می‌شد.

جبر امروزی، یعنی استفاده از علائم بجای کمیت‌های مختلف، با کارهای دیافانتوس شروع شد. ولی از قرن چهارم میلادی به بعد، بعلت ورود اروپا به قرون تاریک، به مدت 1400 سال کارهای دیافانتوس فراموش شد، و تنها در دوران رنسانس بود که اروپاییان قدر کارهای او را دانستند، و از آن زمان به بعد یک سیستم نمادگذاری جبری توسعه داده شد، و تقریباً از اوایل قرن 17 میلادی، به همان صورتی درآمد که ما امروز در جبر دبیرستانی با آن آشنا هستیم.

ولی این تنها شروع کار بود. از حدود دویست سال قبل به این سو، یعنی از اویل قرن نوزدهم، جبر متحول شد و اشکال جدیدی پیدا کرد. مهمترین تغییری که در این حوزه پدید آمد این بود که دیگر صرفاً برای نشان دادن اعداد از علائم استفاده نمی‌شد، بلکه باظهور اشیاء دیگر ریاضی، مثل ماتریس‌ها، گروه‌ها، گزاره‌های منطقی، یا جایگشت‌ها، از این علائم برای نمایش آنها نیز استفاده می‌شد.

چیز مهمی که از نیمه دوم قرن نوزدهم پدید آمد، پیدایش اشیاء جدید و بدنبال آن جبرهای مختلف بود: جبر کواترنیون‌ها، جبر ماتریسی، جبر بول، گروه‌ها، حلقه‌ها، ... و غیره. این روند با ظهور اشیاء جدید ریاضی همچنان ادامه پیدا کرده. ولی آنچه در این میان اهمیت دارد، و جبر را از بقیه حوزه‌های ریاضیات متمایز می‌کند، قدرت آن بعنوان یک ابزار وحدت بخش است. حالا جبر در بسیاری از حوزه‌های سنتی ریاضیات از قبیل نظریه اعداد، هندسه، آنالیز، و حتی حوزه‌های جدیدتر آن مانند توپولوژی، رسوخ پیدا کرده و موجب غنای آنها شده، و به عاملی برای پیوند آنها بدل شده. حالا ما رشته‌های جدیدی داریم که هر چند قبلاً جزیی از ریاضیات سنتی بودند ولی ترکیب آنها با جبر باعث شده به شدت به جبر وابسته باشند: نظریه جبری اعداد، هندسه جبری، توپولوژی جبری، ... و غیره.

آنچه از اواخر قرن نوزدهم در این حوزه انجام شد، حالا از آن تحت نام جبر نوین، یا جبرِ مجرد نام برده می‌شود، و شباهت اندکی با جبر دبیرستانی، یا جبر سنتی 400 سال قبل دارد. با پیشرفت جبر و ورود آن به قلمروهای جدید، باز هم از این شباهت کاسته می‌شود. این روند 170 ساله را می‌توان در یک کلام خلاصه کرد و آن انتزاعی‌تر شدن جبر است.

واجب می‌دانم روی لغت ”انتزاعی“ تمرکز کنم. دلیل آن هم این است که گرچه یادگیری جبر مجرد مانند هر رشته دیگری نیازمند تلاش و تمرین فروان است، ولی اگر معنی لغت انتزاعی برای شما روشن باشد، می‌توان ادعا کرد که جانِ کلامِ جبرِ نوین را دریافته‌اید. در خیلی از کتاب‌های فلسفه، ریاضی، و حتی علوم‌ کامپیوتری، از لغت انتزعی (یا معادل آن، ”تجریدی“) زیاد استفاده می‌شود. ولی اگر از دانشجویان مبتدی این رشته‌ها، خصوصاً رشته‌های ریاضی و مهندسی سئوال شود که معنی لغت انتزاعی، یا تجرید چیست، یا مثلاً مراد از لغت ”مجرد“ در اصطلاح ”جبرِ مجرد“ چیست، با اینکه زیاد از آن استفاده می‌کنند، درک درستی از آن ندارند. ولی قبل از اینکه معنی این لغات را توضیح دهم، می‌خواهم تاکید کنم که در این کتاب هم از لغت ”انتزاع“ و هم از لغت ”تجرید“ و مشتقات آنها استفاده شده، و معنی آنها هم یکی است. کاربرد هر کدام از این لغات به زمینه جمله بستگی داشته. مثلاً هم می‌توان از اصطلاح ”جبرِ انتزاعی“، و هم از ”جبرِ مجرد“ استفاده کرد، ولی دومی مرسوم‌تر است.

”انتزاعی“ یک لغت عربی است که در خیلی از زبان‌های اروپایی معادل لغت ”abstract“ است. ما چیزهایی را انتزاعی می‌دانیم که حواسِ ما آنها را حس نکنند، چیزهایی مثل اعداد، تصورات، ... ولی آنچه در اینجا برای ما اهمیت دارد، این واقعیت است که انتزاع درجات مختلفی دارد. یعنی اگر همین معنی ساده را برای ”اشیاء انتزاعی“ در نظر بگیریم (یعنی اشیائی که حواس ما آنها را حس نمی‌کنند)، در میان آنها باز هم اشیائی هستند که گرچه ما آنها را حس نمی‌کنیم (نمی‌بینیم، نمی‌شنویم، نمی‌بوییم، ...) ولی درکی از پیچیدگی آنها داریم، و بر اساس سلسله مراتب فرضی آنها، می‌توانیم بفهمیم که کدامیک ساده‌تر و کدامیک پیچیده‌ترند. معلوم است که ”عدد“ یک مفهوم انتزاعی است، ولی ما عدد داریم تا عدد: اعداد صحیح، اعداد گویا، اعداد گنگ، اعداد جبری، اعداد حقیقی، اعداد مختلط، کواترنیون‌ها، اوکتونیون‌ها ... همه اینها عدد هستند ولی معلوم است که هر کدام از رده‌های قبلی خودشان پیچیده‌ترند. حالا ما اشیاء ریاضی دیگری داریم که یکی از اجزاء تشکیل دهنده آنها می‌تواند عدد (یا چیز دیگری) باشد، بنابراین نسبت به اعداد پیچیده‌ترند: ماتریس‌ها، میدان‌ها، گروه‌ها، حلقه‌ها، ایده‌آل‌ها، چندگوناها ... برای انجام عملیات روی این اشیاء ریاضی، ما به جبرهای متفاوتی نیاز داریم، و هربار این جبرها پیچیده‌تر، یا به عبارتی انتزاعی‌تر می‌شود، به صورتی که آن جبری که پیش از نیمه قرن نوزدهم در جریان بود، و فقط مختصِ کار با اعداد بود، شباهتی به جبرهای مجردِ امروزی ندارد. مثال دیگری که می‌توان برای درجات مختلف انتزاع بیان کرد، و کسانی که با علوم نرم‌افزاری و برنامه‌نویسی آشنا هستند بخوبی آن را درک کرده‌اند، مفهوم ساختار داده‌ها است. این ساختار سلسله مراتبی دارد که می‌تواند از Byte شروع شده به Word، به String، به آرایه‌ها، ... و بعد به کلاس‌ها برسد. این کلاس‌ها می‌توانند هر درجه‌ای از پیچیدگی را داشته باشند. اگر بایت را معادل یک عدد صحیحِ ساده بگیریم، که حداکثر بزرگی آن 256 باشد، یک کلاس می‌تواند آنقدر بزرگ شود که پیچیدگی آن در حد مدل‌سازی یک هواپیما، یک اقتصاد، یا حتی یک موجود زنده شود. چنین کلاس‌هایی دارای چنان سلسله مراتب تو در تو هستند که می‌توانند شامل صدها، هزاران، و میلیون‌ها کلاس دیگر باشند. چیزی که از لحاظ جبری اهمیت دارد این است که ما می‌توانیم هر یک از نمونه‌های (instance) این ساختارهای پیچیده را با یک علامت ساده مثل A و B نشان داده و حتی با علائمی مثل +، یا * عملیاتی را روی آنها انجام دهیم. این مثال ساده‌ای از جبر کامپیوتری و درجات مختلفِ انتزاع (تجرید) بود. البته در ریاضیات جبر، و بخصوص ”یک جبر“ (An algebra)، تعریف متفاوتی دارد که برای جزئیات آن باید فضاهای برداری را مطالعه کنید.

آنچه ما امروز در پیشرفته‌ترین مباحث جبر نوین داریم، نسبت به موارد قبلی حالتی کلی‌تر و انتزاعی‌تر دارند. اینکه این انتزاع چه حدی دارد و تا کجا می‌تواند جلو برود، موضوعی است که بیشتر جنبه فلسفی دارد، و در فصل آخر این کتاب،تحت عنوان ”از حسابِ عام تا جبرِ عام“، به آن پرداخته می‌شود.

جبر در ایران

همانطور که در ابتدای این مقدمه ذکر شد، اگر از جبرِ لفظیِ خوارزمی و خیام صرف‌نظر کنیم، برای چندین قرن نه تنها در ایران، بلکه در کل مشرق زمین، پیشرفتی در این حوزه صورت نگرفت. کارهای این دو ریاضیدانِ پیشرو را هم باید در حوزه حلِ معادلات بررسی کرد (برای جزئیات بیشتر به فصول دوم و سوم این کتاب رجوع کنید). آنها لغت جبر را برای ما بجا گذاشتند، ولی نه آن جبری که از 400 سال قبل به این سو در جریان بوده و ما با آن مأنوس هستیم.

شروع جبرِ سُنتیِ اروپایی در ایران، و آموزش نظام‌مند آن، به حدود 150 سال قبل، و زمانی باز می‌گردد که مدرسه دارالفنون توسط امیرکبیر در تهران تاسیس شد. البته این مختص به جبر نبود، بلکه موارد دیگری از ریاضیات اروپایی، مثل حسابان (که در آن زمان به حساب جامعه و فاضله معروف بود)، را هم دربر می‌گرفت. ولی بازهم تا چندین دهه از جبر نوین خبری نبود.

در آغازِ کارِ دانشگاه تهران و تاسیس گروه‌ ریاضی آن، بیشتر دروس بر مواردی متمرکز بودند که در رشته‌های فنی/مهندسی کاربرد داشتند، موضوعاتی مثل حسابان، هندسه، معادلات دیفرانسیل، ... تخصص استادان پیش کسوت ریاضی ایران، (کسانی مثل دکتر محسن هشترودی، دکتر علینقی وحدتی، دکتر غلامحسین مصاحب، و غیره)، بر روی حوزه‌های سنتی ریاضیات مثل هندسه، آنالیز، و یا نظریه اعداد بود. البته همه این بزرگواران که متولد اواخر دوران قاجار بودند، در دهه‌های 1930 تا 1950 در دانشگاه‌های اروپایی تحصیل کرده بودند و مسلماً با جبر نوین آشنایی داشتند، ولی همانطور که ذکر شد تخصص آنها جبرِ نوین نبود. تنها در دهه 1330 شمسی بود که آموزشِ نظام‌مند جبر نوین (نظریه گروه‌ها، میدان‌ها، حلقه‌ها، ...) در دانشگاه تهران شروع شد.

جبر نوین، یا همان رشته‌ای که خیلی اوقات بعنوان جبرِ مجرد از آن نام برده می‌شود، بر اصولِ‌موضوعه پایه‌گذاری شده که اساس آنها را نظریه مجموعه‌ها تشکیل می‌دهد. نظریه مجموعه‌ها نیز جزئی از مواد درسی بود که ورود آنها به ایران دیر آغاز شد. این موضوع ابتدا در دهه 1320 به دروس ریاضی دانشگاهی وارد شد. ولی نظریه مجموعه‌ها بقدری برای ریاضیات مهم بود که آموزش آن حتماً می‌باید از اوایل دوران متوسطه، و در دبیرستان شروع می‌شد. اینکار با تغییر نظام آموزشی ایران در اوایل دهه 1350 و ایجاد مقطع راهنمایی آغاز گشت. کسی که در آن زمان سهم زیادی در تغییر کتابهای درسی دوره متوسطه ایران داشت، مرحوم دکتر میرزا جلیلی بود، که با تلاش او و همکارانش بسیاری از رئوس جبرِ نوین به دروس متوسطه وارد شد، و حالا حدود 50 سال است که اصول مقدماتی این موضوعات در دبیرستان‌ها آموزش داده می‌شود.

درباره این کتاب

کتاب حاضر سیر تکامل جبر را از زمان دیافانتوس، یعنی قرن دوم میلادی، تا ابتدای قرن بیست و یکم بررسی می‌کند. کتاب هم جنبه‌های تاریخی، و هم جنبه‌های فنی دارد. برای درک اکثر بخش‌های فنی کتاب، داشتن معلوماتی در حد جبرِ دبیرستانِ رشته‌های ریاضی کفایت می‌کند. برای مباحث پیشرفته‌تر هم نویسنده تلاش کرده تا آنجا که امکان دارد با مطرح کردن پیش‌زمینه‌های لازم موضوعات را ساده کند.

درباره نویسنده

جان داربی‌شِر (John Derbyshire) متولد 1945، دانش‌آموخته ریاضی از دانشگاه لندن است. او نویسنده، مفسر سیاسی، روزنامه‌نگار، و برنامه‌نویس کامپیوتر می‌باشد. وی در انگلستان متولد شد و در 30 سالگی تابعیت آمریکا را نیز گرفت.

این دومین کتابی است که من از داربی‌شِر ترجمه می‌کنم. کتاب قبلی دغدغه اعداد اول بود، که به فرضیه ریمان ارتباط داشت. بیشتر کتابهای او به مسائل سیاسی و بین‌المللی مربوطند. خود من هم از طریق یک برنامه سیاسی تلویزیونی با او آشنا شدم، و با جستجویی که درباره او انجام دادم فهمیدم دستی هم در ریاضیات دارد. او همچنین از اواسط دهه 1970 به کار برنامه نویسی کامپیوتر اشتغال داشته. بنابراین با توجه به علائق شخصی خودم، احساس کردم که با نویسنده‌‌ای روبرو هستم که زمینه‌های فکری و کاری متنوعی دارد، و تصمیم گرفتم آثار او را بخوانم. همانطور که متذکر شدم، بیشتر نوشته‌های داربی‌شِر به سیاست و جامعه‌شناسی مربوطند و آثار ریاضی او اندک‌ است، ولی دو کتابی هم که درباره ریاضیات نوشته برجسته و خواندنی هستند. کتاب دغدغه اعداد اول او در سال 2004 برنده جایزهِ کتابِ انجمن ریاضی آمریکا شد.

از لحاظ سیاسی، داربی‌شِر یک محافظه‌‌کارِ ملی‌گرا محسوب می‌شود، ولی نه شبیه کسانی مانند دونالد ترامپ، یا حتی جورج بوش. او گفته بود از بسیاری جهات طرفدار هیلاری کلینتون است. او حتی در اوایل دهه 1970 در فیلم اکشن”راهِ اژدها“ با بازی بروس لی، نقش کوچکی را داشت. او به دلیل علاقه‌ای که به فرهنگ چینی دارد، نهایناً با یک زن چینی تبار ازدواج کرد، که بعداً شهروند آمریکا شد.

پاییز 1401

کامران بزرگزاد

مقدمه مؤلف

1

01/04/1401

تصحیح 1: 26/08/1401

این کتاب درباره تاریخ جبر است و برای خوانندگانِ کنجکاوی نوشته شده که خیلی اهل ریاضی نیستند. از نظر من، نویسنده چنین کتابی باید با این شروع کند که جبر چیست؟ پس من هم با همین شروع می‌کنم.

به تازگی وقتی در فرودگاه بودم، داخل یک کتابفروشی رفتم که تعداد زیادی از کتابهای درسی دبیرستانی و دانشگاهی را در آنجا به نمایش گذاشته بود. دو نمونه از کتاب‌هایی که درباره جبر بودند، چنین عناوینی داشتند: ”جبر 1“، ”جبر 2“، و ”ترکیب جبر 1 و 2“، که در عنوان فرعی آنها ذکر شده بود که پوشش دهنده جبرِ پایه، جبرِ متوسطه، و همچنین جبر دانشگاهی است.

من نگاهی به فهرست عناوین آنها انداختم. از نظر بسیاری از ریاضیدانان حرفه‌ای، خیلی از عناوین این کتابها موضوعات جبری بحساب نمی‌آید. برای مثال، ”توابع“، یا ”دنباله‌ها و سری‌ها“ به حوزه‌ای تعلق دارند که ریاضیدانان به آن آنالیز (analysis) می‌گویند. آن طور که در دبیرستان‌ها و دانشگاه‌های امروز آمریکا مطرح می‌شود، لغت ”جبر“ بطور خلاصه چنین تعریف می‌شود: جبر حوزه‌ای از ریاضیات پیشرفته است که بخشی از حسابان نیست.

ولی در سطوح بالاتر ریاضیات، خود جبر خصوصیات متمایزی دارد که باعث می‌شود رشته خاصی را تشکیل ‌دهد. یکی از معروفترین نقل‌قول‌هایی که توسط ریاضیدان بزرگ آلمانی هرمان ویل (Hermann Weyl) در 1939 نقل شده چنین می‌گوید:

این روزها، فرشته توپولوژی و دیوِ جبرِ مجرد برای بدست آوردن روحِ ریاضیات باهم در جنگ هستند.

شاید خواننده بداند که توپولوژی (topology) شاخه‌ای از هندسه است، که گاهی اوقات بعنوان ”هندسه صفحات-لاستیکی“ از آن نام می‌برند. توپولوژی با خصوصیاتی از اشکال سر و کار دارد که با کشیدن و فشردن آنها تغییر نمی‌کنند، و تنها پاره کردن اشکال می‌تواند خصوصیات آنها را تغییر دهد. (خوانندگانی که با توپولوژی آشنا نیستند می‌توانند برای توضیحات بیشتر به بخش 14.2، و برای آنچه ویل به آن اشاره کرده به بخش 14.6 رجوع کنند.) توپولوژی به ما تفاوتِ میان یک ریسمان صاف و یک ریسمان گره‌خورده، و یا تفاوت میان سطح یک کره و سطح یک تیوپ ماشین را می‌گوید. ولی چرا ویل این تحقیقاتِ بی‌آزار هندسی را در چنین تقابل قوی با جبر قرار داده بود؟

اگر به فهرستی که در بخش 15.1 در مورد مباحث مرتبط با جبر آمده نگاه کنید، چیزهایی نظیر: نظریه میدان کلاس غیر-منشعب (Unramified class field theory)، چندگوناهای ژاکوبی (Jacobean variety)، میدان‌های تابعی، یا کوهومولوژی جبری، آنگاه بسادگی خواهید دید که ما از آنچه قبلاً بعنوان جبر می‌شناختیم، چیزهایی مثلِ معادلات درجه دوم و رسم نمودارها، خیلی دور شده‌ایم. ویژگی مشترکی که در جبر امروز وجود دارد چیست؟ جواب کوتاه این سئوال در نقل قول هرمان وایل پنهان شده: ویژگی مشترکی که در جبر امروز وجود دارد، وجودِ تَجرید یا انتزاع (abstraction) در آن است.

2

البته، کُل ریاضیات جنبه تجریدی (انتزاعی) دارد. اولین تجریدِ ریاضی چندین هزار سال قبل، و هنگامی رخ داد که انسان شروع به کشف اعداد نمود، و مثلاً از مفهوم ”سه-بودن“ به خود عدد سه رسید (یعنی برای رجوع به یک مفهوم ذهنی (انتزاعی) مانند سه، نیازی نبود بگوید سه انگشت، سه گاو، سه ستاره و غیره، خود عدد سه برای اینکار کفایت می‌کرد).

سطح دوم این انتزاع در دهه‌های اول 1600 میلادی، در زمانی اتفاق افتاد که انسان نمادنویسی حرفی را اتخاذ کرد، یعنی استفاده از نمادهای حرفی برای نمایش یک کمیتِ عددی معلوم یا مجهول: به عبارتی داده‌ها (که چیزهای معلوم باشند)، یا مجهولات (چیزهایی که ما به دنبال یافتن آنها هستیم). این همان چیزی است که سر آیزِک نیوتون به آن ”حسابِ عام“ (Universal arithmetic) می‌گفت. انگیزه پیمودن این مسیر طولانی و پرپیچ و خَم که تا آن مرحله صورت گرفته بود، عمدتاً بواسطه تمایل به حلِ معادلات بود، چیزی که در برخی مواقع به آن تعیین کمیت‌های مجهول گفته می‌شود. آنچه ما در ذهن خودمان از لغت ”جبر“ برداشت کرده‌ایم، در طول پیمودن همین مسیر حاصل شده، و من در بخش اول کتاب این مسیر را شرح خواهم داد.

اگر در سال 1800 میلادی از یک شخص تحصیل کرده سئوال می‌شد که جبر چیست، جواب او چیزی شبیه بالا بود (یعنی استفاده از علائم حرفی برای انجام محاسبات و حل معادلات). در آن زمان داشتن تبحر، یا آشنایی مختصر در استفاده از علائم ریاضی، جزیی از آموزش‌های ریاضی در اروپا بود.

ولی در طول قرن نوزدهم میلادی، این علائم خودشان را از قید اعداد جدا کردند. چندین شیء جدیدِ ریاضی کشف شدند، چیزهایی مثل گروه‌ها، ماتریس‌ها، مِنیفُلدها، و بسیاری از اشیاء دیگر. ریاضیات به سطوح بالاتری از تجرید صعود کرد. هنگامی که این نمادگرایی از سوی همه مورد پذیرش قرار می‌گرفت، این روند به جزیی از توسعه طبیعی استفاده از علائم تبدیل می‌شد. بنابراین اگر آن را بعنوان ادامه تاریخ جبر در نظر بگریم، غیر معقول نخواهد بود.

من کتابم را به سه بخش تقسیم کرده‌ام:

بخش 1: که دوران اولیه اتخاذ رویکرد نمادگرایی حرفی را تا پیش از سال 1600 میلادی توضیح می‌دهد.

بخش 2: اولین پیروزی‌های نمادگرایی و آغاز رهایی نمادها از مفاهیم سنتیِ حساب و هندسه، که به کشف اشیاء جدید ریاضی منجر شد.

بخش 3: که دوران جبر نوین را شکل می‌دهد، یعنی قرار دادن اشیاء جدیدِ ریاضی بر پایه یک بنیانِ مستحکمِ منطقی و صعود به سطوح بالاتری از تجرید.

مانند بقیه اکتشافات انسان، توسعه جبر هم نامنظم و اتفاقی بود. به همین دلیل برای من مشکل بود تا در تدوین این کتاب صرفاً به یک رویکرد تاریخی وفادار بمانم، خصوصاً در طول قرن نوزدهم. صرف نظر از اینکه خواننده دید روشنی از کلیه خطوطِ توسعه جبر خواهد گرفت یا نه، امید من این است که این کتاب قابل درک باشد.

3

هدف من این نیست که به خواننده جبرِ پیشرفته را یاد دهم. برای اینکار بسیاری از کتاب‌های درسی خوب وجود دارند، که در طول این کتاب به چند تا از آنها اشاره خواهم کرد. بنابراین، کتاب حاضر یک کتاب درسی نیست. من فقط امیدوارم بتوانم نشان دهم که ایده‌های جبری به چه چیزی شبیه هستند، چگونه ایده‌های جدید بر اساس ایده‌های قبلی توسعه یافته‌اند، و چه کسانی که در اینکار دخیل بوده‌اند، و اینکارها تحت چه شرایطِ تاریخی انجام شده.

ولی بدون ارئه برخی توضیحاتِ حداقلی درباره اینکه این متخصصینِ جبر چه کاری انجام می‌دادند، چنین کاری غیر ممکن بود. بنابراین در این کتاب مقداری ریاضیات نیز آمده است. در جاهایی که حس کردم باید به مباحثی بپردازم که فراتر از ریاضیات دبیرستانی هستند، آنها را بطور خلاصه در بخش‌هایی تحت عنوان ”بخش ریاضی“ گنجانده‌ام. برای درک بهتر مطالب، ممکن است خواننده نیاز داشته باشد تا با این بخش‌های ریاضی آشنا باشد، بنابراین هر یک از آنها پیش از اینکه در روایت تاریخی به آنها اشاره شود، آمده‌اند. در برخی موارد، من در متن اصلی کتاب روی این مفاهیم تکیه بیشتری کرده‌ام. بخش‌های ریاضی به این منظور تدوین شده‌اند تا برای خوانندگانی که قبلاً برخی دوره‌های دانشگاهی را گذرانده‌اند نوعی یادآوری باشند، یا برای خوانندگانی که چیزی درباره این موضوعات نمی‌دانند، یک درک بسیار پایه‌ای را فراهم آورند.

4

خواننده باید توجه داشته باشد که این کتاب بر اساس کتاب‌های دست اولی گردآوری شده که حاصل کار دیگران هستند. هر جا که لازم باشد، من خواننده را به این کتاب‌ها ارجاع خواهم داد. ولی در اینجا سه منبع مهم وجود دارند که من غالباً به آنها رجوع کرده‌ام و لازم است در همین ابتدا به آنها اشاره کنم. اولی فرهنگ بیوگرافی علمی است، که خیلی جاها تحت عنوان DSB[1] از آن یاد می‌شود. این کتاب نه فقط جزئیاتی از زندگی ریاضیدانان را فراهم آورده، بلکه نشانه‌های ارزشمندی بدست می‌دهد که ایده‌های ریاضی از کجا سرچشمه گرفته، و چگونه پراکنده شده‌اند.

دو کتاب دیگری که من شدیداً به آنها تکیه داشته‌ام، کتاب‌های تاریخِ جبر هستند که توسط ریاضیدانان و برای ریاضیدانان نگاشته شده‌اند. یکی از آنها تاریخ جبر نوشته ریاضیدان هلندی وان در واردن (B. L. van der Waerden) و دیگری آغاز و سیر تکامل جبر نوشته ایزابلا باشماکووا (Isabella Bashmakova) است.

5

بنابراین ما در اینجا تاریخ جبر را مرور خواهیم کرد. این داستان از گذشته‌های دور و زمانی آغاز می‌شود که انسان از یک رویکرد خَبری به یک رویکرد پرسشی روی آورد، یعنی بجای اینکه بگوید ”این عدد بعلاوه آن عدد مساوی فلان عدد است“ گفت ”این عدد بعلاوه چه عددی مساوی فلان عدد است؟“ درست در همین زمان بود که x، یا همان کمیت مجهولی که همه ما آن را به جبر وابسته می‌دانیم، وارد فکر انسان شد و باعث شد این نیاز را حس کند که استفاده از علائم برای نمایش مجهولات و اعدادِ مفروض مفید است. هنگامی که این نمادگرایی آغاز شد، به انسان اجازه داد تا در سطوح بالاتری از تجرید به مطالعه معادلات بپردازد. در نتیجه، اشیاء جدید ریاضی بوجود آمدند، و باعث ظهور سطوح بالاتری از تجرید شدند.

در حال حاضر در میان رشته‌های ریاضی، جبر ظریف‌ترین و دشوارترین رشته در میان آنها است، حوزه‌ای که همه اشیاء آن تجریدی هستند، تجریدهایی عمیق و تو در تو از تجریدهای قبلی. بااینحال، نتایجی که از آنها حاصل می‌شود دارای چنان قدرت و زیبایی هستند که فقط برای ریاضیدانان حرفه‌ای قابل درک است. و آنچه شگفت‌انگیزتر و مرموزتر به نظر می‌رسد این است که این اشیاء ذهنیِ ملکوتی، در درون تجریدِ تودرتوی خودشان، حاوی عمیق‌ترین، و بنیادی‌ترین اسرار جهان فیزیکی باشند.

موضوعات ریاضی

اعداد و چند جمله‌ای‌ها

1

در میان روایات تاریخی این کتاب، من داستان را قطع کرده و به موضوعات ریاضی می‌پردازم که برای دنبال کردن داستان لازم است آنها را بدانید، یا آنها را بخاطر آورید.

این اولین بخش ریاضی کتاب است، که به دو مفهوم مهم می‌پردازد که برای دنبال کردن داستان اصلی باید بخوبی آنها را درک کرده باشید. این دو مفهوم، یکی اعداد و دیگری چندجمله‌ای‌ها (polynomial) هستند.

2

مفهومِ امروزی اعداد چیزی شبیه عروسک‌های روسی است. این مفهوم در اواخر قرن 19 شکل گرفت و کم‌کم در دهه‌های 1920 و 1930 در میان ریاضیدانان فراگیر شد. در این مدل پنج عروسک روسی قرار دارند که با حروف توخالی ℕ، ℤ، ℚ، ℝ، و ℂ نامگذاری شده‌اند (شکل 1).

عروسک‌های روسی که هر یک در داخل دیگری قرار می‌گیرند.

درونی‌ترین عروسک، که از همه کوچکتر است و در داخل بقیه جای گرفته، عروسکِ اعداد طبیعی (Natural numbers) است، که آن را با علامت ℕ نشان می‌دهند. اعداد طبیعی همان اعداد شمارشی معمولی 1, 2, 3,… … هستند، و می‌توان آنها را بصورت یک خط نقطه چین نشان داد که از سمت راست تا بی‌نهایت امتداد یافته است:

شکل 1: خانواده اعداد طبیعی یا ℕ.

اعداد طبیعی خیلی مفیدند، ولی چند کمبود مهم دارند. کمبود اصلی آنها این است که همیشه نمی‌توان یک عدد طبیعی را از عدد طبیعی دیگر کم کرد، بصورتی که حاصل آن عدد طبیعی دیگری باشد، یا یک عدد طبیعی را بر عدد طبیعی دیگر تقسیم کرد که حاصل آن عدد طبیعی دیگری باشد. شما می‌توانید 5 را از 7 کم کنید. ولی نمی‌توانید 12 را از 7 کم کنید (البته منظورم این است که می‌توانید اینکار را انجام دهید، ولی حاصل آن یک عدد طبیعی نیست). اصطلاح فنی آن این است که ℕ تحت عمل تفریق بسته نیست. همچنین ℕ تحت تقسیم نیز بسته نیست: شما می‌توانید 12 را بر 4 تقسیم کنید، ولی بدون اینکه از قلمرو ℕ خارج شوید، نمی‌توانید آن را بر 5 تقسیم کنید.

با کشف صفر و اعداد منفی، مشکل تفریق حل شد. در حدود سالها 600 میلادی، صفر توسط ریاضیدانان هندی کشف شد. اعداد منفی نیز ثمره دوران رونسانس اروپا بودند. توسعه دستگاه اعداد طبیعی برای شامل کردن این اعداد جدید، به ایجاد عروسک روسی دوم منجر شد، که عروسک قبلی را در درون خودش داشت. این دستگاه جدید، که اعداد صحیح (integers) نام دارند، را با علامت ℤ نشان می‌دهند که مخفف لغت آلمانی ”Zahl“ به معنی عدد است. اعداد صحیح را می‌توان بصورت یک خط نقطه چین نشان داد که از هر دو طرف چپ و راست تا بی‌نهایت امتداد یافته است:

شکل 2: خانواده اعداد صحیح یا ℤ.

حالا با این دستگاه جدید ما می‌توانیم جمع، تفریق، و ضرب را انجام دهیم، هرچند برای ضرب این اعداد، ما باید قواعد علامت‌ها را در نظر بگیریم:

مثبت در مثبت می‌شود مثبت.

مثبت در منفی می‌شود منفی.

منفی در مثبت می‌شود منفی.

منفی در منفی می‌شود مثبت.

بطور خلاصه، حاصل ضرب علامت‌های مشابه در هم، مثبت، و حاصل ضرب علامت‌های نامشابه در هم، منفی است. قاعده ضرب علامت‌ها درمورد تقسیم نیز صدق می‌کند. بنابراین حاصل تقسیم -12 بر -3 می‌شود 4.

ولی معمولاً تقسیم در ℤ امکانپذیر نیست. زیرا ℤ تحت تقسیم بسته نمی‌باشد. برای بدست آوردن دستگاه اعدادی که تحت تقسیم بسته باشد، در اینجا نیز باید ℤ را گسترش دهیم، تا دستگاهِ حاصله شامل کسرهای مثبت و منفی نیز باشد. حاصل اینکار عروسک روسی سوم است، که حاوی دو عروسک کوچکتر از خودش، یعنی اعداد طبیعی و اعداد صحیح، می‌باشد. این عروسک جدید اعداد گویا نامیده می‌شود، و آن را با ℚ نشان می‌دهند (در اینجا Q مخفف Quotient، به معنای خارج قسمت تقسیم است).

اعداد گویا ”متراکم“ هستند. این یعنی میان هر دو عدد گویا، شما همیشه می‌توانید عدد گویای دیگری را پیدا کنید. هیچ یک از دستگاه‌های ℕ یا ℤ چنین خاصیتی را ندارند. مثلاً میان 11 و 12 هیچ عدد طبیعی دیگری وجود ندارد. یا میان -106 و -107 هیچ عدد صحیح دیگری وجود ندارد. ولی هر چند اختلاف میاد دو عدد گویا مثل و بسیار اندک و در حدود 1 به 16 تریلیون است، ولی حداقل می‌توان یک عدد گویای دیگر را میان آنها پیدا کرد. به سادگی می‌توان اثبات کرد که میان دو عدد گویا تعداد بی‌نهایتی از اعداد گویای دیگر وجود دارند، زیرا با این فرض که میان هر دو عدد گویا یک عدد گویای دیگر وجود دارد، شما می‌توانید این عدد میانی را با عدد سمت چپ یا عدد سمت راست آن در نظر بگیرید، و معلوم است که میان آنها نیز می‌توان یک عدد گویای دیگر را پیدا کرد، و با ادامه همین روند، شما تعداد بی‌نهایتی از اعداد را حاصل خواهید کرد که میان دو عدد اولیه وجود دارند. معنی لغت ”متراکم“ نیز بر همین مورد دلالت دارد.

به دلیل اینکه ℚ خاصیت متراکم بودن دارد، می‌توان آن را بصورت یک خط پیوسته نشان داد که از سمت چپ و راست تا بی‌نهایت امتداد دارد. هر عدد گویا روی این خط دارای یک جایگاه است.

شکل3: خانوااده اعداد گویا، یا ℚ. (نکته: از همین شکل می‌توان برای نمایش خانواده اعداد حقیقی، یا ℝ ، نیز استفاده کرد).

آیا می‌بینید که چگونه شکاف‌های میان اعداد صحیح در شکل بالا پر شده است؟ میان هر دو عدد صحیح، مثل 3 و 4، تعداد بی‌نهایتی از اعداد گویا بصورت متراکم وجود دارند.

بخاطر داشته باشید که عروسک‌های روسی بصورت تو در تو در داخل یکدیگر قرار می‌گیرند. ℚ شامل ℤ است و ℤ شامل ℕ. روش دیگری که می‌توان به این مورد نگاه کرد به این صورت است: یک عدد طبیعی یک عدد صحیح نیز هست، و یک عدد صحیح (که شامل اعداد طبیعی هم می‌شود)، یک عدد گویا نیز می‌باشد. شما می‌توانید با اضافه کردن یک علامت مثبت به اعداد طبیعی (مثلاً +12)، آنها را صریحاً در قالب اعداد صحیح بیان کنید، یا با دادن یک مخرج 1 به اعداد صحیح، آنها را صریحاً به شکل اعداد گویا بیان کنید (مثل ).

3

انواع دیگری از اعداد نیز وجود دارند، که نه صحیح هستند و نه گویا. این اعداد حدود 500 سال قبل میلاد توسط یونانی‌ها کشف شدند. این کشف تاثیر عمیقی روی طرز فکر یونانی‌ها گذاشت و سئولاتی را مطرح کرد که پاسخ‌های داده شده به آنها حتی امروز نیز برای همه ریاضیدانان و فیلسوفان رضایت‌بخش نیست.

ساده‌ترین نمونه از چنین اعدادی ریشه دوم عدد 2 است، که امروزه آن را بصورت نشان می‌دهیم. این عددی است که اگر آن را در خودش ضرب کنید حاصل آن 2 خواهد بود. اگر بخواهیم این عدد را بصورت هندسی بیان کنیم، این عدد طول قطر یک مربع می‌باشد که طول اضلاع آن 1 است. به آسانی می‌توان نشان داد که این عدد نمی‌تواند هیچ عدد گویایی باشد. استدلال مشابهی نشان می‌دهد که اگر N یک توان kام کامل نباشد،kامین ریشه N یک عدد گویا نیست.

واضح است برای شامل کردن این اعداد غیر-گویا (irrationals)، ما به یک عروسک روسی بزرگتر نیاز داریم. این عروسک جدید، دستگاه اعدادِ حقیقی نام دارد و آن را با1/4/1401 ℝ نشان می‌دهیم. ریشه دوم 2، یک عدد حقیقی است، ولی یک عدد گویا نیست. این عدد در ℝ هست ولی در ℚ نیست (و واضح است که در ℤ یا ℕ هم قرار ندارد).

مانند اعداد گویا، اعداد حقیقی هم متراکم هستند. میان هر عدد حقیقی، شما همیشه می‌توانید عدد حقیقی دیگری را پیدا کنید. به دلیل اینکه اعداد گویا خودشان از قبل متراکم هستند، ممکن است شما متعجب شوید که چگونه اعداد حقیقی می‌توانند میان آنها فشرده شوند. واقعیت عجیب‌تری که در اینجا وجود دارد این است که ℤ و ℚ هر دو قابل‌شمارش (countable) هستند ولی ℝ چنین خاصیتی را ندارد. یک مجموعه قابل شمارش مجموعه‌ای است که شما بتوانید هر یک از اعضای آن را با مجموعه اعداد شمارشی (ℕ)، یعنی یک، دو، سه، چهار، ...، متناظر کنید (حتی اگر لازم باشد اینکار را تا ابد ادامه دهید). چنین کاری را نمی‌توانید با ℝ انجام دهید. حسی هست که به ما می‌گوید ℝ (نسبت به ℕ، ℤ یا ℚ) ”آنقدر بزرگ“ است که نمی‌توان آن را با ℕ متناظر کرد. پس چگونه این تعدادِ اَبَربی‌نهایت از اعداد حقیقی می‌توانند در میان اعداد گویا جای بگیرند؟

این مسئله بسیار جالبی است که ناراحتی فراوانی را برای ریاضیدانان فراهم آورده. این مسئله به تاریخ جبر مربوط نیست، و فقط به دلیل اینکه در طول این کتاب چند بار به موضوع شمارش پذیری اشاره می‌شود (بخش‌های 14.3 و 14.4)، من آن را در اینجا مطرح کردم. کافیست بگویم که نموداری که برای نمایش ℝ از آن استفاده می‌شود، همان است که برای نمایش ℚ از آن استفاده کردیم، یعنی یک خط پیوسته، که تا بی‌نهایت از چپ و راست ادامه دارد. هنگامی که برای نمایش ℝ از این خط استفاده می‌شود، به آن ”خط حقیقی“ گفته می‌شود. اگر بخواهیم انتزاعی‌تر صحبت کنیم، ”خط حقیقی“ را می‌توان بعنوان مترادفِ ℝ درنظر گرفت.

4

ما همیشه می‌توانیم در درون ℕ جمع و ضرب را انجام دهیم، ولی فقط در برخی موارد می‌توانیم تفریق و تقسیم انجام دهیم. در درون ℤ، ما همیشه می‌توانیم جمع، ضرب، و تفریق را انجام دهیم، ولی فقط در برخی موارد می‌توانیم تقسیم انجام دهیم. در درون ℚ، ما همیشه می‌توانیم جمع، ضرب، تفریق، و تقسیم را انجام دهیم (به غیر از تقسیم بر صفر)، ولی اینجا نیز هنگام ریشه گرفتن با مشکل مواجه می‌شویم.

اگر ℝ را بکار بگیریم، مشکل ریشه گرفتن از اعداد مثبت برای ما حل می‌شود. بخاطر دارید که طبق قاعده علامت‌ها، هر عددی که در خودش ضرب شود (چه مثبت باشد چه منفی)، حاصل آن یک عدد مثبت خواهد بود. به عبارت دیگر، اعداد منفی هیچ ریشه دومی در ℝ ندارند.

از قرن شانزدهم میلادی به این سو، این محدودیت موجب ناراحتی ریاضیدانان بود، بنابراین عروسکِ روسی جدیدی ابداع شد که در آن اعداد منفی نیز ریشه دوم داشته باشند. این عروسک جدید، دستگاه اعدادِ مختلط (complex numbers) نام گرفت، که آن را با ℂ نشان می‌دهند. در درون این دستگاه جدید، کلیه اعداد، چه مثبت و چه منفی، دارای ریشه دوم هستند. ثابت شده که شما می‌توانید کُل این دستگاه را با استفاده از اعداد حقیقی معمولی، و تنها با اضافه کردن یک عدد جدید، بسازید. این عدد جدید است که همیشه آن را با i نشان می‌دهند. مثلاً ریشه دوم -25 برابر 5i است، زیرا 5i×5i=25×(-1)، که همان -25 است. درباره ریشه دوم خود i چطور؟ هیچ مشکلی نیست. اگر شما قاعد ساده ضرب پرانتزها را بیاد داشته باشید، می‌دانید که

(u + v)×(x + y)=ux+uy +vx+vy

بنابراین،

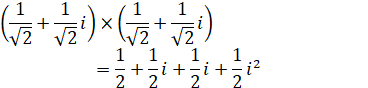
و به دلیل اینکه i²=-1 و ، طرف راست تساوی فقط مساوی i است. بنابراین ریشه دوم i برابر است.

مانند قبل، این عروسک‌ روسی جدید نیز حالتی تو در تو دارد، یک عدد حقیقی مانند x، یک عدد مختلط نیز هست، زیرا می‌توان آن را به شکل x+0i نوشت. همچنین یک عدد مختلط به شکل 0+yi، یا به اختصار yi، که در آن y یک عدد حقیقی است، یک عدد موهومی (imaginary number) نامیده می‌شود.

قواعدِ جمع، تفریق، ضرب، و تقسیم اعداد مختلط همه بر مبنای این حقیقت هستند که i²=-1. این قواعد بصورت زیر می‌باشند:

جمع: (a+bi)+(c+di)=(a+b)+(b+d)i

تفریق: (a+bi)-(c+di)=(a-b)+(b-d)i

ضرب: (a+bi)×(c+di)=(ac-bd)+(ad+bc)i

تقسیم:

به دلیل اینکه یک عدد مختلط دو جزء مستقل دارد، دستگاه ℂ را نمی‌توان بصورت یک خط نمایش داد. برای نمایش ℂ، شما به یک صفحه مسطح نیاز دارید، که در کلیه جهات به سمت بی‌نهایت می‌رود. چنین صفحه‌ای، صفحه مختلط (complex plane) نام دارد و بصورت زیر نمایش داده می‌شود. در اینجا عدد مختلطِ a+bi، توسط یک دستگاه مختصات معمولی، بصورت یک نقطه در این صفحه نمایش داده می‌شود.

شکل 4: دستگاه اعداد مختلط، یا ℂ.

توجه داشته باشید به هر عدد مختلطی که بشکل a+bi است، یک عدد مثبت بسیار مهم نسبت داده می‌شود که مقدار آن برابر است و مدول (modulus) آن عدد نامیده می‌شود. طبق قضیه فیثاغورث، از شکل بالا معلوم است که در صفحه مختلط، مدول یک عدد مختلط برابر است با فاصله آن نقطه از صفر (که مبداء نامیده می‌شود).

ما بعداً دستگاه‌های دیگری از اعداد را نیز خواهیم دید، ولی همه چیز از همین چهار دستگاهی شروع می‌شود که هر کدام به ترتیب در داخل دیگری قرار دارند: ℕ ، ℤ، ℚ، ℝ، و ℂ.

5

مفهوم مهم دیگری که من در سراسر این کتاب بارها به آن رجوع خواهم کرد چندجمله‌ای‌ها (polynomial) هستند. بنظر می‌رسد که ابتدا ریاضیدان فرانسوی فرانسوا ویت (François Vite) در قرن شانزدهم از این اصطلاح استفاده کرده باشد، و حدود صد سال بعد به زبان انگلیسی وارد شده.

چندجمله‌ای یک عبارت ریاضی است (ولی نه یک معادله که در یک سمت خودش علامت تساوی داشته باشد) و از اعداد و ”مجهولاتی“ ساخته شده که تنها با عملیاتی مثل جمع، تفریق، و ضرب با هم ترکیب شده‌اند. شما می‌توانید این عملیات را هرچقدر که بخواهید تکرار کنید، ولی نه به تعداد نامتناهی. چند مثال از چندجمله‌ای‌ها را در زیر می‌بینید:

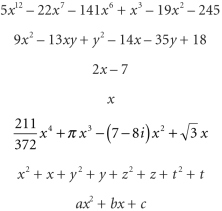
به نکات زیر توجه داشته باشید:

مجهولات: در یک چندجمله‌ای تعداد مجهولات (Unknowns) می‌تواند هر عددی باشد.

استفاده از حروف برای مجهولات: برای نمایش مجهولات واقعی، یعنی آنهایی که مقدار آنها حقیقتاً برای ما جالب است و در جستجوی آنها هستیم، معمولاً از حروف آخر الفبای لاتین استفاده می‌شوند، مثل x، y، z و برخی اوقات هم t.

توان مجهولات: بدلیل اینکه شما در یک چند جمله‌ای می‌توانید به هر تعداد متناهی که مایل باشید عمل ضرب را انجام دهید، مجهولات می‌توانند هر توانی را داشته باشند: x, x² , x³ , x²y³ , x⁵yz² , . . .

استفاده از حروف الفبا برای مفروضات: مفروضات یا ”داده‌ها“ معمولاً اعدادی هستند که از ℕ ، ℤ، ℚ، ℝ، یا ℂ گرفته شده‌اند. ممکن است ما بخواهیم از حروف استفاده کنیم تا فرمول یا عبارتی را بشکل کلی بیان کنیم. معمولاً برای اینکار از حروف اولیه الفبای لاتین (a, b, c, …) یا از حروف میانی آن (p, q, r, …) استفاده می‌شود.

ضرایب: لغت ”داده“ (Data) در بسیاری از زبان‌ها استفاده‌های خاص خودش را دارد و ما در اینجا از آن استفاده نمی‌کنیم. در یک چندجمله‌ای، ”چیزهای داده شده“ ضرایب (coefficients) نامیده می‌شوند. در سومین مثالی که در بالا از چندجمله‌ای‌ها ذکر کردم، ضرایب آن عبارتند از 2 و -7. ضرایب چهارمین چندجمله‌ای (که تنها یک جمله دارد) 1 است. ضرایب آخرین چندجمله‌ای a، b، و c است.

6

چندجمله‌ای‌ها تنها زیر مجموعه کوچکی از عباراتِ ممکنِ ریاضی را تشکیل می‌دهند. اگر آنها را بر هم تقسیم کنید، کلاس بزرگتری از عبارات را خواهید داشت که عبارات گویا نامیده می‌شوند، مانند عبارت زیر:

که یک عبارت گویا با سه مجهول است. این یک چندجمله‌‌ای نیست. شما می‌‌توانید مثلاً با ریشه گیری، گرفتن سینوس و کسینوس، یا لگاریتم، دامنه عبارات را باز هم گسترده‌‌تر کنید. دراینصورت، عباراتی را خواهید داشت که آنها نیز چندجمله‌‌ای نیستند.

چگونه یک چندجمله‌‌ای بسازیم: تعدادی اعداد مفروض را انتخاب کنید که بتوانید صریحاً آنها را بیان کنید (مثل 17، ، π، ...) یا آنها را در قالب حروفی از ابتدا یا میانه الفبای لاتین پنهان کنید (a, b, c, . . . , p, q, r, . . .) آنها را با چند مجهول (x، y، z، ...) مخلوط کنید. تعداد متناهی از عملیات جمع، تفریق، و ضرب را بر روی آنها انجام دهید. حاصل کار شما یک چند جمله‌‌ای خواهد بود.

گرچه چندجمله‌‌ای‌‌ها بخش اندکی از عبارات ریاضی تشکیل می‌دهند، ولی اهمیت بسیاری را دارند. هنگامی که ریاضیدانان از صفتِ ”جبری“ استفاده می‌‌کنند، معمولاً می‌‌توان اینطور برداشت کرد که سخن آنها به چندجمله‌‌ای‌‌ها ارتباط دارد. اگر یک قضیه مربوط به جبر را بررسی کنید، حتی مواردی که در بالاترین سطوح قرار دارند، در برخی از لایه‌‌های آنها احتمالاً یک چندجمله‌‌ای را پیدا خواهید کرد. می‌‌توان ادعا کرد که چندجمله‌‌ای‌‌ها مهمترین مفهوم در جبر هستند، چه جبر قدیم و چه نوین.

فصل 1

چهار هزار سال قبل

1.1

من در مقدمه این کتاب جبر را بعنوان چرخش گرایش انسان از حسابِ خَبری به حساب استفهامی تعریف کردم. جبر نیز از همان ابتدایِ تاریخ مدون انسان شروع شد. برخی از قدیمی‌ترین متون ریاضی که برای ما شناخته شده‌اند، حاوی موضوعاتی هستند که به خوبی می‌توان آنها را جبری نامید. تاریخ این متون به 37 یا 38 قرن پیش بازمی‌گردند، و توسط کسانی نوشته شده‌اند که در بین‌النهرین و مصر زندگی می‌کرده‌اند.

در دورانی که ما زندگی می‌کنیم، چنین زمانی بسیار دور بنظر می‌رسد. حتی برای کسانی هم که در دوران یونان باستان زندگی می‌کرده‌اند، این زمان در گذشته‌های دور قرار داشته. خارج از حلقه متخصصین باستان‌شناسی، تنها دانسته‌هایی که از آن زمان‌ها در دسترس است، فقط در کتُب مذهبی یهودی و مسیحی موجودند. چنین زمانی با دنیای ابراهیم، اسحاق، یعقوب، یوسف، و شهرهای اور (Ur)، هارآن (Haran) و سدوم و غموره مصادف است. تمدنِ آن زمان شامل کُلِ حلالِ حاصل‌خیزی بود که از سرزمین‌های قابل‌کشتی امتداد می‌یافت که از شمال‌غربی خلیج‌فارس شروع می‌شد و تا دشت‌های دجله و فرات، فلات سوریه، و از فلسطین به دلتای نیل و مصر می‌رسید. کلیه مردمان این منطقه با یکدیگر آشنا بودند.

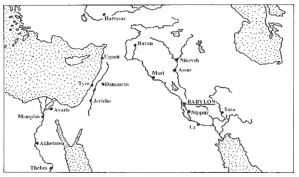
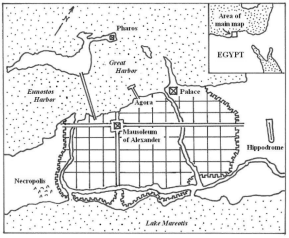
شکل 1-1: بین‌النهرین و حلال حاصل‌خیز.

در طول این حلال، از شهر اور در فرات سفلی تا تیبِز در میانه رود نیل، رفت و آمد مستمری در جریان بود.

ولی سه منطقه اصلی این حلال از لحاظ سیاسی اوضاع کاملاً متفاوتی داشتند. فلسطین ایالت عقب‌مانده‌ای بود که مردم برای رفتن به مکان‌های دیگر از آنجا عبور می‌کردند. مردمان آن روزگار، فلسطین را تحت نفوذ مصر می‌دانستند. مصر از لحاظ قومی یکدست بود و در مرزهایش دشمن جدی نداشت. در همان زمان، پیش از آنکه مردمان مصر اولین یورش خارجی را به خودشان تجربه کنند، قدمت این سرزمین از انگلستان امروزی هزار و پانصد سال بیشتر بود. مصریان باستان ذهنیتی شبیه چینی‌ها داشتند، یک سلطنت متمرکز که بر یک دستگاه دیوان‌سالارنه گسترده حکومت می‌کرد. در سلسله پنجم، که تقریباً از 2500 تا 2350 سال پیش از میلاد بر مصر حکومت می‌کردند، تقریباً 2000 عنوان رسمی وجود داشت. رابرت جی. وسون، در کتاب مراتب امپراتوری می‌گوید: ” در این سلسله مراتب شگفت‌انگیز، هر کسی با کس دیگر مساوی بود.“

در بین‌النهرین وضعیت دیگری حکم‌فرما بود. در آنجا اقوام بیشتری زندگی می‌کردند، ابتدا سومری‌ها، سپس اکدی‌ها، بعد از آن ایلامی‌ها، آموریان، هتیت‌ها، آشوریان، و آرامیان. در مواقعی که یک حکمرانِ قدرتمندِ مصری می‌توانست به سرزمین‌های بیشتری در بین‌النهرین تسلط پیدا کند، دیوان‌سالاری مستبدانه مصری نیز در آنجا بیشتر رواج می‌یافت، ولی این دوره‌های استعماری دوام زیادی نداشتند. اولین و مهمترین آنها که از 2340 ق.م تا 2189 ق.م، به مدت 160 سال بر کل بین‌النهرین حکومت کردند، دودمان آکدیِ سارگون (Sargon) بود. ولی در زمانی که به داستان ما مربوط است، یعنی قرن 18 یا 17 پیش از میلاد، عظمت ساراگون‌ها رنگ باخته بود، و تنها زبان آنها، یعنی زبان اکدی، که متعلق به خانواده زبان‌های سامی است، باقی مانده بود. سومری‌ها هنوز در جنوب پابرجا بودند و زبان آنها در میان افراد تحصیل کرده فراگیر بود، حالتی شبیه زبان یونانی برای رومیان باستان یا زبان لاتین برای اروپاییان قرون وسطی.

ولی مناطق مختلف بین‌النهرین همیشه با هم در حال ستیز بودند، و تنها چیزی که آنها را به هم پیوند می‌داد زبان و فرهنگ مشترک بود، و نه یک حکومت مرکزی مقتدر. در چنین شرایطی بود که قوه ابتکار شکوفا شد. می‌توان این را با دولت-شهرهای یونان باستان در عصر طلایی، یا رونسانس ایتالیا، یا اروپای قرن نوزدهم مقایسه کرد. آن زمان بدون شک دوران ”جالبی“ بود.

1.2

یکی از وقایع متحد کننده در بین‌النهرین که تحسین‌برانگیزتر است، از حدود 1790 ق.م تا 1600 ق.م اتفاق افتاد. کسی که این متحد سازی را انجام داد همورابی (Hammurabi) بود، که در ابتدای همان دوران در دولت-شهر بابل به قدرت رسید. همورابی یک آموری (Amorite) بود، که به یکی از لحجه‌های زبان آکدی سخن می‌گفت. او کُل بین‌النهرین را تحت حکمرانی خودش در آورد و بابِل (Babylon) را به بزرگترین شهر دوران خودش بدل کرد. این نخستین امپراتوری بابِلی بود.

امپراتوری اولِ بابِل تمدنی بود که اسناد را بخوبی ثبت می‌کرد. سبک نوشتن آنها به خط میخی بود. حروف خط میخی با فشار دادن قلم‌های گوه مانند در لوح‌های سفالی نوشته می‌شد. به منظور ثبت دائمی اسناد، این لوح‌ها و استوانه‌های سفالی نگهداری می‌شدند. خط میخی خیلی پیش از اینکه توسط آکدها در دوران سارگون مورد استفاده قرار گیرد، توسط سومری‌ها اختراع شده بود. در زمان همورابی این سبک از نوشتن به دستگاهی با 600 علامت تبدیل شد، که هر کدام یکی از هجاهای آکدی را نمایش می‌داد.

در زیر جمله‌ای را می‌بینید که به خط میخی آکدی در مقدمه قوانین حمورابی نوشته شده. اینها شامل قوانین مهمی بودند که حمورابی آنها را در سراسر امپراتوری خودش اعمال کرده بود.

شکل 2-1: نمونه‌ای از خط میخی در قوانین حمورابی.

نوشته تقریباً اینطور تلفظ می‌شود ”اِن-لیل بعل سا-مه اُ اِر-ستیم“، که یعنی ”انلیل خداوندگار آسمان و زمین“. با نگاه به لغت بعل می‌توان فهمید که این زبان یکی از زبان‌های سامی است، که مثلاً نمود آن را در لغت عبری بعلزبوب، به معنای شیطان بزرگ، است، که در زبان انگلیسی به شکل (Beelzebub) نوشته می‌شود.

در واقع قرن‌ها بعد از سقوط امپراتوری بابل، هنوز خط میخی تا قرن دوم پیش از میلاد رواج داشت. از این خط برای نوشتن خیلی از زبان‌های باستانی استفاده می‌شد. در بسیاری از خرابه‌های ایران، کتیبه‌های زیادی وجود دارند که به خط میخی نوشته شده‌اند، که به دوران کورش کبیر، یعنی به قرن پنجم پیش از میلاد بازمی‌گردد. اروپاییانی که در قرن پانزدهم از ایران بازدید می‌کردند متوجه این کتیبه‌ها شدند. در اواخر قرن هجدهم میلادی، دانشوران اروپایی شروع به خواندن این کتیبه‌ها کردن، و تقریباً در اواسط قرن نوزدهم، اصول خط میخی به میزان زیادی رمزگشایی شده بود.

در همان زمان‌ها، باستان شناسانی نظیر پُل امیل بوتا، و سِر آستن هنری لایارد شروع به حفاری بسیاری از نقاط باستانی بین‌النهرین کردند. در میان چیزهای که آنها کشف کردند، تعداد زیادی از لوح‌های سفالی پخته شده قرار داشت که همه به زبان میخی بودند. این کارهای باستان‌شناسی تا به امروز ادامه دارند، و ما تقریباً نیم میلیون از این الواح را در دست داریم که در موزه‌ای عمومی یا خصوصی در سراسر جهان نگهداری می‌شوند، و تاریخ آنها شامل یک محدوده سه‌هزار و سیصد ساله می‌شود، یعنی از ابتدای کتابت، در 3350 سال پیش از میلاد، تا قرن اول پیش از میلاد. تعداد زیادی از لوح‌های کشف شده به دوران حمورابی مربوط هستند.

1.3

از همان ابتدا (حداقل از دهه 1860 به بعد) معلوم بود که برخی از لوح‌های میخی حاوی اطلاعات عددی هستند. اولین لوح‌هایی که رمز آنها کشف شد به ثبت امور اداری و بازرگانی مربوط بودند: فهرست دارایی‌ها، حساب‌ها، و از این قبیل. موارد زیادی از اطلاعات نیز وجود دارند که به گاه‌شماری مربوط هستند. بابِلیان گاه‌شماری پیچده و دانش وسیعی از نجوم داشتند.

ولی در اوایل قرن بیستم تعداد زیادی از الواح کشف شدند که گرچه حاوی اطلاعات عددی بودند، ولی این اطلاعات نه به گاه‌شماری و نه حسابداری، بلکه به ریاضیات مربوط بود. تا زمانی که اتو نویگی‌باوئر (Otto Neugebauer) در 1929 این الواح را بررسی نکرد، محتوای آنها بطور دقیق مورد مطالعه قرار نگرفته بود.

نویگی‌باوئر یک ریاضیدان اطریشی بود که در 1899 متولد شد. او در جنگ جهانی اول خدمت کرد، و به همراه یکی دیگر از هم‌وطنان خودش، فیلسوف معروف لودویگ ویتگنشتاین (Ludwig Wittgenstein)، از یک اردوگاه جنگی سر درآوردند. او پس از جنگ ابتدا فیزیک، و پس از آن زیر نظر برخی از بهترین ریاضیدانان قرن بیستم، کسانی مانند ریچارد کورانت (Richard Courant)، ادموند لاندو (Edmund Landau)، و امی نوتر (Emmy Noether)، به تحصیل ریاضیات پرداخت. در اواسط دهه 1920، توجه نویگی‌باوئر به ریاضیات دنیای باستان جلب شد. او به مطالعه مصر باستان پرداخت و مقاله‌ای را در مورد پاپیروس رایند (Rhind Papyrus) منتشر کرد، که من بعداً درباره آن بیشتر توضیح خواهم داد. سپس به بابِلیان باستان روی آورد، زبان آکدی یاد گرفت، و شروع به مطالعه الواح بجا مانده از دوره حمورابی نمود. حاصل اینکار اثر پرباری بنام (Mathematische Keilschrift-Texte)، یا متونِ ریاضی میخی بود که طی سالهای 1937-1935، در سه جلد منتشر شد. در این اثر برای اولین بار ارزش ریاضیات بابلی نشان داده شد.

گرچه نویگی‌باوئر یهودی نبود، ولی از لحاظ سیاسی آزادی‌خواه بود و هنگامی که نازی‌ها به قدرت رسیدند آلمان را ترک کرد. به دنبال پاکسازی موسسه ریاضی گوتینگن از یهودی‌ها، او بعنوان رئیس این موسسه برگزیده شد. مورخ ریاضی، کُنستنس رِید (Constance Reid) در کتاب خودش بنام هیلبرت می‌گوید ”او تنها یک روز عهده دار این سمت بود، زیرا حاضر نشد علامیه وفاداری را امضاء کند.“ نویگی‌باوئر ابتدا به دانمارک و سپس به ایالات متحده رفت، جایی که او به مجموعه‌های جدیدی از الواح میخی دسترسی پیدا کرد. او در 1945 به همراه آشور-شناس آمریکایی آبراهام زاکس کتاب متون ریاضی میخی را به زبان انگلیسی منتشر کرد، که یک کتاب مرجع درباره ریاضیات دوران بابِل باستان محسوب می‌شود. البته پس از آن نیز تحقیقات ادامه یافت و حالا نبوغ ریاضی بابِلی بر همگان معلوم است. خصوصاً حالا ما می‌دانیم که آنها بر تکنیک‌هایی مسلط بودند که حقیقتاً می‌توانیم آنها را جبری بنامیم.

1.4

نویگی‌باوئر کشف کرد که متون ریاضی دوران حمورابی بر دو نوع هستند: ”متونِ جدولی“ و ”متونِ مسئله‌ای“. متونِ جدولی فقط شامل یک سری از جداول، مثل جدول ضرب، جدول مربعات و مکعبات، و برخی دیگر از فهرست‌های پیشرفته‌تر مثل جدول شماره 322 پیلیمتون بودند،که حالا در دانشگاه ییل نگهداری می‌شود و فهرستی از سه‌گانه‌های فیثاغورثی را در خود دارد. (سه‌گانه‌های فیثاغورثی اعدادی به شکل a,b,c هستند که میان آنها رابطه a²+b²=c² برقرار است، و همچنین طبق قضیه فیثاغورث، اندازه اضلاع یک مثلث قائم‌الزاویه هستند.)

بابلیان برای دستگاه‌ عدد نویسی خودشان، به چنین جداولی نیاز مبرم داشتند. باوجود اینکه دستگاه عدد نویسی آنها پیشرفته بود، ولی مانند دستگاه فعلی ما بر مبنای 10 قرار نداشت، بلکه بر مبنای 60 بود. همانطور که ”37“ در مبنای 10 به معنی سه ده‌تا بعلاوه هفت است، اگر همین عدد در مبنای 60 خوانده شود، آنگاه به معنای سه شصت‌ تا بعلاوه هفت، یا به عبارتی 187 خودمان خواهد بود. به دلیل اینکه در آن زمان هنوز صفر اختراع نشده بود، انجام عملیات حساب خیلی مشکل بود. (صفر همان علامت مفیدی است که مثلاً به ما اجازه می‌دهد میان اعداد 284, 2804, 208004 و غیره تفاوت قایل شویم).

کسور به شکل ساعت‌ها، دقایق، و ثانیه‌ها نوشته می‌شدند، که همه آنها یادگار بابِلیان هستند[2]. در این دستگاه، عددی مثل ”دو و نیم“ را می‌توان به شکل ”2:30“ نمایش داد. بابلیان می‌دانستند که ریشه عدد 2 در دستگاه آنها تقریباً برابر ”1:24:51:10“ است، یعنی 1 + (24 + (51 + 10 ÷ 60) ÷ 60) ÷ 60، که تا شش رقم اعشار درست است.

داشتن یک ذهنیت جبری حتی در متون جدولی بابلی نیز مشهود است. برای نمونه، ما می‌دانیم که برای انجام ضرب می‌توان از جداول مربع استفاده کرد. مثلاً فرمول زیر می‌تواند ضرب را به یک تفریق (و یک تقسیم ساده) کاهش دهد.

بابلیان این فرمول را می‌دانستند (البته اگر فرمول برای آنها معنی داشت، زیرا آنها هیچ راهی برای برای بیان این فرمولِ انتزاعی نداشتند). بهتر است بگوییم آنها رویه این محاسبه را می‌دانستند (چیزی که ما امروزه به آن الگوریتم algorithm می‌گوییم)، و می‌توانستند آن را بر روی اعداد خاصی بکار بگیرند.

1.5

الواحِ جدولی به نوبه خودشان جالب هستند، ولی ما الواحی را داریم که شامل یک سری مسئله هستند که شروع جبر را در آنها می‌بینیم. آنها مثلاً حاوی روش‌هایی برای حل معادلات درجه دوم یا حتی انواع خاصی از معادلات درجه سوم هستند. واضح است که هیچ‌کدام از اینها به شکلی که ما امروز می‌شناسیم، توسط نمادگذاری‌های جبری بیان نشده بودند. همه کارهایی که در این نوع مسائلِ لفظی انجام می‌شد، فقط شامل اعداد واقعی بودند.

برای اینکه تا حدی مزه ریاضیات بابلی را به شما نشان دهم، یکی از مسائل کتاب کتاب نویگی‌باوئر را به سه شکل برای شما مطرح خواهم کرد: متن میخی اولیه، ترجمه تحت‌الفظی، و نمایش امروزی مسئله.

متن میخی اصلی در شکل 3-1 نمایش داده شده. این متن بر دو طرف لوحی نوشته شده که من آنها را در کنار هم نمایش داده‌ام.

نویگی‌باوئر و زاکس این لوحه را ترجمه کردند. قسمت‌هایی که به حروف ایتالیک نمایش داده شده‌اند آکدی هستند؛ جملات ساده سومری هستند؛ آنچه در کروشه آمده آنهایی هستند که واضح نیستند یا ”درست فهمیده نشده‌اند.“

شکل 3-1: یک لوحِ مسئله‌ای که به خط میخی نوشته شده.

(توجه: در اینجا نویگی‌باوئر و زاکس از کاما برای جدا کردن ارقام اعداد استفاده کرده‌اند، و از سِمی‌کلون برای جدا کردن قسمت صحیح و کسری یک عدد. بنابراین ”1,12;15“ یعنی ، که می‌شود ).

(تصویر سمت چپ)

[ایگبوم] به میزان 7 از ایگوم بیشتر است.

مقدار [ایگوم] و ایگبوم چه هستند.

مقداری که ایگبوم از ایگیب بیشتر است (یعنی 7) را نصف کن، که حاصل آن 3;30 است.

3;30 را در 3;30 ضرب کن، که حاصل آن 12;15 است.

به آن 12;15 که بدست آوردی مقدار 1,0 را اضافه کنن که نتیجه آن 1,12;15 است.

ریشه دوم 1,12;15 چیست؟ (جواب) 8;30 است.

8;30 را کنار بگذار، و سپس

(تصویر راست)

3;30 را از این مقدار کم کن.

آن را با دیگری جمع کن.

یکی 12، و دیگری 5 است.

ایگبوم 12، و ایگوم 5 است.

حالا این مسئله را به زبان امروزی بیان می‌کنیم:

عددی به میزان 7 از معکوس خودش بیشتر است، آن عدد چیست؟ ولی توجه داشته باشید چون در عدد نویسی بابلی مفهوم ”جایگاه-مقدار“ مبهم است، ”وارونه عدد x“ می‌تواند به معنی ، یا ، یا ...، یا در واقع هر توانی از 60 که بر x تقسیم شود، باشد. ولی از حلی که نویسنده مسئله ارائه داده می‌توان برداشت کرد که منظور او بوده. بنابراین

پس x و وارون آن چه اعدادی هستند؟

به دلیل اینکه معادله فوق به معادله درجه دوم زیر ساده می‌شود

x²-7x-60=0

ما می‌توانیم برای حل آن از فرمول معروف معادله درجه دوم استفاده کنیم:

که به ما دو عدد x=12 و x=-5 را می‌دهد. بابلیان هیچ چیزی درمورد اعداد منفی، که حدود 3000 سال بعد از آنها اختراع شد، نمی‌دانستند. از نظر آنها، تنها جواب مسئله 12، و معکوس آن 5 (یعنی ) است. در واقع راه‌حلی که آنها از آن استفاده می‌کردند، آن دو جوابی که فرمول معادله درجه دوم به ما می‌دهد را نمی‌دهد، ولی معادل فرمولی است که کمی با آن متفاوت، و بصورت زیر است:

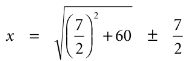
با اینحال، شما هنوز باید قبول کنید که این دستاورد بسیار شگفت‌انگیزی برای ریاضیات عصر مفرغ است.

1.6

بار دیگر تاکید می‌کنم که بابلیان عصر حمورابی از هیچ نمادگذاری جبری استفاده نمی‌کردند. مسائل آنها فقط بصورت لفظی نوشته می‌شد، که در آن کمیت‌های مورد نظر با استفاده از یک دستگاه عددی بَدوی بیان می‌شدند. آنها برای یافتن ”کمیت مجهول“، تنها یک یا دو قدم بر می‌داشتند و در متون آکدی خودشان از لغات سومری استفاده می‌کردند (مثل ایگوم و ایگبوم در مسئله بالا). نویگی‌باوئر و زاکس، هم ایگوم و هم ایگبوم را به معنی معکوس و وارون ترجمه کرده‌اند. ولی در لوحه‌های دیگر سومری آنها از ”طول“ و ”عرض“ استفاده می‌کنند، که به یک مستطیل مربوط هستند. الگوریتم‌های مورد استفاده حالتی عمومی نداشتند، و برای مسائل لفظی مختلف از الگوریتم‌های متفاوت استفاده می‌شد.

اینجا دو سئوال مطرح می‌شود. اول اینکه چرا آنها به خودشان زحمت چنین کارهایی را می‌دادند؟ و دوم، چه کسی ابتدا به چنین راه‌حل‌هایی پی برد؟

درمورد سئوال اول باید گفت که آنها فکر نمی‌کردند لازم باشد به ما بگویند چه می‌کردند. بهترین حدسی که می‌توانیم دراینمورد بزنیم این است که این مسائلِ لفظی هنگامی پیش می‌آمدنند که آنها می‌خواستند صحت محاسبات خودشان را بررسی کنند، مثلاً محاسبات مربوط به اندازه‌گیری مساحت زمین‌ یا سئوالات مربوط به خاک‌برداری. هنگامی که یک زمین چهار‌گوش علامتگذاری و مساحت آن محاسبه شد، شما می‌توانستید به طریق ”معکوس“ از این الگوریتم‌ها استفاده کرده و مطمئن شوید جوابی که بدست آورده‌اید صحیح است.

در مورد سئوال دوم، باید بگویم که جبر-اولیه که در لوحه‌های دوران حمورابی آمده است، حالتی بالغ دارد. بر اساس آنچه ما از سرعتِ پیشرفتِ فکری بشر در گذشته‌های دور می‌دانیم، این تکنیک‌ها باید در طول چندین قرن به بلوغ رسیده باشند. چه کسی ابتدا آنها را ابداع کرد؟ این چیزی است که خیلی معلوم نیست، هرچند استفاده از زبان سومری در این لوحه‌ها بر این دلالت دارد که آنها منشاء سومری دارند. (مثلِ استفاده از حروف یونانی در ریاضیات نوین، که از قدمت آن تا زمان یونان باستان حکایت می‌کند.) ما لوحه‌هایی را داریم که به پیش از دوران حمورابی تعلق دارند، و قدمت آنها به هزاره سوم پیش از میلاد بازمی‌گردد، ولی همه آنها فقط حسابی هستند. تفکرِ جبری فقط در دوره حمورابی، یعنی قرون 18 و 17 پیش از میلاد، ظاهر می‌شود. اگر متون و الواحی وجود داشته‌اند که به ”حلقه‌های گمشده‌ای“ دلالت داشته باشند، حالا دیگر چیزی از آنها باقی نمانده، یا هنوز پیدا نشده‌اند.

الواح دوران-حمورابی نیز چیزی مبنی براینکه چه کسانی آنها را نوشته‌اند به ما نمی‌گویند. ما مطالب بسیاری درباره ریاضیات بابِلی می‌دانیم، ولی با اینحال هیچ ریاضیدان بابلی را نمی‌شناسیم. اولین کسی که نام او را می‌دانیم، و به احتمال زیاد یک ریاضیدان بوده، در سوی دیگر این حلال حاصلخیز زندگی می‌کرد.

1.7

در زمانی که سلسله حمورابی در بین‌النهرین مشغول استحکام قدرت خودش بود، مصر با اولین تهاجم خارجی مواجه شد. مردمان مهاجم کسانی بودند که یونانیان آنها را هیک‌ساس (Hyksos) می‌نامیدند، که اگر بخواهیم بصورت تحت‌الفظی لغت هیک‌ساس را از مصری ترجمه کنیم، به معنای ”فرمانروایان سرزمین‌های خارجی“ است. آنها در حدود 1720 سال پیش از میلاد، در حوالی شرقی دلتای نیل، در شهر آواریس (Avaris) پایتخت خودشان را بنا کردند.

در زمان سلسله هیک‌ساس، مردی بنام احمِس (Ahmes) زندگی می‌کرد. چیزی که احمِس را از بقیه متمایز می‌کند این است که او اولین کسی است که ارتباط معینی با ریاضیات دارد. ما از طریق یک پاپیروس، که تاریخ نوشتن آن به 1650 سال پیش از میلاد، یعنی در اوایل سلسله هیک‌ساس، باز می‌گردد، با نام او آشنا هستیم. احمس در آن پاپیروس به ما می‌گوید که او کاتبی است که مشغول کپی کردن یک سند است که به دودمان دوازدهم تعلق دارد (در حدود 1990 تا 1780 سال ق.م). شاید این کپی‌برداری یکی از پروژه‌های حفظ متون قدیمی باشد که توسط حکمرانان هیک‌ساس انجام می‌گرفت و ما از آن اطلاع داریم. شاید احمس چیزی از ریاضیات نمی‌دانست و تنها مشغول نسخه برداری از چیزی بود که آن را به وی قرار داده بودند. در آن پاپیروس برخی از خطاهای ریاضی وجود دارد، و آنچه بچشم می‌خورد بیشتر شبیه خطاهای محاسباتی هستند تا اشتباهات نوشتاری (مثلاً از اعداد اشتباهی استفاده شده).

بدلیل اینکه جهانگردی بنام هنری ریند این پاپیروس را پیدا کرد، حالا این سند به پاپیروس ریند (Rhind Papyrus) معروف شده. ریند این پاپیروس را در شهر لوکسور (اقصر) مصر خرید. هنگامی که ریند پنج سال بعد فوت شد، موزه بریتانیا به آن دست یافت. بهتر است این پاپیروس را بنام مردی که آن را نوشته نامگذاری کنیم تا مردی که آن را خریداری کرده. بنابراین امروزه آن را پاپیروس احمس می‌نامند.

هر چند از لحاظ ریاضی پاپیروسِ احمس یافته‌ای بسیار گیرا و مهم است، ولی تنها حاوی مقدار اندکی از تفکر جبری می‌باشد. در اینجا به مسئله 24 آن اشاره می‌کنم که مهمترین نکته جبری در این پاپیروس است. ”کمیتی با یک‌چهارم خودش جمع، و حاصل آن 15 شده.“ اگر آن را بطورت امروزی بنویسیم، معادله‌ای به شکل زیر را خواهیم داشت:

برای حل این معادله و یافتن کمیت مجهول، حامس از روش سعی-و-خطا استفاده کرده. روش‌های اصولی و الگوریتمی اندکی در این پاپیروس به چشم می‌خورد.

1.8

جیمز آر. نیومن (James R. Newman) در کتاب دنیای ریاضیات می‌نویسد: ”در میان دانشجویان علومِ باستانی نظرات متفاوتی درباره قابلیت‌های ریاضیاتِ مصری وجود دارد.“ ظاهراً هنوز این تفاوت باقیست. ولی وقتی من به متون بابِلیان و مصریان باستان نگاه می‌کنم، تصور نمی‌کنم کسی بتواند انکار کند این دو تمدنی که در نیمه هزاره دوم قبل از میلاد، در دو سوی حلالِ حاصل‌خیز شکوفا شدند، از لحاظ ریاضی باهم برابر بودند. هرچند هر دو آنها به روش محاسباتی کار می‌کردند، و از لحاظ قدرت‌های تجریدی شواهد اندکی برای کارهای آنها وجود دارد، مسائلی که بابِلیان مطرح می‌کردند، نسبت به مصریان عمیق‌تر و ظریف‌تر بود. (نویگی‌باوئر نیز همین عقیده را دارد.)

چیزی که هنوز خارق‌العاده بنظر می‌رسد این است که این مردمان باستانی، چگونه با روش عدد نویسی بدوی خودشان توانسته بودند به چنین پیشرفتهایی دست پیدا کنند. چیزی که جای شگفتی بیشتری دارد این است که چرا در قرن‌های آتی پیشرفت آنها متوقف شد و دست‌آوردهای بسیار اندکی را حاصل کردند.

فصل 2

پدر جبر

2.1

دیافانتوس (Diophantus)، که من این فصل را به افتخار او نام‌گذاری کرده‌ام، در دوران حکومت رومی‌ها بر مصر، در قرن یکم، یا دوم، یا سوم بعد از میلاد در شهر اسکندریه زندگی می‌کرد.

اینکه آیا دیافانتوس واقعاً پدر جبر بود یا نه، جای بحث دارد. بسیاری از مورخان معتبر ریاضی این را رد می‌کنند. برای مثال کورت ووگل (Kurt Vogel) کارهای دیافانتوس را همانقدر جبری می‌داند که کارهای بابِلیان باستان یا ارشمیدس را، و نتیجه می‌گیرد که ”دیافانتوس آنطور که غالباً معروف است، قطعاً پدر جبر نیست.“ مورخ هلندی، وان در واردن (Van der Waerden) به دوره‌های بعدی اشاره می‌کند، و از خوارزمی (al-Khwarizmi) که 600 سال بعد از دیوفانتوس می‌زیست بعنوان پدر جبر یاد می‌کند. این چیزی است که من در فصل بعد درمورد آن توضیح خواهم داد. علاوه‌براین، امروزه شاخه‌ای از ریاضیات وجود دارد که آنالیز دیوفانتی (Diophantine analysis) نامیده می‌شود و غالباً بعنوان درسی در نظریه اعداد، (ولی نه جبر) به دانشجویان آموخته می‌شود.

من به کارهای دیافانتوس اشاره خواهم کرد، و قضاوت در این مورد را به خود شما واگذار می‌کنم. بعداً نظر خودم را بعنوان یک نتیجه‌گیری ابراز خواهم کرد.

2.2

تا زمانی که در سال 141 پیش از میلاد پارت‌ها (اشکانیان) بین‌النهرین را فتح نکرده بودند، مردمان آن سرزمین برای قرن‌ها به نوشتن به خط میخی ادامه دادند. ما متون ریاضی را داریم که درست به پیش از این فتح تعلق دارند. بنابر گواهی تمام کسانی که این موضوع را مطالعه کرده‌اند، آنها با کمال تعجب تصدیق می‌کند که در هزار و پانصد سالی که میان امپراطوری حمورابی تا فتح اشکانیان فاصله داشت، تقریباً هیچ پیشرفتی در نمادگذاری ریاضی، تکنیک‌ها، یا فهم بیشتر موضوعات مربوطه حاصل نشد. ریاضیدان معروف، جان کانوی (John Conway) که لوحه‌های میخی را مطالعه کرده، می‌گوید تنها تفاوتی که خودش را نشان می‌دهد، استفاده از ”صفر مکانی“ است که در لوحه‌های اخیر به چشم می‌خورد (یعنی راهی که توسط آن مثلاً می‌توانیم بین 281، 2801 تفاوت قائل شویم). مانند بین‌النهرین، در مورد مصر نیز ما نمی‌دانیم که چرا میان قرون 16 تا 4 ق.م، ریاضیات هیچ پیشرفت قابل‌توجهی نداشت.

با وجود اینکه که ریاضیدانان مصری یا بابِلی در سرزمین‌های خودشان هیچ پیشرفتی حاصل نکردند، اما کشفیاتِ آغازین و شگف‌انگیز آنها به سمت غربِ باستان ، و احتمالاً فرای آن، گسترش پیدا کرد. از این نقطه به بعد (در واقع از قرن ششم ق.م) داستان جبر در جهان باستان، صرفاً یک داستان یونانی است.

2.3

ویژگی ریاضیات یونانی این است که تا پیش از دیافانتوس بیشتر جنبه هندسی داشت. دلیلی که معمولاً برای این مورد ارائه می‌شود، و به نظر من محتمل بنظر می‌رسد، این است که مکتب فیثاغورثیان (که در آواخر قرن ششم ق.م تاسیس شده بود) این ایده را داشت که کُل ریاضیات (و موسیقی، و نجوم) بر پایه اعداد بود، ولی کشف اعداد غیرگویا (یا گنگ)، چنان برای آنها نارحت کننده بود که توجه خودشان را از حساب، که بنظر می‌رسید حاوی اعدادی بود که نمی‌شد آنها را به شکل اعداد کسری نوشت، به هندسه معطوف کردند، که می‌شد همه اعداد را به صورتِ طولِ پاره‌خط‌ها نشان داد.

بنابراین، مفاهیم جبری یونانی به شکل هندسی بیان می‌شدند، که غالباً مبهم بودند. مثلاً، باشماکووا و اسمیرنوا به این اشاره می‌کنند که قضایای 28 و 29 کتاب اصول اقلیدس، روشی برای حل معادلات درجه دوم ارائه می‌دهند. من فرض را بر این می‌گیرم که چنین چیزی درست است، ولی چنین چیزی در نگاه اول واضح نیست.

اقلیدس در شهر اسکندریه مصر می‌زیست و در زمانی که بقیه مصر تحت حکمرانی سردار نظامی اسکندر، یعنی بطلميوس بود، در آنجا مدرسه‌ای را تاسیس کرد و مشغول به تدریس شد. البته مدت کوتاهی پیش از اینکه اقلیدس متولد شود، خود شهر اسکندریه توسط اسکندر پایه‌گذاری شده بود. اسکندریه جایی در طول مدیترانه به طرف یونان بود که در کرانه غربی دلتای نیل قرار داشت. گمان برده می‌شود که خود اقلیدس پیش از اینکه در مصر مستقر شود، آموزش‌های ریاضی خود را در شهر آتن، و در مکتب افلاطون گذرانده باشد. در هر حال، اسکندریه در قرن سوم ق.م مرکز مهمی برای ریاضیات بود، که حتی از خود یونان هم مهمتر بود.

اقلیدس حوالی 300 ق.م.

ارشمیدس (Archimedes) که 40 سال جوانتر از اقلیدس بود، و احتملاً زیر نظر شاگردان اقلیدس تعلیم دیده بود، رویکرد هندسی اقلیدس را ادامه داد، ولی آن را به قلمرو بسیار دشوارتری کشاند. برای مثال، او در کتابش بنام ”در باب مخروط‌ها و کره‌گون‌ها“، مقاط مخروطی را مطالعه می‌کند. بر این اساس، روشن است که ارشمیدس می‌توانسته انواع خاصی از معادلات درجه سوم را حل کند. این درست مانند این بود که اقلیدس توانسته بود برخی از انواع معادلات درجه دوم را حل کند، ولی همه اینها به زبان هندسه بودند.

ارشمیدس (212-287 ق.م).

2.4

پس از دوران شکوه خودش در قرن سوم پیش از میلاد، ریاضیاتِ اسکندریه دچار افول شد، و در قرن یکم پیش از میلاد که بی‌نظمی حکم‌فرما بود (مقارن با زمانی که آنتونی و کلئوپاترا زندگی می‌کردند)، بنظر می‌رسد که کلاً پژمرده شده بود.

شکل 1-2: نمایی از شهر اسکندریه باستان.

در ابتدای دروران تسلط رومی‌ها بر مصر، ریاضیات اسکندریه دوباره احیاء شد. همچنین یک تغییر فکری نیز در آنجا پدید آمد، و باعث شد آنها از رویکردهای کاملاً هندسی کمی فاصله بگیرند. و در همین دوره بود که دیافانتوس بدنیا آمد و کار کرد.

دیافانتوس

همانطور که در ابتدای این فصل بطور تلویحی بیان کردم، ما تقریباً هیچ چیز از زندگی دیافانتوس، و حتی اینکه او در چه قرنی می‌زیسته، نمی‌دانیم. بهترین حدسی که در اینمورد زده می‌شود، قرن سوم میلادی است، میان سال‌های 200 تا 284. ما دیافانتوس را از روی رساله‌ او بنام حساب (Arithmetica) می‌شناسیم، که تقریباً نیمی از آن بجا مانده. بخش اعظم رساله بجا مانده حاوی 189 مسئله است که هدف آنها یافتن اعداد، یا دسته‌ای از اعداد است که در شرایط خاصی صدق کنند. در شروع این رساله مقدمه‌ای ذکر شده که در آن دیافانتوس رئوس نمادگذاری‌های خودش را ذکر می‌کند.

امروزه ممکن است نماگذاری دیافانتوس ابتدایی بنظر برسد، ولی در زمان خودش بسیار پیچیده بود. این را می‌توانم با یک مثال نشان دهم. در زیر معادله‌ای را می‌بینید که به شکل امروزی نوشته شده:

و دیافانتوس همین معادله را به صورت زیر می‌نویسد:

آسان‌ترین چیزی که در اینجا می‌توان آن را دید اعداد هستند. دیافانتوس از حروف الفبای یونانی برای نوشتن اعداد استفاده می‌کرد. اینکار با استفاده از 24 حرف الفبای یونانی، به همراه سه حرف دیگری که اکنون منسوخ شده‌اند انجام می‌گرفت. تمام این 27 حرف به سه گروه نُه‌تایی تقسیم بندی می‌شدند. اولین گروه، ارقام میان 1 تا 9 را نمایش می‌دادند؛ دومین گروه، دهگان‌ها از 10 تا 90 را نشان می‌دادند؛ و سومین گروه، صدگان‌ها را از 100 تا 900 نشان می‌دادند. یونانی‌ها هیچ علامتی برای نشان دادن صفر نداشتند؛ البته در آن زمان هیچ کس دیگری هم برای صفر علامتی نداشت.

بنابراین در معادله‌ای که نشان دادم، نشان دهنده 1، نشان دهنده 2، نشان دهنده 10، و نشان دهنده 5 است. (خطوطی که در بالای هر حرف آمده نمایانگر این است که این حروف نشاندهنده اعداد هستند.)

علامت‌های دیگری مثل ίσ مخفف ίσος به معنای ”مساوی“ هستند. توجه کنید که هیچ خطی در بالای این حروف قرار ندارد؛ این علامت‌ها هیچ عددی را نشان نمی‌دهند، و تنها نماینده حروف یک لغت هستند (که معمولاً بصورت مخفف نمایش داده می‌شوند). حرف چنگک وارونه (Ψ) به معنی تفریق هر آنچه بعد از آن تا رسیدن به علامت ”مساوی“ است.

حالا می‌ماند چهار علامت دیگر: K^Y، ς، ^Y∆، و M. علامت ς نشان‌دهنده کمیت مجهول است، که امروزه آن را بصورت x نشان می‌دهیم. بقیه نشان دهنده توان‌های کمیت مجهول هستند: K^Y یعنی توان سوم (که از لغت یونانی κύβος، به معنی مکعب گرفته شده)، ^Y∆ یعنی توان دوم، و M یعنی توان صفرام، که امروزه به نام ”جمله ثابت“ شناخته می‌شود.

حال که با این موارد آشنا شدیم، می‌توانیم جزء به جزء معادله دیافانتوس را به شکل امروزی ترجمه کنیم:

اگر از علامت بعلاوه (+) و پرانتز استفاده کنید، عبارت بالا قابل‌فهم‌تر خواهد بود:

به دلیل اینکه دیافانتوس بجای اینکه ضرایب را قبل از مجهول قرار دهد آن را بعد از مجهول قرار می‌داد (یعنی بجای اینکه بنویسد 10x، می‌نوشت x10)، و بدلیل اینکه هر عددی که بتوان صفر برسد حاصل آن 1 خواهد بود، معادله فوق با معادله زیر، یعنی همان معادله اولیه من یکسان خواهد بود:

از این مثال می‌توان فهمید که دیافانتوس نوعی نمادگذاری جبری پیچیده را در اختیار داشته. معلوم نیست که چه مقدار از این نمادگذاری‌ها در اصل به خود او تعلق داشته. استفاده از نماد‌های خاص برای مربع و مکعبِ مجهول احتمالاً ابداع خود دیافانتوس بوده. ولی بنظر می‌رسد استفاده از علامت ς برای کمیت مجهول، به نویسنده قدیمی‌تری تعلق داشته باشد، که پاپیروسی را نوشته که به پاپیروس 620 میشیگان معروف است و در دانشگاه میشیگان نگاهداری می‌شود.

البته دستگاه نمادگذاری دیافانتوس کمبودهایی نیز دارد. عمده‌ترین کمبود آن این است که نمی‌تواند بیش از یک مجهول را نمایش دهد. به عبارت امروزی، این دستگاه می‌تواند مجهولی مثل x را نمایش دهد، ولی نه بیشتر (مثلاً y و z). این برای دستگاه دیافانتوس نقیصه عمده‌ای است، زیرا بیشتر کتاب او با معادلات سیاله سر و کار دارد. این مورد جای توضیح دارد.

2.5

آنطور که ریاضیدانان از لغت ”معادله“ (equation) استفاده می‌کنند، معادله به معنای عبارتی است که در آن چیزی با چیز دیگری مساوی است. اگر من بگویم ”دو دوتا مساوی چهار است“، من یک معادله را بیان کرده‌ام. البته معادلاتی که ریاضیدانان، از جمله دیافانتوس، به آن علاقه دارند، آنهایی هستند که در آن یک سری کمیت‌های مجهول حضور دارد. حضور یک مجهول در یک معادله، آن را از حالت ”خَبری“ به حالت ”پرسشی“ تبدیل می‌کند. مثلاً معادله

x+2=4

به سادگی این سئوال را می‌پرسد که ”چه عددی بعلاوه دو مساوی چهار است؟“ که البته جواب آن 2 است. این معادله وقتی برقرار است که x=2 باشد.

ولی فرض کنید من سئوال زیر را بپرسم:

x+y+2=4

جواب این سئوال چیست؟ حالا ما به آب‌های عمیقتری وارد می‌شویم.

در وهله نخست یک ریاضیدان فوراً می‌خواهد ببیند که شما به دنبال چه نوع جواب‌هایی هستید. آیا اعداد صحیحِ مثبت مورد نظر شماست؟ در این صورت تنها جواب این معادله x=1, y=1 است. آیا می‌خواهید جواب‌های شما شامل صفر هم بشود؟ در این صورت این معادله جواب‌های بیشتری را خواهد داشت: (اولی) x=0, y=2، و (دومی) x=2, y=0. آیا اعداد منفی هم می‌توانند در جواب‌های شما ظاهر شوند؟ در این صورت حالا معادله شما بی‌نهایت جواب خواهد داشت. آیا اعداد کسری را هم مجاز می‌دانید؟ در این صورت نیز معادله شما بی‌نهایت جواب خواهد داشت: کسرهایی مثل ... و غیره. و البته اگر اعداد گنگ و مختلط را نیز مجاز می‌دانید، در این صورت محدوده گسترده‌تری از بی‌نهایت جواب را خواهید داشت.

معادله‌هایی از این دست، که بیشتر از یک مجهول دارند، و بسته به نوع جواب‌ها، بطور بالقوه می‌توانند بی‌نهایت جواب‌ داشته باشند، معادلات نامعین یا سیاله (indeterminate) نام دارند.

معروف‌ترین معادله سیاله همان است که در آخرین قضیه فرما مطرح می‌شود و بصورت زیر است:

xⁿ+yⁿ=zⁿ

که در آن x,y,z و n همگی باید اعداد صحیح مثبت باشند. اگر n=1 یا n=2 باشد، این معادله دارای بی‌نهایت جواب است. آخرین قضیه فرما می‌گوید اگر n>2 باشد، این معادله هیچ جوابی ندارد.

پی‌یر دو فِرما (1665-1607)

هنگامی که در حوالی سال‌های 1637 این قضیه به پی‌یر دو فِرما (Pierre de Fermat) الهام شد، او مشغول خواندن ترجمه لاتینی کتاب حساب دیافانتوس بود، و یادداشتی که فرما بر حاشیه این کتاب نوشت، او را تا ابد مشهور ساخت. او در این یادداشت قضیه خودش را مطرح کرده و اضافه می‌کند: ”من یک اثبات بسیار عالی برای این قضیه یافته‌ام، ولی کوچک بودن حاشیه کتاب اجازه نمی‌دهد آن را در اینجا بنویسم.“ 357 سال بعد، این قضیه توسط ریاضیدان انگلیسی اندرو وایلز (Andrew Wiles) اثبات شد.

اندرو وایلز (-1953)، زمانی که اثبات خودش برای آخرین قضیه فرما را ارائه داد (1994).

2.6

همانطور که گفتم، کتاب حساب دیافانتوس حاوی معادلات سیاله است، و همانطور که باز هم اشاره کردم، این نمادگذاری دیافانتوس را در تنگنای شدیدی قرار می‌دهد، زیرا او تنها می‌توانست از یک نماد برای مجهول خودش استفاده کند (از نمادهای دیگر برای نشان دادن مربع، مکعب، و غیره استفاده می‌کرد).

برای اینکه ببینیم او چگونه با این مشکل برخورد می‌کرد، در اینجا به مثالی می‌پردازم که فرما در حاشیه کتاب خودش برای مسئله شماره 8 جلد دوم نوشته بود.

دیافانتوس مسئله‌ای را به این صورت مطرح می‌کند: ”یک عدد مربع داریم که باید آن را به صورت حاصل جمع دو عددِ مربع دیگر نشان دهیم.“ ما امروزه می‌دانیم که این مسئله را می‌توانیم به این صورت بیان کنیم: ”عدد مفروضی مانند a داریم، اعدادی مانند x,y را پیدا کنید که رابطه x²+y²=a² برقرار باشد.“ البته دیافانتوس نمادگذاری پیچیده‌ای مانند آنچه ما حالا داریم نداشت، بنابراین او مسئله را بشکل لفظی بیان می‌کرد.

برای حل این مسئله، او برای a مقدار مشخصی، مثل 4، تعیین می‌کرد. بنابراین ما بدنبال مقادیری برای x,y هستیم که در آن x²+y²=16. سپس او y را بصورت عبارتی از x می‌نوشت، که گویا چنین عبارتی اختیاری بود، مثلاً می‌گفت y=2x-4. بنابراین ما معادله خاصی برای حل کردن داریم که تنها یک مجهول دارد:

x²+(2x-4)²=16

معادله فوق یک معادله درجه دوم ساده است، و دیافانتوس می‌دانست که چگونه آن را حل کند. جواب آن است (البته جواب دیگری هم دارد که x=0 است، ولی دیافانتوس هیچ راهی برای نمایش صفر نداشت، بنابراین این جواب را نادیده می‌گرفت). پس ما خواهیم داشت .

چنین جواب‌هایی خیلی گیرا نیستند، و در واقع شبیه تقلب هستند. معادله x²+y²=a² دارای بی‌نهایت جواب است، که دیافانتوس تنها یکی از آنها را بدست آورده. او برای این کار از رویه‌ای استفاده کرده بود که به سادگی می‌توان آن را تعمیم داد، و او از این حقیقت آگاه بود که برای این مسئله، تعداد بی‌نهایتی از جواب‌های دیگر نیز وجود دارند (او در جای دیگری از کتابش به این موضوع اشاره می‌کند).

2.7

قبلاً اشاره کردم وقتی که یک ریاضیدان با یک معادله سیاله مانند x+y+2=4 روبرو می‌شود، این سئوال را مطرح می‌کند که ”شما به دنبال چه نوع جواب‌هایی برای این معادله هستید؟“ در مورد معادله دیوفانتی که قبلاً مثال زدم، آنچه مورد نظر بود اعداد مثبتِ گویا، نظیر و بودند. اعداد منفی و صفر نیز هنوز اختراع نشده بودند. از نظر دیوفانتوس، معادله‌ای نظیر 4x+20=4 ”بی‌معنی“ بنظر می‌رسید. البته او با اعداد گنگ آشنا بود، ولی علاقه‌ای به آنها نداشت. هنگامی که سرو کله این اعداد در یک مسئله پیدا می‌شد، او طوری جملات معادله را تنظیم می‌کرد که فقط جواب‌های گویا را بگیرد.

جستجو برای جواب‌هایی که بصورت اعداد-گویا باشند، مانند همان معادلاتی که دیافانتوس حل می‌کرد، در واقع معادل یافتن جواب‌های صحیح معادله است. مثلاً معادله

در واقع معادل عبارت زیر است:

16²+12²=20²

بنابراین امروزه ”آنالیز دیوفانتی“ به معنای ”یافتن جواب‌های صحیح برای معادلات چندجمله‌ای“ است.

2.8

خواننده این کتاب احتمالاً هنوز از روش دیافانتوس برای حل x²+y²=a² تحت تاثیر قرار نگرفته. اگر بخواهیم در مورد دیافانتوس انصاف را رعایت کنیم، باید بگویم گرچه مطرح کردن مسئلهِ فوق ساده است، ولی او مسائل سخت‌تری را نیز حل کرد. معادله x²+y²=a² روش او را بخوبی نشان می‌داد. این ارتباط جالبی با آخرین قضیه فرما دارد و توضیح آن راحت است، و به همین خاطر، مثالِ معروفی است. در جاهای دیگر دیافانتوس به معادلات درجه سوم و چهارم می‌پردازد که تنها یک مجهول دارند. در جاهای دیگر به دستگاه معادلات همزمان می‌پردازد که دارای دو، سه، و چهار مجهول هستند. او همچنین مسئله‌ای را مطرح می‌کند که شامل دستگاهی از 8 معادله و 12 مجهول است.

دیافانتوس از آنچه برای حل معادله x²+y²=a² انجام داده بود بیشتر می‌دانست. او از قواعد مربوط به علامت‌ها آگاهی داشت، و آنها را بیان کرد:

حاصل ضرب کمبود (یعنی منفی) در کمبود می‌شود موجود (یعنی مثبت). حاصل ضرب کمبود در موجود می‌شود کمبود.

با توجه به اینکه قبلاً اشاره کردم در زمان دیافانتوس اعداد منفی هنوز کشف نشده بودند، این چیز قابل ملاحظه‌ای است.

در واقع آنچه به عنوان ”کشف نشده“ از آن یاد کردم نیاز به کمی تعدیل دارد. گرچه دیافانتوس هیچ نمادی برای اعداد منفی بعنوان اشیاء مستقل ریاضی نداشت و آنها را بعنوان جواب معادلات بحساب نمی‌آورد، ولی او در درون محاسبات خودش از آنها آزادانه استفاده می‌کرد. مثلاً اگر 2x+7 را از x²+4x+1 کم کنیم، حاصل x²+2x-6 خواهد بود. گرچه او -6 را بطور وضوح بعنوان یک شیء ریاضی ”بی‌معنی“ می‌دید، ولی اگر لازم بود، او قبول داشت که 1-7 برابر -6 است.

مواردی مانند این موجب می‌شود ما تصور کنیم که تفکرِ ریاضی چقدر غیرطبیعی است. حتی درمورد مفاهیم ساده‌ای مثل اعداد منفی نیز قرن‌ها طول کشید تا آنها در ذهن ریاضیدانان روشن شوند. این ”روشن شدن“ بتدریج انجام گرفت و شامل یک سری مراحلِ هشیاری نظیر آنچه مثال زدم بود. 1300 سال بعد از دیافانتوس، چیزی مشابهی در مورد اعداد موهومی اتفاق افتاد.

دیافانتوس همچنین می‌دانست چگونه با تغییر علامتِ جملات می‌تواند آنها را از یک طرف معادله به طرف دیگر منتقل کند، یا برای ساده کردن عبارات، چگونه جملات مشابه را با هم جمع کند، و از اصول ابتدایی بسط و فاکتورگیری نیز آگاه بود.

بعدها در زمان ما، تلاش دیافانتوس برای یافتن جوابهای گویا، انگیزه نظریه اعداد جبری شد. حالا ما می‌گوییم معادله x²+y²=a²معادله دایره‌ای به شعاع a است. برای بدست آوردن جواب‌های گویای این معادله، ما می‌پرسیم چه نقاطی روی یک دایره به شعاع a قرار دارند که مختصات x,y آنها اعدادی گویا هستند؟ همانطور که در بخش 14.4 خواهید دید، قطعاً این یک سئوال امروزی است.

2.9

پس آیا دیافانتوس پدر جبر بود یا نه؟ من مایلم بخاطر استفاده از نمادهای لفظی که او از آنها استفاده می‌کرد، چنین اعتباری را به وی بدهم. اولین باری که من یکی از معادلات او را دیدم که با نمادگذاری وی نوشته شده بود، مانند خیلی‌ها، واکنش من نیز این بود که ”او چه می‌گوید؟“ ولی بعداً وقتی با مسائلی که او مطرح کرده بود آشنا شدم و توانستم تا حدی آنها را بخوانم، این معادلات برایم مانوس‌تر شدند.

حداقل توانستم ارزش کار او را درمورد نمادگذاری‌هایش و پیشرفت بزرگی که او بانی آن بود را درک کنم. وگِل درباره درباره کتاب حسابِ دیافانتوس گفته بود ”این کتاب فاقد روش‌های کلی است“، و من این نکته را قبول دارم، و همچنین قبول دارم که موضوعاتی که او انتخاب کرده اصیل نبوده‌اند، و او احتمالاً اولین کسی نبوده که از یک علامت خاص برای کمیت مجهول استفاده کرده.

ولی از بختِ خوشِ تاریخ، دیافانتوس از اولین کسانی بود که چنین مسائلِ جامع و متنوعی را گردآوری کرد و آنها را برای ما به یادگار گذاشت. مایه شرمساری است که ما دقیقاً نمی‌دانیم اولین نفری که از یک علامت برای نمایش یک کمیت مجهول استفاده کرد چه کسی بوده، ولی بدلیل اینکه دیافانتوس بخوبی و خیلی زود از آن استفاده کرده بود، ما باید این اعتبار را به وی بدهیم. احتمالاً کسی که ما نمی‌شناسیم، و هیچ وقت هم نخواهیم شناخت، پدر واقعی جبر بود. ولی بدلیل اینکه جای این عنوان خالیست، ما می‌توانیم آن را با باارزش‌ترین نامی که از دنیای باستان می‌شناسیم پر کنیم، و این نام دیافانتوس است.

شکل 2.2: فانوس دریایی اسکندریه، از نظر نقاش آن مارتین هیمسکرک (Martin Heemskerck) (1574-1498).

فصل 3

تکمیل و احیا

22/04/1401

3.1

همانطور که همه می‌دانند لغت ”جبر“ (al-gebra) از زبان عربی آمده. بنا به دلایلی که به زودی بیان خواهم کرد، از نظر من چنین چیزی کمی غیرمنصفانه است. چه منصفانه باشد چه نباشد، این موضوع از لحاظ تاریخی نیاز به توضیح دارد.

3.2

اگر آن تاریخی که من برای دیافانتوس ذکر کردم (284-200 میلادی) درست باشد، باید بگویم او در دوران بسیار ناگواری زندگی می‌کرد. امپراتوری روم، که مصر هم یکی از ایالات آن بود، قدم به سقوط و انحطاط گذاشته بود. اگر او حقیقتاً در این زمان زندگی می‌کرده، این همان دورانی است که در فصل هفتم کتابِ بی‌نظیر ”تاریخ انحطاط امپراتوری روم“، نوشته ادوارد گیبون، بخوبی شرح داده شده.

بعداً این امپراتوری در قرن سوم دوباره کمی سر و سامان گرفت. در آن دوران، کسانی مانند دیوکلتیان (Diocletian) و کنستانتین (Constantine) ظهور کردند که از امپراطوران بزرگ روم محسوب می‌شدند. دیوکلتیان کسی بود که با بی‌رحمی بدنبال آزار مسیحیان بود، و کنستانتین فرزند یک مسیحی بود که با صدور فرمانی که به به حکمِ میلان معروف است (سال 313)، فرمان داد که در سراسر امپراطوری با مسیحیان با مدارا رفتار شود، و خود او هم در سال‌های آخر بیماری خودش قبول کرد که غسل تعمید داده شود.

این که ابتدا با مسیحیان مدارا شود، و بعد به زور مسحیت بر مردم تحمیل شود، تاثیر اندکی بر سقوط امپراطوری داشت. از برخی جهات، حتی ممکن است این کارها موجب تسریع سقوط امپراطوری نیز شده باشد. یکی از نقاط قوت مسیحیتِ اولیه، موضوع برابری همه طبقات بود. ولی برای اعمال چنین هدفی باید به نظریه‌های پیچیده متافیزیکی توسل می‌جستند. ولی توده مردم هنگامی که با بادهای پرغرور بحث‌های متافیزیکی روبرو شدند، از آنها بعنوان سلاحی برای ابراز نارضایتی‌های نژادی استفاده کردند.

شهر خودِ دیافانتوس، یعنی اسکندریه، این روند را بخوبی نشان می‌دهد. اسکندریه حتی بعد از گذشت 300 سال بعنوان یک شهر یونانی، و نیز 300 سال دیگر بعنوان یک شهر رومی، باز هم یک ناحیه شهری ممتاز باقی‌مانده بود که از لحاظ غذا و لباس به روستاییان بی‌سواد نواحی اطراف که به زبان قبطی صحبت می‌کردند وابسته بود. از دید یک مسیحیِ قبطی که در نواحی حاشیه‌ای مصر زندگی می‌کرد، لغات ”یونانی“، ”رومی“، و ”کافر“ تقریباً به یک معنا بودند. همچنین معبد شگفت‌انگیز موزها (Museion) با آن کتابخانه بزرگ، و سُنت دیرینش در آموزش‌های سِکولار، از نظر قبطی‌ها همچون خانه شیطان بود.

این موضوع هنگامی در مصر بدتر شد که فرقه‌ای از دیرنشینان، که شامل مردان جوانی می‌شدند که به شدت از لحاظ جنسی گرسنه بوند، به خدمت روحانیان مسیحی درآمدند که می‌خواستند کافران و ناباوران را شلاق بزنند. همین بود که در سال 415 میلادی زمینه قتل هیپاتیا (Hypatia) را فراهم آورد، و موجب انزجار ادوارد گیبون، تاریخ‌نگار معروف شده بود.

هیپاتیا اولین زنی است که نامش در تاریخ ریاضیات مطرح می‌‌شود. کلیه آثار او گم‌شده‌اند، و آنچه ما از او می‌دانیم تنها از طریق شایعاتی است که درباره او وجود دارد. بر این اساس، واقعاً مشکل است قضاوت کرد که آیا می‌توان او را یک ریاضیدان برجسته بحساب آورد یا نه. ولی به هر صورت مطمئناً او یک چهره مهم و روشنفکر بوده. او در مدرسه موزها، که پدرش تئون آخرین مدیر آنجا بود، آموزش دید، و مسئول جمع‌آوری، ویرایش، و حفظ متون، از جمله متون ریاضی بود. او معلم فلسفه بود، و پرو مکتبی بود که نوافلاطونی (Neoplatonism) نامیده می‌شود. این فلسفه تلاش می‌کرد در جهانِ دیگری بدنبال نظم، عدالت، و صلح باشد، چیزهایی که در امپراطوری روم بطور آشکار فقدان آنها حس می‌شد. او همچنین یک زن زیبا و باکره بود.

در زمانی که سیریل اسکندرانی (Cyril of Alexandria) اسقفِ شهر اسکندریه بود، هیپاتیا در آموزش و پرورش فعال بود. بدلیل ابرهای تیره تاریخ، و جدال‌های مذهبی، مشکل می‌توان درباره سیریل، که بعدها به ”سیریلِ مقدس“ معروف شد، قضاوت کرد. مطمئناً این سیریل بود که یهودیان اسکندریه را قتل‌عام کرد، و آنها را از شهر فراری داد، ولی بنظر می‌رسد که پیش از آن، این خود یهودهای بودند که دست به کشتار مسیحیان زده بودند. آنگونه که در دائره‌المعارف کاتولیک نوشته شده، در آن زمان اسکندریه همیشه پرآشوب بود. به هرصورت، سیریل بر سر حاکمیت کلیسا با حاکم رومی مصر، ارستیز، در حال نزاع بود، و بدروغ به او گفته شده بود که هیپاتیا یک مانع عمده برای توافق است. پس از آن عده‌ای جمع شدند و هیپاتیا را از ارابه‌اش پایین کشیدند و او را روی زمینی که با خورده‌های کوزه، یا صدف‌های شکسته، پوشانده شده بود کشاندند، طوری که گوشت از استخوانش جدا شد.

تصویری از هیپاتیا و به زمین کشاندن آن به دست متعصبان مسیحی.

بنظر می‌رسد که هیپاتیا تا زمان مرگش، یعنی سال 415 میلادی، آخرین کسی باشد که در مدرسه موزها تدریس می‌کرد. از این زمان بعنوان پایان ریاضیات در اروپای باستان یاد می‌شود. امپراطوری روم 60 سال دیگر در غرب به حیات خود ادامه داد. اسکندریه نیز به مدت 164 سال تحت حاکمیت امپراطوری بیزانس به حیات خود ادامه داد (به غیر از وقفه کوتاهی که میان سال‌های 629-616 به جهت حمله مسلمانان به آنجا پیش آمد)، ولی حیات روشنفکری از آنجا رخت بر بسته بود. شخصیت بعدی که در تاریخ جبر اهمیت دارد، 1500 کیلومتر با اسکندریه فاصله داشت، و پانصد سال بعد در کرانه‌های رود دجله زندگی می‌کرد.

3.3

در قرن پنجم میلادی، نواحی شمالی و غربی امپراطوری روم به دست اقوام غیر-مسیحی ژرمن افتاد. در قرن هفتم، قسمت‌های جنوبی، و شرقی (به غیر از یونان، آناتولی، و برخی از نواحی جنوبی ایتالیا و بالکان) به دست مسلمانان افتاد. در زمان هراکلیوس که امپراطور بیزانس بود و تمامی عمرش را صرف این کرده بود که سرزمین‌های از دست رفته را از دست مسلمانان خارج کند، خود اسکندریه در 23 فوریه 640 به دست مسلمانان سقوط کرد.

فاتح اصلی اسکندریه شخصی بود بنام عمروعاص. او تحت فرمان مستقیم خلیفه دوم مسلمانان، یعنی عُمر بود. در حالی که بقیه مصر تحت کنترل مسلمانان درآمده بود، اسکندریه برای مدت 14 ماه در محاصره بود.

خلیفه سوم مسلمانان، یعنی عثمان، که از خاندان بنی‌امیه بود، بعد از یک سری جنگ‌های داخلی که با خلیفه چهارم، علی‌ابن ابی‌طالب داشت (و بعدها به ایجاد دو فرقه سنی و شیعه امروزی در اسلام منجر شد)، خاندان بنی‌امیه را تاسیس کرد که برای مدت 90 سال، در شهر دمشق از 661 تا 750 میلادی بر جهان اسلام حکومت کرد. شورشی که بوجود آمد منجر به تغییر خاندان شد، و بنی‌امیه تنها اسپانیا را حفظ کرد، که برای 300 سال تحت سطله مسلمانان باقی ماند.

نسبت این خاندان جدید به عموی پیامبر اسلام، یعنی عباس می‌رسید، بنابراین آنها بنام عباسیان در تاریخ شناخته می‌شوند. آنها در سال 762 برای فراهم آوردن مصالح ساختمانی و تاسیس پایتخت جدید خودشان، بغداد، ایران و بابِل را غارت کردند. لغت عربی ”جبر“ از عنوان کتابی گرفته شده که در حدود سالهای 820 توسط ابوجعفر محمدابن موسی الخوارزمی نوشته شده. مانند بسیاری از کتاب‌های دیگر، من نیز در این کتاب از او بعنوان خوارزمی یاد خواهم کرد.

3.4

تحت حکمرانی خلفای پنجم، ششم، و هفتم عباسی (میان سالهای 786 تا 833 میلادی)، بغداد یک مرکز مهم فرهنگی بود، همان جایی که در نظر مردمان امروزی غرب یادآور لغاتِ وزیر، برده، کاروان، و سفرهای دور و درازی است که در داستان‌های هزار و یک شب از آنها یاد شده (سندباد و علی بابا). گرچه این خلفا آنقدر قوای نظامی نداشتند تا فتوحاتی که در صدر اسلام انجام گرفته بود را حفظ کنند و کم‌کم این سرزمین‌ها را در شمال آفریقا و قفقاز از دست می‌دادند، ولی خود اعراب از این دوره به عنوان دوران طلایی نام می‌برند.

ایران بخشی از قلمرو عباسیان بود که تحت حاکمیت دینی خلیفه قرار داشت. درحالی که در سال 800 میلادی، تنها چند نسل بود که اعراب از بادیه‌نشینی خارج شده بودند، ایران از 1400 سال پیش از این، یعنی از زمان مادها، دارای یک تمدن بسیار پیشرفته بود. بنابراین عباسیان نسبت ایرانیان نوعی حقارت فرهنگی را حس می‌کردند، درست مانند رومی‌ها نسبت به یونانیان.

فراسوی ایران هند قرار داشت، که از گسترش اولیه اسلام دست نخورده باقی مانده بود. شمال هند در قرون چهارم و پنجم میلادی تحت حکمرانی سلسله گوپتا بود، ولی بعد از فتوحاتی که سلجوقیان در قرن دهم در آن نواحی به عمل آوردند، هند به بخش‌های مختلفی تقسیم شد. این تمدن‌های قرون وسطایی هندی مجذوب اعداد بودند، علی‌الخصوص اعدادِ بزرگ، و برای آنها اسامی مختلفی را انتخاب کرده بودند (مثلاً اگر به لغت هندی تالاکچانا برخورد کردید، به معنی صد هزار تریلیون تریلیون تریلیون تریلیون است). این ریاضیدانان هندی‌ بودند (احتمالاً براهماگوپتا در حوالی سال‌های 598 تا 670 میلادی) که افتخار ابدی کشف عدد صفر و عدد نویسی امروزی، که سیستم هندی-عربی نامیده می‌شود، به آنها تعلق دارد.

البته فراسوی هندوستان سرزمین چین قرار داشت، که حداقل برای چندین قرن قبل از میلاد، میان آنها و هندیان داد و ستد تجاری و فرهنگی برقرار بود، و ایرانیان برای این داد و ستدها جاده شلوغ راه ابریشم را ایجاد کردند. چینی‌ها خودشان یک فرهنگ طولانی ریاضی داشتند، که من بعداً در بخش 9.1 درباره آن بیشتر توضیح خواهم داد.

بنابراین، مسلمانانی که می‌خواستند از آنچه در جهان متمدن آن زمان می‌گذرد آگاهی پیدا کنند، می‌توانستند اینکار را انجام دهند. فرهنگ و تمدن یونانی و رومی از طریق اسکندریه (که حالا جزیی از قلمرو آنها بود) و همچنین از طریق تماس‌های بازرگانی با امپراطوری بی‌زانس، در دسترس آنها قرار داشت. فرهنگ‌های ایرانی، هندی، و چینی نیز به آسانی در دسترس آنها بود.

آنچه نیاز بود بغداد را به مکان مطلوبی برای حفظ و غنای دانش آن زمان تبدیل کند، تاسیس یک آکادمی بود، مکانی برای رجوع به اسناد و درس‌هایی که دانش‌پژوهان می‌توانستند به آنها رجوع کنند. چنین آکادمی بزودی تاسیس شد، و دارالحکمه، یا ”خانه دانش“ نام گرفت. اوج شکوفایی این آکادمی در زمان مامون، خلیفه هفتم بود. به قول سِر هنری راولینسون، بغدادِ زمانِ مامون، یا شهر قرطبه (کوردوا) از لحاظ ادبیات، هنر، و دانش از همه شهرهای جهان بالاتر بودند. در همین زمان بود که خوارزمی زندگی می‌کرد.

3.5

ما در مورد زندگی خوارزمی چیز زیادی نمی‌دانیم. تاریخ‌های مربوط به او تقریبی هستند. تنها چیزی که می‌دانیم این است که او چند کتاب نوشته بود: یکی در مورد نجوم، یکی درباره جغرافی، یکی درمورد تقویم یهودی، یکی درمورد عدد نویسی هندی، و یکی هم درباره وقایع‌نگاری تاریخی.

کتاب او درباره عدد نویسی هندی تنها از طریق ترجمه لاتین آن بجا مانده، که با این لغات شروع می‌شوند ”دیکسی الگوریتمی ...“. این کتاب قواعد محاسبه با اعداد 10 رقمی امروزی را مشخص می‌کند، یعنی همان چیزی که هندی‌ها آن را اختراع کردند، و بعداً بسیار تاثیر گذار و فراگیر شد. بدلیل لغاتِ آغازین این کتاب، دانشوران اروپایی که در این نوع محاسبه استاد شدند (در مقایسه با دستگاه عدد نویسی رومی، که کلاً اصلاح‌ناپذیر بود)، به خودشان ”الگوریتمیست“ (algorithmists) می‌گفتند. ریشه لغت الگوریتم (algorithm) که حالا ما خیلی از آن استفاده می‌کنیم نیز همین است. معنی امروزی این لغت در ریاضیات و علوم رایانه‌ای این است: هر روند محاسباتی که بخوبی تعریف شده باشد و طی یک سری مراحل متناهی انجام گیرد.

ابوموسی خوارزمی

کتابی که در اینجا مورد نظر ما است ”الکتاب المختصر فی حساب الجبر و المقابله“ نام دارد، که یعنی راهنمای محاسبه به روش تکمیل و تقلیل است. این کتاب به جبر و حساب مربوط است، که پس از 600 سال بعد از دیافانتوس، اولین اثر مهم در این حوزه محسوب می‌شود. این کتاب به سه بخش تقسیم می‌شود و سه موضوع را دنبال می‌کند: حل معادلات درجه دوم، اندازه‌گیری مساحت‌ها و حجم‌ها، و ریاضیاتِ مربوط به قوانین پیچیده ارث در اسلام.

تنها بخش اول این کتاب بصورت کامل به جبر مربوط است، و این ناامید کننده است. در کتاب خوارزمی هیچ نمادگذاری به چشم نمی‌خورد، یعنی از حروف الفبا و اعداد، و همچنین از علامت مثبت و منفی برای نوشتن مجهولات و معادلات استفاده نمی‌کرد. معادله‌ای که ما امروزه آن را بصورت زیر می‌نویسم

x²+10x=39

و یا دیافانتوس آن را بصورت زیر می‌نوشت

∆^Yα ςι σM λθ

در کتاب خوارزمی به شکل زیر بیان می‌شود:

یک مربع و ده ریشه همان کمیت، با 39 دِرهم مساوی است؛ این یعنی، چه چیزی است که اگر آن را مربع کنیم و آن را با ده برابر خودش جمع کنیم، حاصل 39 خواهد بود؟

(در آن زمان، دِرهم واحد پول بود، و خوارزمی از آن برای رجوع به چیزی استفاده می‌کرد که امروزه جمله ثابت (یا x⁰) نامیده می‌شود.)

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

موضوعات ریاضی

معادلات درجه سوم و چهارم

/01/05/1401

1

پس از قرون وسطی، اولین پیشرفت بزرگی که در جبر اتفاق افتاد حل معادلات درجه سوم، و بلافاصله بعد از آن معادلات درجه چهارم بود، که من جزئیات آن را در فصل بعدی بیان خواهم کرد. ولی ابتدا می‌خواهم از نظر ریاضیدانان قرن شانزدهم نگاهی به این موضوع بی‌اندازیم. در اینجا برای روشن شدن موضوع و مشکلات آن، من فقط بطور مختصر جبر مربوط به آن را توضیح خواهم داد.

مهم است بدانیم آنچه که مورد نظر بوده چیست. حل تقریبی معادلات درجه سوم، یا حتی معادلاتی با درجات بالاتر، و بدست آوردن جواب‌های عددی برای آنها که دقت بالایی نیز داشته باشند، زیاد سخت نیست. برخی اوقات شما می‌توانید جواب درست یک معادله را حدس بزنید. رسم نمودار شما را به گرفتن جواب خیلی نزدیک می‌کند. برای بدست آوردن چنین جواب‌هایی قبلاً یونانیان، اعراب، و چینی‌ها روش‌های پیچیده‌ حسابی و هندسی را ابداع کرده بودند. ریاضیدانان اروپایی قرون وسطی با این روش‌ها آشنا بودند و می‌توانستند با تقریب‌های خوبی جواب‌های عددی یک معادله درجه سوم را بدست آورند.

چیزی که آنها در دست نداشتند، یک حلِ کُلیِ جبری برای این معادلات بود (یعنی یک فرمول کلی که بتوانند از آن برای حل معادلات درجه سوم استفاده کنند، درست مانند فرمول معروف که از آن برای حل معادله ax²+bx+c=0 استفاده می‌شود). یک فرمول عمومی چیزی بود که ریاضیدان آن عصر بدنبال آن بودند. تنها زمانی معادلات درجه سوم یک مسئله حل شده تلقی می‌شدند که چنین فرمولی برای آنها یافت می‌شد.

2

شکل کلی یک معادله درجه سوم تک مجهوله به این صورت است:

x³+Px²+Qx+R=0

اولین کاری که ما می‌خواهیم انجام دهیم، حذف جمله x² از این معادله است، که این کار توسط رابطه جبری ساده زیر صورت می‌گیرد:

که می‌شود آن را بصورت معادله دیگری بیان کرد:

که در اینجا X=x+P/3 است. بنابراین با یک جانشینی ساده، هر معادله درجه سوم را می‌توان طوری بازنویسی کرد که جمله x² نداشته باشد، و اگر بتوانیم با یافتن مقداری برای X معادله دوم را حل کنیم، به سادگی با کم کردن P/3 از آن می‌توانیم مقدار x را نیز پیدا کنیم. این نوع از معادلات درجه سوم، که جمله x² در آن وجود ندارد، معادلات درجه سوم تنزل یافته (depressed) نامیده می‌شود، که شکل کلی آنها بصورت زیر است:

x³+px+q=0

3

تا اینجا که همه چیز واضح است، ولی حل کلی این معادله تنزل یافته چیست؟ به شکل عمومی معادله درجه دوم توجه کنید:

x²+px+q=0

که جواب‌های آن بصورت زیر است:

بدلیل اینکه جذر یک عدد منفی، عددی حقیقی نیست، اگر p²-4q منفی باشد، جواب‌های این معادله اعداد مختلط خواهند بود. اگر p²-4q دقیقاً صفر باشد، هر دو جواب معادله یکسان خواهند بود؛ بنابراین از لحاظ عددی معادله تنها یک جواب دارد. و البته اگر p²-4q مثبت باشد، معادله دارای دو جواب خواهد بود که هر دو حقیقی هستند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 4

بازرگانی و رقابت

03/05/1401

4.1

یکی از آثار بدیع که در تاریخ ادبیات انگلیسی وجود دارد، کتاب ”قرن سیزدهم، بزرگترین قرن‌ها“ نوشته James J. Walsh است که در سال 1907 منتشر شد. بیشتر کتاب حاوی مدافعات استدلالی از مسیحیتِ کاتولیک است، ولی نویسنده کتاب تلاش کرده قرن سیزدهم را بعنوان دورانی ترسیم کند، که احیاء آموزش کلاسیک، و دست‌آورد‌های فرهنگی آن زیاد مورد توجه قرار نگرفته. قرن سیزدهم شروع ساخت کلیساهای جامع بزرگ، معماری گوتیک، و دانشگاه‌های اولیه بود. ظهور هنرمندانی همچون چیمابوئه (Cimabue) و جیاتو (Giotto)، دانشورانی همچون سنت‌فرانسیس و آکویناس (Aquinas)، دانته، پادشاهانی همچون لویی نهم، ادوارد اول، فردریک دوم، فرمان ماگنا کارتا (Magna Carta)، دوران جهانگردانی همچون مارکو پولو و اودوریکِ راهب (Friar Odoric)، که ظاهراً به لهاسا پایتخت تَبَت رسیده بود ... همه در قرن سیزدهم اتفاق افتاده بود. در دهه‌های اول همین قرن بود که لئوناردوی پیزایی، که بیشتر ما او را بعنوان لئوناردو فیبوناچی (Leonardo Fibonacci) می‌شناسیم شکوفا شد.

فیبوناچی یکی از چهره‌هایی است که نام او برای خیلی از افراد غیرریاضیدان نیز آشناست، و دلیلش هم دنباله‌ مشهوری است که به افتخار او نامگذاری شده:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, . . .

هر جمله از این دنباله مجموع دو جمله سمت چپ آن هستند: مثلاً 89 مجموع دو جمله قبلی خودش، یعنی 34 و 55 است. این دنباله، که در دائره‌المعارف اینترنتی اعداد صحیح، با عنوان A000045 شناخته می‌شود، آنقدر از لحاظ ریاضی و عِلمی اهمیت دارد، که یک نشریه فصلی بنام Fibonacci Quarterly به آن اختصاص یافته. عنوان یکی از شماره‌های این نشریه که در آگوست 2005 منتشر شد این بود: ”درون‌یابیِ پی-ییِ دنباله فیبوناچی توسط توابع ابر-هندسی“.

هرچند ممکن است از نظر کسانی که ریاضی نمی‌دانند چنین چیزی شگفت‌انگیز بنظر برسد، ولی در واقع به آسانی می‌توان nامین جمله این دنباله را با استفاده از فرمول زیر بدست آورد:

که مثلاً اگر n=4 باشد، فرمول فوق با استفاده از قضیه دوجمله‌ای به صورت زیر ساده خواهد شد:

که به آسانی می‌توان دید حاصل آن 3 است.

این دنباله ابتدا در کتابی بنام (Liber abbaci) که آن را لئوناردو نوشته بود پدیدار شد. این کتاب مربوط به مسئله تعداد خرگوش‌ها پس از زاد و ولد آنها است.

اگر یک جفت خرگوش داشته باشیم، و در هر ماه هر جفت از آنها تولید مثل کرده و یک جفت دیگر را تولید کنند، و جفت جدید پس از دو ماه قابلیت زایش داشته باشند، در پایان یک سال چند خرگوش خواهیم داشت؟

تنها راهی که من تاکنون توانسته‌ام این مسئله را تشریح کنم این بوده که ماه‌ها را بصورت A,B,C,D و غیره نامگذاری کنم. اولین جفتی که کار خودمان را با آن آغاز می‌کنیم، آن را به عنوان جفتِ A می‌نامیم. در ماه دوم ما هنوز جفت A را داریم، ولی همچنین جفت AB نیز، که حاصل تولید مثل جفت A هستند، به آنها اضافه شده، پس حالا دو جفت داریم. در ماه سوم جفت A دوباره جفت دیگری را تولید می‌کند، که ما آن را جفت AC می‌نامیم. جفت AB موجود است، ولی هنوز تولید مثل نکرده. حالا در ماه سوم کلاً سه جفت داریم. در ماه چهارم، یا ماه D، جفت A هنوز با ما است و جفت دیگری را تولید کرده، جفت AD. جفت AB نیز با ماست و حالا جفت خودش را تولید کرده، که ما آن را جفت ABD می‌نامیم. در این ماه جفت AC با ماست ولی به مرهله تولید مثل نرسیده. پس جفت‌هایی که ما داریم عبارتند از A, AD, AB, ABD, AC، که کلاً می‌شود پنج جفت ... و به همین ترتیب.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 5

تسلی خیال

10/05/1401

5.1

در طول دو قرن، یعنی از زمان سقوط قسطنطنیه در 1453 تا معاهده وستفالیا در 1648، دو پیشرفت مهم در جبر اتفاق افتاد. یکی از آنها حل معادلات درجه سوم و چهارم، و دیگری اختراع نمادنویسی امروزی است که ما برای نمایش اعداد و معادلات از آنها استفاده می کنیم.

همانطور که در فصل 4 گفته شد، اولین پیشرفت مابین سالهای1520 تا 1540 توسط ریاضیدانان شمال ایتالیا، با همکاری مشترک کاردانو و فِراری صورت گرفت.

دومین پیشرفت بزرگی که از آن یاد کردم، عمدتاً توسط دو ریاضیدان فرانسوی به نام‌های فرانسوا ویت (François Viete) (1540-1603) و رِنه دکارت (René Descartes) (1596-1650) صورت گرفت. این پیشرفت با پیشرفت دیگری نیز همزمان بود: کشف کُند اعداد مختلط، و قبول تدریجی آنها بعنوان یکی از ابزارهای استاندارد ریاضی. این پیشرفت آخر بیشتر جنبه حسابی داشت (یعنی با اعداد سر و کار داشت) تا جبری (یعنی با معادلات و چندجمله‌ای‌ها). ولی همانطور که دیدیم، اعداد مختلط از نیازهای جبری الهام گرفته شده بود. اگر شما یک چندجمله‌ای ساده نشدنی درجه سوم را رسم کنید (به شکل 6 در بخش ریاضی نگاه کنید)، به آسانی خواهید دید که سه جواب حقیقی دارد. بااینحال اگر شما برای معادله متناظر با آن از فرمول‌های جبری استفاده کنید و اعداد مختلط را نیز مجاز ندانید، این معادله هیچ جواب حقیقی نخواهد داشت!

دلایل دیگری برای وارد کردن اعداد مختلط به تاریخ جبر نیز وجود دارد. برای مثال، آنها اولین قدم برای یک مفهوم مهم جبری بنام استقلال خطی (linear independence) هستند، مفهومی که بعداً وقتی به نظریه بردارها و تانسورها رسیدم، آن را توضیح خواهم داد. اینها ابزارهایی هستند که فیزیک امروزی را ممکن کردند. اگر شما 3 را به 5 اضافه کنید، 8 را حاصل خواهید کرد: وقتی این دو عدد با هم جمع می‌شوند، سه‌گانگی 3 و پنج‌گانگی 5 مانند دو قطره آب در هشت‌گانگی 8 حل شده و دیگر اثری از 3 و 5 باقی نمی‌ماند. ولی اگر شما 3 را با 5i جمع کنید، حاصل آنها عددِ مختلطِ 3+5i خواهد بود، مانند مخلوط کردن یک قطر آب با یک قطره روغن. این همان استقلال خطی است.

بنابراین، من آنچه را که لازم است درباره کشف اعداد مختلط بدانید برای شما خواهم گفت. همانطور که در فصل 4 دیدید، اولین ریاضیدانی که این مخلوقات عجیب را با ترس و لرز بکار گرفت کاردانو بود. ولی اولین کسی که آنها را با اطمینان بکار گرفت رافائل بومبِلی (Rafael Bombelli) بود.

5.2

بومبِلی اهل بولونیا بود، یعنی همانجایی که دِل فرو در آنجا تدریس می‌کرد. او در همان سالی که دِل فرو فوت کرد (1526) بدنیا آمد. بنابراین او نسل بعدی کاردانو محسوب می‌شد. طبق معمول، چیزهایی که برای نسل‌های قبلی پذیرش آنها مشکل است، نسل‌های بعدی بهتر آنها را قبول می‌کنند. هنگامی که کتاب هنر والای کاردانو منتشر شد، بومبلی 19 ساله بود، یعنی همان سنی را داشت که بتواند تحت تاثیر این کتاب قرار گیرد.

بومبلی یک مهندس عمران بود. اولین کار مهمی که به او محول شده بود احیاء اراضی، که از 1449 تا 1560 طول کشید. این برای بومبلی موفقیت بزرگی به همراه آورد و نام او در این حرفه معروف گشت.

بومبلی عاشق کتاب هنر والا بود ولی احساس می‌کرد توضیحات کاردانو به اندازه کافی روشن نیستند. هنگامی که بومبلی در میانه دهه 20 زندگی خودش بود، تصمیم گرفت یک کتاب جبر بنویسد، کتابی که به مبتدیان کمک ‌کند در این موضوعات مهارت پیدا کنند. سرانجام او این کتاب را نوشت. عنوان کتاب ”جبر“ بود و چند ماه پیش از مرگش در 1572 منتشر شد، بنابراین می‌توان فرض کرد که او 25 سال مشغول کار روی این کتاب بوده.

در حدود سال 1560، بومبلی در رُم بود. در آنجا او با آنتونیو ماریا پازی (Antonio Maria Pazzi) ملاقات کرد، که در دانشگاه رُم ریاضی درس می‌داد. پازی در صحبت‌هایی که با بومبلی داشت به او گفته بود که در کتابخانه واتیکان کتابی را پیدا کرده که درباره حساب و جبر است و به یک نویسنده یونانِ باستان تعلق دارد که ”دیافانتوس“ نام دارد. این دو مرد کتاب را بررسی کردند و تصمیم گرفتند آن را ترجمه کنند. این ترجمه هرگز به پایان نرسید، ولی شکی نیست که بومبلی با مطالعه کتاب دیافانتوس از آن الهام فراوانی گرفته بود. او 143 مسئله‌ای را که در کتاب دیافانتوس بود در کتاب جبر خودش گنجانید، و از همین طریق بود که اولین بار آثار دیافانتوس به ریاضیدانان اروپا معرفی شد.

بخاطر دارید که گرچه دیافانتوس هیچ تصوری از اعداد منفی بعنوان اشیاء ریاضی نداشت و آنها را بعنوان جواب مسائل قبول نمی‌کرد، ولی اجازه می‌داد آنها حضورِ شَبَح‌واری در محاسبات میانی او داشته باشند، و به همین منظور قاعده علامت‌ها را فرمولبندی کرده بود. بنظر می‌رسد کاردانو نیز درباره اعداد مختلط نظر مشابه‌ای داشته، زیرا هیچ اشاره مستقیمی به آنها نمی‌کند، ولی برای گرفتن جواب‌های حقیقی از آنها استفاده می‌کند.

رویکرد بومبلی نسبت به اعداد منفی و مختلط جاافتاده‌تر بود. او نسبت به آنچه دیافانتوس گفته بود، قاعده علامت‌ها را روشن‌تر بیان می‌کند:

ضرب مثبت در مثبت می‌شود مثبت.

ضرب مثبت در منفی می‌شود منفی.

ضرب منفی در مثبت می‌شود منفی.

ضرب منفی در منفی می‌شود مثبت.

بومبلی در کتاب جبر خودش معادلات درجه سوم ساده نشدنی را گرفته، و جوابی را برای معادله x³=15x+4 پیدا می‌کند. او با استفاده از روش کاردانو، جواب زیر را حاصل می‌کند:

او با استفاده از برخی روش‌های مبتکرانه، ریشه‌های سوم عبارت بالا را، بترتیب بصورت و بدست می‌آورد. با جمع این دو، او جواب x=4 را حاصل می‌کند (دو جواب دیگر این معادله و هستند که او آنها را بدست نمی‌آورد).

اینجا اعداد مختلط شبیه اعداد منفی دیافانتوس هستند (یعنی تکنیکی برای بدست آوردن یک جواب حقیقی). آنها نوعی تسهیل کننده هستند. بومبلی آنها را بعنوان دستگاه‌هایی که جواب می‌دهند پذیرفته بود، و حتی برای آنها یک قاعده ضرب نیز ابداع کرد.

کتاب جبر بومبلی قدم بزرگی در فهم ریاضی بود، ولی او هنوز از فقدان یک نمادگذاری خوب رنج می‌برد. مثلاً او برای بیان فرمول زیر

همه آن را بصورت لفظی می‌نوشت. با اینکه فورمول نویسی بومبلی نسبت به نسل‌های پیشین خلاصه‌تر بود، ولی هنوز فاقد یک نمادنویسی مناسب بود.

5.3

قرن 16 برای فرانسویان قرن ناآرامی بود. بیشتر حکمرانی فرانسیس اول (1547-1515)، و بیشتر ثروت آن کشور صرف جنگ با کارل پنجم شده بود. بعد از آن هم فرانسویان کاتولیک و پروتستان دست به قتل عام یک دیگر زدند.

تا وقتی در سال 1598 پیمان نانت منعقد نشده بود، آنها به این کشت و کشتار ادامه دادند. در طول 36 سال، هشت جنگ داخلی میان فرانسویان اتفاق افتاد که با یک تغییر خاندان همراه بود (از خاندان والوا به بوربون در 1589). این جنگ‌ها صرفاً جنبه مذهبی نداشت، بلکه مخلوطی از عناصر مذهبی، طبقاتی، و سیاست‌های بین‌المللی در آن نقش داشتند. فیلیپ دوم پادشاه اسپانیا، که یکی از جنگ‌افروزان بزرگ بود، حداکثر تلاش خودش را کرد تا این منازعات ادامه یابند. تا جایی که به طبقه اجتماعی مربوط است، اوگنو‌ها (Huguenots)، یا همان پروتستان‌های فرانسه، در میان طبقه متوسط فرانسه طرفداران زیادی داشتند، ولی بیشتر طبقه نجبا نیز پروتستان بودند. ولی در مقابل، بیشتر روستاییان در اکثر نواحی کاتولیک باقی مانده بودند.

فرانسوا ویت (François Viète) در سال 1540 در یک خانواده پروتستان بدنیا آمد. او در سال 1560 مدرک حقوق خودش را از دانشگاه پواتیه گرفت. کمتر از دو سال بعد، جنگ‌های مذهبی فرانسه با قتل عام پروتستان‌ها در ناحیه واسی شروع شد.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 6

پنجه شیر

15/05/1401

6.1

هرچند جزیره بریتانیا در سال‌های (1651-1642) درگیر جنگ‌های داخلی، در طول سال‌های (1660-1651) درگیر دیکتاتوری نظامی، در 1668 درگیر یک انقلاب قانون اساسی، و دو تغییر خواندان (تئودور به استوارت‌ در 1603 و استوارت‌ به هانور در 1714) بود، ولی در طول قرون 16 تا 18 ریاضیدانان خوبی را پرورش داده بود.

من در فصل قبل به توماس هریوت اشاره کردم، که نمادگذاری پیچیده‌ای که او از آن استفاده می‌کرد تا مدتها نادیده گرفته شد (احتمالاً به غیر از دکارت). ریاضیدان اسکاتلندی جان نپر (John Napier) گرچه یک جبردان برجسته بحساب نمی‌آمد، ولی لگاریتم (logarithms) را اختراع کرد و در 1614 آن را به دنیا عرضه نمود. او همچنین استفاده از ممیز اعشاری را متداول کرد. ویلیام اوترد (William Oughtred) یک کتاب درباره جبر و مثلثات نوشت، و برای ضرب علامت را به ما معرفی کرد. جان والیس (John Wallis) اولین کسی بود که از تکنیک‌ها و نمادگذاری‌های دکارت برای هندسه تحلیلی استفاده کرد (ولی او طرفدار هریوت بود و عقیده داشت دکارت ایده‌های خودش را از هریوت گرفته).

ولی کلیه این اشخاص سرآغاز ورود آیزک نیوتون بودند. این مرد نابغه، که به گواه خیلی‌ها بزرگترین شخصیت در تاریخ علم است، در شب عید 1642 در لینکلن‌شایر انگلستان در یک خانواده ثروتمندِ کشاورز زاده شد. درباره مسیر زندگی، و همچنین شخصیت این مرد بسیار گفته و نوشته شده. در اینجا خلاصه‌ای از مقاله‌ای که خود من درباره او نوشتم را نقل می‌کنم:

داستان زندگی نیوتون خیلی جالب نیست. او هیچ وقت پایش را از شرق انگلستان بیرون نگذاشت. او در هیچ تجارت یا جنگی شرکت نکرد. برخلاف اینکه در دوره‌ای زندگی می‌کرد که بزرگترین حوادث تاریخی انگلستان در آن زمان اتفاق افتاده بود، به نظر می‌رسد او هیچ علاقه‌ای به مسائل سیاسی نداشته. حتی دوران کوتاه تصدی او بعنوان عضو پارلمان (که از طرف دانشگاه کمبریج صورت گرفت) نیز موجب نشد تا احساسات سیاسی در او برانگیخته شود. نیوتون هیچ ارتباط عاطفی با انسان‌های دیگر نداشت. بنابه ادعای خودش، که در آن خیلی تردید نیست، او در حالی مُرد که هنوز باکره بود. بطریق مشابه‌، او نسبت به رفاقت نیز بی‌تفاوت بود، و با می‌میلی با دیگران مکاتبه می‌کرد. بیشتر اوقات رابطه او و همتایانش با جر و بحث‌هایی همراه بود، ولی هیچ وقت به سطح دعوا نمی‌رسید.

ایزک نیوتون (1727-1642)

در اینجا نمی‌توانم از گفتن داستان مورد علاقه خودم درباره نیوتون خودداری کنم، هر چند فکر می‌کنم تکراری باشد. در سال 1696 ریاضیدان سوئیسی یوهان برنولی (Johann Bernoulli) دو مسئله دشوار را در برابر ریاضیدانان اروپا قرار داد. روزی که این مسائل به نیوتون نشان داده شدند، او آنها را حل کرد و جواب خودش را به انجمن سلطنتی لندن تسلیم کرد، و آنها نیز بدون اینکه بگویند چه کسی آنها را حل کرده، آن را برای برنولی فرستادند. به محض اینکه او جواب‌ها را دید متوجه شد که باید کار نیوتون باشد و گفت ”اینها جایِ پنجه شیری است که ما می‌شناسیم“.

این پنجه‌های قوی، خراش بزرگی در تاریخ جبر ایجاد کردند، خراشی که تا ابد جای آن باقی است.

6.2

نیوتون برای سهمی که در فیزیک دارد و همچنین اختراع حسابان معروف است، ولی بعنوان یک جبردان چندان شناخته شده نیست. در واقع او از سال 1673 تا 1683 در دانشگاه کمبریج جبر درس می‌داد و یادداشت‌های درسی خودش را به کتابخانه دانشگاه داده بود. سال‌ها بعد، هنگامی که او کار دانشگاهی را رها کرد و سرپرستی ضرابخانه سلطنتی را به عهده گرفت، جانشین او ویلیام وینستون این یادداشتها را بصورت کتابی به زبان لاتین، تحت عنوان حسابِ جامع (Universal Arithmetic) منتشر کرد. نیوتون با بی‌میلی اجازه انتشار این کتاب را داد. بنظر می‌رسید نیوتون هیچوقت از این کتاب خوشش نیامده بود. او اجازه نداد نامش بعنوان مؤلف در کتاب درج شود و حتی به فکرش افتاده بود تمامی نسخه‌های چاپ شده را بخرد تا آنها را بسوزاند. حتی در ترجمه انگلیسی این کتاب که در 1720 نیز منتشر شد، نام نیوتون بعنوان نویسنده نیامده است.

ولی چیزی که مورخین جبر را هیجان زده کرده بود، خود حسابِ جامع نبود، بلکه یادداشت‌های کوتاه نیوتون بود که در جوانی خودش مابین سال‌های 1665 تا 1666 نوشته بود و می‌شود آنها را در مجموعه آثار او پیدا کرد. آنها به زبان لاتین نیستند و به انگلیسی نوشته‌ شده‌اند، و با این کلمات آغاز می‌شوند:

هر معادله بصورت x⁸+px⁷+qx⁶+rx⁵+sx⁴+tx³+vxx+yx+z=0 دارای ریشه‌هایی بصورت ابعاد w^chy^e هستند، مجموع -p، مجموع مستطیل‌های هر یک +q، هر سه -r، هر چهارتا +s، ....

اینها بطور صریح حاوی هیچ قضیه‌ای نیست. ولی تلویحاً نشان دهنده یک قضیه است، و تئوری که بعدها بر اساس اینها بنا شد، چنان مهم بود که از آن بعنوان قضیه نیوتون یاد می‌کنند.

پیش از اینکه این قضیه را بیان کنم، باید مفهوم چندجمله‌ای‌ متقارن را توضیح دهم. برای بهتر فهمیده شدن موضوعات، من مثال خودم را به سه مجهول محدود می‌کنم، و آنها را α,β,γ می‌نامم. در زیر مثال‌هایی از چندجمله‌ای‌های متقارن با سه مجهول را می‌بینید:

...........................................

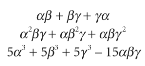
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

موضوعات ریاضی

ریشه‌های واحد

/21/05/1401

1

در بخش ریاضی مربوط به حل کلی معادلات درجه سوم، من به ریشه‌های سوم عدد 1 اشاره کردم. سه تا از این موجودات کوچک شیطانی وجود دارند. واضح است که خود 1 یکی از این ریشه‌ها است، زیرا 1×1×1=1. دو ریشه سومِ عدد 1، اعداد مختلط زیر هستند:

طبق عرف، بترتیب به آنها ω و ω² می‌گویند. با توجه به اینکه i²=-1، اگر شما هر کدام از این دو عدد را به توان 3 برسانید، حاصل آن 1 خواهد بود. بعلاوه، دومین عدد با مربع اولی مساوی است. معلوم است که ω² مربع ω می‌باشد. چیزی که کمتر واضح است این است که ω مربع ω² نیز هست (زیرا مربع ω² مساوی ω⁴ است، که برابر ω³ × ω، و طبق تعریف ω³=1 است.)

2

مطالعه ریشه‌های nام عددِ 1 (که اغلب به آن ریشه‌های واحد گفته می‌شود)، بسیار جذاب است و در بسیاری از حوزه‌های مختلف ریاضی، از جمله هندسه کلاسیک و نظریه اعداد، رسوخ کرده است. چنین چیزی فقط وقتی امکانپذیر شد که اعداد مختلط مورد قبول اکثر ریاضیدانان قرار گرفتند، یعنی تقریباً از اواسط قرن 18. ریاضیدان بزرگ سوئیسی لئونارد اویلر (Leonhard Euler) در کتابی بنام ”استخراج ریشه‌ها و کمیت‌های غیرگویا“ که در 1751 منتشر کرد، این موضوع را بخوبی گسترش داد.

ریشه‌های دوم عدد 1 اعداد 1 و -1 هستند. ریشه‌های سوم 1 عبارتند از 1 و دو عدد ω و ω² که دربالا به آنها اشاره کردم. ریشه‌های چهارم 1 عبارتند از 1، -1، i، و -i. اگر شما هر کدام از این چهار عدد را به توان 4 برسانید، حاصل آن برابر 1 خواهد بود. اویلر ریشه‌های پنجم واحد را بصورت زیر نشان داد:

اگر بخواهیم این اعداد را بصورت اعشاری تخمین بزنیم، عبارت خواهند بود از

1, 0.309017 + 0.951057i, -0.809017 + 0.587785i,

-0.809017 - 0.587785i, 0.309017 - 0.951057i

اگر آنها روی یک صفحه مختلط معمولی رسم کنید، قسمت حقیقی آنها از چپ به راست و قسمت موهومی آنها از بالا به پایین قرار خواهند گرفت (شکل 1).

شکل 1. ریشه‌های پنجم واحد.

در واقع آنها رئوس یک پنج‌ضلعی منظم هستند که مرکز آن در مبداء قرار دارد. به عبارت دیگر، آنها روی محیط دایره‌ای با شعاع واحد قرار دارند (دایره‌ای با شعاع 1) و محیط دایره را به پنج کمان مساوی تقسیم. اصطلاحی که برای اینکار وجود دارد سایکلوتومیک (cyclotomic)، یا دایره‌بُری، است. این اعداد مختلط (نقاطی که روی صحفه مختلط رسم شده‌اند)، نقاط دایره‌بُر (cyclotomic points) نامیده می‌شوند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 7

یورش به معادلات درجه پنجم

/22/05/1401

7.1

در فصل 4 توضیح دادم که چگونه در نیمه اول قرن شانزدهم ریاضیدانان ایتالیایی توانستند راهی برای حل کلی معادلات درجه سوم و چهارم پیدا کنند. روشن بود که چالش بعدی حل کلی معادلات درجه پنجمی بود که بصورت زیر هستند:

x⁵+px⁴+qx³+rx²+sx+t=0

اجازه دهید به خواننده یادآوری کنم که در اینجا ما به دنبال چه هستیم. برای هر معادله درجه پنجمِ خاص، ما می‌توانیم با استفاده از تکنیک‌هایی مشابه آنچه ریاضیدانان مسلمان در قرون 10 و 11 از آن استفاده می‌کردند، برای معادلات درجه پنجم (یا هر درجه‌ای) یک جواب عددی را بدست آوریم که با هر درجه‌ای از تقریب که بخواهیم دقیق باشد. چیزی که نامعلوم بود پیدا کردن یک روش جبری بود، جوابی بصورت

x=[p,q,r,s,tیک عبارت جبری بر حسب ضرائب معادله، یعنی ]

در اینجا لغت ”جبری“ به معنای ”فرمولی است که فقط شامل جمع، تفریق، ضرب، تقسیم، توان، و ریشه‌گیری باشد (ریشه دوم، سوم، چهارم، پنجم، ...)“. برای تکمیل مطلب، باید بگویم آنچه در بالا ذکر شد، فقط باید حاوی تعداد متناهی از این عملیات باشد. آنچه در اینجا به دنبال آن هستیم، شبیه فرمولی است که در بخش مربوط به حل کلی معادلات درجه چهارم آمده بود، ولی ممکن است نسبت به آن پیچیده‌تر باشد.

حالا ما می‌دانیم که چنین راه‌حلی وجود ندارد. تا آنجا که من بررسی کردم، اولین کسی که اعتقاد داشت چنین است (یعنی معادله درجه پنجم هیچ راه حل جبری ندارد)، یک ریاضیدان ایتالیایی دیگر بنام پائولو روفینی (Paolo Ruffini) بود، که در اواخر قرن 18 به این نتیجه رسید، و اثباتی را نیز برای آن ارائه کرد (گاوس هم در رساله دکترای خودش چنین چیزی را مطرح کرد ولی اثباتی را برای آن ارائه نداد). روفینی در سالهای 1803، 1808، و 1813 برای این مسئله سه اثبات دیگر را نیز ارائه داد، ولی هیچکدام از آنها نتوانست ریاضیدانان دیگر را قانع کند، و تا آنجایی که معلوم است آنها حتی اعتنایی هم به آن نکردند. کسی که برای حل‌ناپذیریِ جبریِ معادلاتِ درجه پنجم اثباتی را ارائه داد، و اعتبار قطعی آن را گرفت، ریاضیدان نروژی نیلز هنریک آبل (Niels Henrik Abel) بود که اثبات خودش را در 1824 منتشر کرد.

پائولو روفینی (1822-1765)

در تمامی قرن 18 عملاً این عقیده وجود داشت که حل عمومی معادلات درجه پنجم از طریق جبری امکان‌پذیر است. ولی یافتن این راه‌حل، باید بسیار پیچیده باشد. هرچه باشد، در سال 1700 حدود 160 سال از حل معادلات درجه چهارم توسط فِراری می‌گذشت، و درمورد معادلات درجه پنجم هیچ پیشرفتی حاصل نشده بود. تکنیک‌هایی که برای حل معادلات درجه سوم و چهارم مورد استفاده قرار گرفته بود، هیچ تاثیری روی معادلات درجه پنجم نداشتند. روشن بود که برای حل این معادلات به ایده‌های جدیدی نیاز بود.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

موضوعات ریاضی

فضاهای برداری و جبرها

/11/06/1401

1

تاریخچه مفهوم بردار (vector) در ریاضیات تا حدودی درهم برهم است. من سعی می‌کنم تا آنجا که بتوانم آن را باز کنم. تمامی آنچه که در این بخش خواهد آمد، برداشت نوینِ از بردار است که بر اساس ایده‌ها و اصطلاحاتی هستند که از حوالی سالهای 1920 در جریان بوده.

2

فضای برداری (Vector space) یا فضای خطی، یک شیء ریاضی است. این شیء در خودش دو نوع عضو دارد: بردار و اسکالر. اسکالرها (scalars) می‌توانند برخی از دستگاه‌های آشنای عددی باشند، همراه با عملیات کامل جمع، تفریق، ضرب، و تقسیم، که مثلاً ℝ (دستگاه اعداد حقیقی) یک نمونه خوب از آن است. بردارها کمی پیچیده‌ترند.

اجازه دهید یک مثال خیلی ساده از یک فضای برداری را به شما ارائه دهم. یک صفحه تختِ بی‌نهایت را درنظر بگیرید. من نقطه خاصی را در این صفحه انتخاب می‌کنم و آن را مبداء (origin) می‌نامم. یک بردار خطی است که از نقطه مبداء به نقطه دیگری می‌رود. شکل 1 چند بردار را نشان می‌دهد. شما می‌توانید ببینید که یک بردار دو مشخصه دارد، که یکی طول آن و دیگری جهت آن است.

در این فضای برداری، هر بردار دارای یک معکوس است. عکس یک بردار، برداری است که طول آن یکی ولی به جهت مخالف اشاره کند (به شکل 2 نگاه کنید). خود مبداء بعنوان یک بردار محسوب می‌شود که بردار صفر نام دارد.

شکل 1: چند بردار.

شکل 2: دو بردار معکوس هم.

شکل 3: جمع دو بردار

دو بردار را می‌توان با هم جمع کرد. برای جمع دو بردار، باید آنها را بعنوان اضلاع مجاور یک متوازی‌الاضلاع در نظر بگیرید. در اینصورت جمع آنها، قطر متوازی‌الاضلاع است که از مبداء به سوی گوشه دیگر رسم می‌شود (به شکل 3 نگاه کنید).

اگر شما برداری را با بردار صفر جمع کنید، حاصل آن همان بردار اولیه است. اگر شما برداری را با معکوس آن جمع کنید، حاصل آن بردار صفر است.

هر بردار را می‌توان در یک اسکالر ضرب کرد. با اینکار طول بردار به میزانی متناسب با مقدار اسکالر تغییر خواهد کرد (برای مثال اگر اسکالر 2 باشد، طول بردار دو برابر خواهد شد)، ولی جهت آن تغییر نخواهد کرد (مگر اینکه مقدار اسکالر منفی باشد، که در اینصورت جهت بردار عکس می‌شود).

3

این خلاصه‌ای بود از مفهوم فضای برداری. البته فضای برداریِ صفحه-تختی که در اینجا ارائه کردم فقط نمونه‌ای از آن بود. مطالب بیشتری درمورد فضاهای برداری وجود دارد که بعداً سعی خواهم کرد آنها را بیان کنم. ولی فعلاً آنچه گفتم برای ما کافی است.

یک ایده مهم در فضای برداری مفهوم وابستگی خطی (linear dependence) است. در فضای برداری خودتان، هر مجموعه‌ از بردارها را که می‌خواهید انتخاب کنید، و فرض کنید نام آنها u,v,w,… و غیره باشد. اگر بتوان اسکالرهایی مثل p,q,r,… را چنان پیدا کرد که همه آنها صفر نباشند و رابطه زیر برقرار باشد:

pu+qv+rw+. . .=0 (یعنی همان بردار صفر)

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 8

جهش به بُعد چهارم

/12/06/1401

8.1

حقیقتاً ادبیات ریاضی-تخیلی بخش مهمی از ادبیات را تشکیل نمی‌دهد. یکی از معدود آثاری که توجه دیرپایی را به خودش جلب کرده، کتاب تختستان[3] (Flatland) نوشته ادوین اَبوت است که در 1884 منتشر شد و بعد از گذشت 140 سال، هنوز هم تجدید چاپ می‌شود.

تختستان توسط موجودی روایت می‌شود که خودش را ”یک مربع“ می‌نامد. او درواقع مربعی است که در درون یک جهان دو-بُعدی زندگی می‌کند، و عنوان کتاب هم حاکی از چنین دنیایی است. در تختستان موجوداتِ زنده دیگری نیز زندگی می‌کنند که همه آنها شکلی دو-بُعدی دارند که از لحاظ نظم، زوايا و اضلاع مختلفی دارند: مثلث‌هایی از گونه متساوی‌الساقین (که فقط دو ضلع با هم مساویند) و متساوی‌الاضلاع (که هر سه ضلع با هم مساویند)، مربع‌ها، پنج‌ضلعی‌ها، شش‌ضلعی‌ها، و غیره. در آنجا یک نظامِ مراتبِ اجتماعی برقرار است که موجودی که تعداد اضلاع آن بیشتر باشد، مرتبه او نیز بالاتر است، و دایره در بالاترین مرتبه قرار دارد (چون درواقع دایره یک بی‌نهایت ضلعی است). زنان فقط پاره‌خط‌هایی هستند که مشمول عدم‌کارایی و تبعیض‌های مختلف‌اند!

اولین بخش کتابِ تختستان به شرح این سرزمین و مراتب اجتماعی آن می‌پردازد. قسمت عمده‌ای از آن به موضوع پیچیده تشخیص مرتبه اجتماعی یک غریبه اختصاص دارد. بدلیل اینکه شبکیه چشمِ ساکنان تختستان یک-بعدی است (درست مانند اینکه از انسانها دو-بعدی است)، اشیائی که در میدان دید او قرار دارند فقط پاره‌خط‌ها هستند، و شکل واقعی یک غریبه (و بنابراین مرتبه اجتماعی او) بیشتر توسط لمس کردن حاصل می‌شود. بنابراین شکل معمول معارفه این است که بگوییم ”اجازه دهید آقای فلان را به شما حس کنم!“

در نیمه دوم کتاب، مربع ما جهان‌های دیگری را کشف می‌کند. او در یکی از خواب‌های خودش، از خطستان دیدار می‌کند، مکانی تک-بعدی، که نویسنده کتاب 11 صفحه را برای توصیف آن اختصاص داده. بدلیل اینکه یک خطستانی هیچ وقت نمی‌تواند از هیچ طرفی از همسایه خودش گذر کند، گسترش گونه‌ها مشکلات مختلفی را بروز می‌دهد که ابوت با ظرافت و نبوغ بسیاری آنها را حل می‌کند.

سپس مربع در سرزمین خودش، یعنی تختستان، از خواب بیدار می‌شود و در آنجا با موجودی از بُعد سوم دیدار می‌کند: این موجود یک کُره است که با فرو کردن کم و بیش خودش در تختستان، موجب آزار ساکنان می‌شود. هر زمان که او خودش را در تختستان فرو می‌کند، از دید مربع مثل دایره اسرارآمیزی بنظر می‌رسد که هر بار بزرگتر و کوچکتر می‌شود. این کره، مربع ما را درگیر یک گفتگوی فلسفی می‌کند، و در مقطعی از این گفتگو، او را با نقطه‌ستان آشنا می‌کند، فضایی که بُعد آن صفر است، و ساکن این سرزمین را اینطور توصیف می‌کند ” درحالی که هیچ نیست، خودش یگانه و کُل خودش است. با اینحال بطور کامل از خود راضی است، پس این درس را بیاموز که از خود راضی بودن همان پست و نادان بودن است، و آرزو داشتن، بهتر از کور و جاهلانه خوش بودن است.“ فکر می‌کنم که همه با ما چنین موجوداتی برخورد داشته‌ایم.

هنگامی که تختستان منتشر شد، ابوت هنوز 46 سال بیشتر نداشت. در مدخلی که در دائره‌المعارف بریتانیا چاپ 1911 تحت نام او آمده، او را اینطور توصیف می‌کند: ” معلم و خداشناس انگلیسی.“ در اینجا هیچ اشاره‌ای به تختستان نمی‌شود. درواقع ابوت مدیر یک مدرسه پسرانه بود که اندیشه‌هایی مترقی و اصلاح‌طلبانه داشت. تفکرات او براساس دیدگاه‌های شخصی او نسبت به مسیحیت، و تردید نسبت به بسیاری از رسوم جامعه عصر ویکتوریا شکل گرفته بودند. از یک لحاظ، تختستان نوعی هجونامه اجتماعی بود.

از حدود 140 سالی که از انتشار تختستان می‌گذرد، این کتاب توجه تعداد بیشماری از خوانندگان را به خودش جلب کرده و قوه تخیل آنها را به حرکت درآورده. کتاب‌های مثل کره‌ستان (Sphereland) نوشته Dionys Burger یا تخت‌ترستان (Flatterland) نوشته یان استوارت از کتابهایی هستند که بر اساس ایده اصلی ابوت نوشته شده‌اند. فیزیک، شیمی، و فیزیولوژی موجودات دو بعدی - موضوعاتی که ابوت به آنها کمتر پرداخته، یا اگر هم پرداخته زیاد قانع کننده نیستند -توسط ریاضیدان کانادایی ا.ک دودنی (Dewdney) در کتابی بنام جهان‌سطح (Planiverse) که در سال 1984 منتشر شد بخوبی مورد بررسی قرار گرفته‌اند. ولی کتابی که ارزش ادبی کمتری دارد، ولی از جهاتی بیشتر در خاطر می‌ماند، داستان کوتاه ”پیام یافت شده در نسخه‌ای از تختستان“، نوشته ریاضیدان آمریکایی رودی راکر (Rudy Rucker) است، که در واقع قهرمان داستان در زیر زمین یک رستوران پاکستانی در لندن با اهالی تختستان روبرو می‌شود. نهایتاً داستان به این می‌انجامد که او تختستانی‌ها را می‌خورد و می‌گوید آنها ”طعم ماهی دودی مرطوب می‌دهند!“

در اینجا ما با فضاهایی روبرو می‌شویم که صفر، یک، دو، و سه بُعد دارند، ولی چرا باید به اینها بسنده کرد؟ احتمالاً بیشتر کسانی که اهل ریاضیات نیستند از طریق داستان اچ. جی. ولز، بنام ماشین زمان درباره بعد چهارم می‌شنوند، که در آن قهرمان داستان می‌گوید:

فضا، آنطور که ریاضیدانانِ ما از آن صحبت می‌کنند، دارای سه بُعد است، که می‌توانیم آنها را طول، عرض، و ضخامت بنامیم، و همیشه با ارجاع به سه صفحه عمود بر هم قابل تعریف است. ولی برخی از مردم که گرایش‌های فلسفی دارند این سئوال را مطرح می‌کنند که چرا ما بطور خاص سه بُعد داریم؟ چرا بُعد دیگری نداشته باشیم که عمود بر این سه بُعد فعلی باشد؟ و حتی تلاش‌ نکنیم یک هندسه چهار-بُعدی بسازیم؟

حتی امروز هم مدتی طول می‌کشد تا نظریات پیچیده جای خودشان را در ادبیات عامه باز کنند. اگر ادبای دهه 1880 و 1890 آثار عامه پسندی درباره تعداد ابعاد فضا می‌نوشتند ، ما می‌توانیم مطمئن باشیم که ریاضیدانان حرفه‌ای خیلی پیش از اینها در میان خودشان چنین سئوالاتی را مطرح کرده بودند.

از اواخر نیمه اول قرن نوزدهم، کم و بیش ایده‌هایی درباره تعداد ابعاد فضا برای ریاضیدانان مطرح بود. در اوایل نیمه دوم قرن نوزدهم، این باران‌های کوتاه و گاه‌ به ‌گاه، ناگهان به یک رگبار تبدیل شدند، و به ریاضیدانان بزرگی همچون فلیکس کلاین (Felix Klein) اجازه دادند تا چنین واپس‌نگری را داشته باشد و بگوید: ”در حوالی سال 1870، مفهوم فضای n-بعدی به دارایی‌های عام ریاضیدانان نسل جدید تبدیل شد.“

این ایده‌ها از کجا آمدند؟ در ابتدای قرن نوزدهم هیچ اثری از آنها نیست. ولی در انتهای آن قرن، چنان گسترده شدند که حتی راه خودشان را به ادبیات تخیلی عامه‌پسند باز کردند.

8.2

در دهه‌های آغازین قرن نوزدهم، ایده‌های کاملاً بالغی درمورد اعداد مختلط مطرح شده بود که بطور طبیعی در دورنمای ذهنی ریاضیدانان قرار گرفته بود. همانطور که در ابتدای این کتاب شرح دادم، در آن زمان مفهومِ امروزی عدد کم‌ و بیش در ذهن ریاضیدانان جا افتاده بود (هر چند استفاده از ”حروف توخالی“ برای آنها به اواخر قرن باز می‌گردد).

به ویژه، استفاده از نمودارهای تصویری برای نشان دادن اعداد حقیقی و مختلط بعنوان نقاط روی یک خط، و نقاط پراکنده روی یک صفحه تخت، بخوبی متداول بودند. قدرت شگرف اعداد مختلط و فواید آنها در حل طیف وسیعی از مسائل ریاضی، بطور گسترده‌ای مورد تقدیر بود. هنگامی که همه اینها نهادینه شدند، سئوالات زیر پیش آمد.

اگر گذر از اعداد حقیقی که صرفاً تک-بُعدی هستند، به اعداد مختلط، که دو بُعدی هستند، چنان بر قدرت و درک ما می‌افزاید، چرا اینجا متوقف شویم؟ آیا ممکن نیست اعداد دیگری باشند که در انتظار بکارگیری باشند؟ ( مثلاً اعداد ابر-مختلط) که طریقه نمایشِ طبیعی آنها سه-بُعدی باشد؟ و این امکان وجود داشته باشد که آنها با خودشان درک گسترده‌تری از ریاضیات را به همراه داشته باشند؟

از اواخر قرن هجدهم، این سئوال ذهن بسیاری از ریاضیدانان را به خودش مشغول کرده بود (از جمله گاوس) ولی پی‌آمدهای قابل ملاحظه‌ای نداشت. در حوالی سال 1830، همین سئوال برای ویلیام روان همیلتون پیش آمد.

8.3

داستان زندگی همیلتون غم‌انگیز است. اما اینطور نیست که زندگی او به طریقی فلاکت‌بار بوده باشد - مثلاً تحت تاثیر جنگ، فقر، یا بیماری قرار گرفته باشد. همچنین هیچ نشانی از بیماری‌های ذهنی - مثل افسردگی مزمن، نیز در او مشاهده نشده بود. حتی دچار مشکلات مالی و شغلی هم نشده بود. چیزی که در مورد او بیشتر صدق می‌کند این است که زندگی همیتون در یک مسیر رو به زوال قرار گرفت. او در کودکی یک اعجوبه شگفت‌انگیز بود؛ در جوانی تنها یک نابغه بود؛ در میان سالی، تنها درخشان بود؛ و در سالهای آخر عمرش، یک آدم مست و ملال‌آور.

درباره استعداد ریاضی همیلتون جای هیچ شکی نیست. او بینش ریاضی فراوانی داشت و تلاش می‌کرد تا آن بینش را بر روی مشکل‌ترین مسائل زمان خودش متمرکز کند. امروزه ریاضیدانان برای او احترام زیادی قایل هستند و یاد او را گرامی می‌دارند.

هم ایرلندی‌ها و هم اسکاتلندی‌ها، همیلتون را به خودشان متعلق می‌دانند زیرا او در شهر دابلین از یک والدین اسکاتلندی بدنیا آمد، ولی او خودش را یک ایرلندی می‌دانست. در کودکی او یک اعجوبه بود، و تا 13 سالگی تعداد زیادی از زبان‌های دنیا را می‌دانست، و ادعا می‌کرد هر سال می‌تواند به یک زبان تسلط پیدا کند.

ویلیام روان همیلتون (1865- 1805)

او در پاییز 1823 به ترینیتی کالج دابلین رفت، جایی که خودش را بعنوان استاد ادبیات کلاسیک به بقیه شناساند. ولی در پایان همان سال با کاترین دیسنی آشنا و عاشق او شد. خانواده کاترین فوراً او را به مرد دیگری که بیشتر واجد شرایط بود شوهر دادند، و این عشق از دست رفته باعث تباهی زندگی او، و شاید هم کاترین شد. همیلتون بعداً در 1833 با یک زن رنجور و نامرتب ازدواج کرد، ازدواجی که تا آخر عمرش از آن در عذاب بود.

همیلتون از همان سالهای نوجوانی ریاضیات را انتخاب کرده بود، طوری که سریعاً در آن استاد شده بود، و با بالاترین نمره در علوم، و همچنن ادبیات کلاسیک، از کالج ترینیتی فارغ‌التحصیل شد، موفقیتی که قبلاً کسی به آن دست نیافته بود. در سال‌های آخر عمرش، او ”تابع مشخصه“ (characteristic function) را معرفی کرد که منبع نهایی عملگر همیلتونی است و برای نظریه کوانتومِ نوین بسیار اساسی است.

همیلتون در 1827 بعنوان استاد ستاره‌شناسی در کالج ترینیتی برگزیده شد. مانند همه ریاضیدانان آن دوره، همیلتون نیز به قدرت شگرف اعداد مختلط پی برده بود. در 1833 او مقاله‌ای را منتشر کرد که در آن به طریقی کاملاً جبری با دستگاه اعداد مختلط برخورد شده بود، چیزی که درواقع امروز ما آن را ”یک جبر“ (an algebra) می‌نامیم. همیلتون عدد مختلط a+bi را فقط بصورت (a,b) می‌نوشت. دراینصورت قاعده ضرب اعداد مختلط بصورت زیر بود:

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 9

دترمینان‌ها و ماتریس‌ها

/16/06/1401

9.1

اینجا یک مسئله لفظی را بیان می‌کنم. در این مسئله از سه نوع دانه نام برده می‌شود، و فکر می‌کنم اگر سه نوع دانه را بعنوان سه رنگ قرمز، آبی، و زرد در نظر بگیریم، تجسم آنها آسانتر می‌شود.

مسئله: سه نوع دانه وجود دارند. از دانه اول سه سبد، از دانه دوم دو سبد، و از دانه سوم یک سبد داریم، که روی هم 39 واحد وزن دارند. دو سبد از دانه اول، سه سبد از دانه دوم، و یک سبد از دانه سوم روی هم 34 واحد وزن دارند. و یک سبد از دانه اول، دو سبد از دانه دوم، و سه سبد از دانه سوم روی هم 26 واحد وزن دارند. وزن هر یک از سبدهای دانه چقدر است؟

بیایید فرض کنیم که وزن یک سبد از دانه‌های قرمز x، وزن یک سبد از دانه‌های آبی y، و وزن یک سبد از دانه‌های سبز z است. بنابراین من برای تعیین وزن این سه سبد باید دستگاه معادلات خطی همزمانِ زیر را را برای x، y، و z حل کنم:

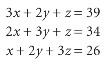
به سادگی می‌توان بررسی کرد که جواب‌ها آن عبارتند از x=³⁷/₄، y=¹⁷/₄، و z=¹¹/₄.

نه دیافانتوس و نه ریاضیدانان بابِلِ باستان هیچ مشکلی در حل این مسئله نداشتند. دلیلی که این مسئله جایگاه برجسته‌ای در تاریخ ریاضیات دارد این است که طرح کننده آن یک روش باقاعده برای حل این مسئله، و مسائل مشابه با هر تعداد از مجهول، توسعه داده، روشی که هنوز هم به مبتدیانِ جبرِ ماتریسی آموخته می‌شود. و همه اینها به 2000 سال قبل باز می‌گردد.

ما نام ریاضیدانی که این روش را ابداع کرده نمی‌دانیم. او مؤلف کتابی بنام ”نُه فصل درباب هنر محاسبه“ بود. این کتاب حاوی 246 مسئله درباره اندازه‌گیری و محاسبه بود. این کتاب تاثیر گذارترین اثر در ریاضیاتِ چینِ باستان بود. تاثیر دقیق این کتاب بر روی توسعه ریاضیات هندی، ایرانی، اسلامی، و اروپایی خیلی مورد بحث است، ولی از قرونِ اولیه میلادی، نسخه‌هایی از این کتاب در سراسر شرق آسیا در گردش بود، و با توجه به داد و ستدها و تماس‌هایی که در قرون وسطی در سراسر اُروسیا انجام می‌گرفت، تعجب آور نیست که برخی از ریاضیدانان غرب-آسیا از آن الهام گرفته باشند.

با توجه به شواهد درونی و توضیحاتی که در نسخه‌های آخری این کتاب توسط ویرایستاران نوشته شده، ما می‌توانیم تاریخ انتشار نسخه اولیه کتاب نُه فصل را در زمان سلسلهِ هان (Han) بدانیم، که از 202 پ.م تا 220 ب.م بود. این زمان یکی از پرشکوه‌ترین دوران‌ها در تاریخ چین است، که در آن امپراطوری چین برای اولین بار بر بیشتر چین امروزی تسلط داشت، و این سرزمین قطعاً توسط حکمرانان بی‌باک بومی متحد شده بود.

درواقع چین قبلاً توسط امپراطور مخوف اول، در سال 221 پ.م در زمان سلسله چین[4] (Qin) متحد شده بود. ولی 11 سال پس از مرگ این حکمران ظالم، وضعیت سیاسی سلسلهِ چین سریعاً از هم پاشید. پس از آن سال‌ها جنگ داخلی درگرفت تا اینکه یکی از جنگ‌سالاران بنام لیو بنگ از بقیه حریفانش پیشی گرفت و در 202 پ.م سلسله هان را تاسیس کرد.

یکی از کارهای معروف حکمرانان سلسله چین، سوزاندن کتابها بود. طبق تعالیم صریح فیلسوفِ تمامیت‌خواهی بنام شانگ یانگ، امپراطور چین فرمان داده بود تا کلیه کُتبِ فلسفهِ نظری باید برای سوزاندن به ماموران دولت تحویل داده شوند. خوشبختانه در آن دوره آموزش بصورت طوطی‌وار و حفظ‌ کردنی انجام می‌گرفت، بنابراین پس از انحلال سلسله چین، ادیبان توانستند متون از دست رفته را از حافظه خودشان بیرون کشیده و دوباره آنها روی کاغذ بی‌آورند. احتمالاً کتاب نُه فصل نیز به همین شکل تولید شده بود. شاید هم حکمرانِ ظالم این کتاب را که به کشاورزی و موضوعات عملی دیگر مربوط بود، از سوزاندن معاف کرده بود، بنابراین اگر هم کتاب نه فصل پیش از سلسله هان وجود داشته، احتمالاً جزء کتابهایی بوده که سوزانده نشده بودند.

به هر حال شروع دودمان هان در چین، زمانِ خلاقیتِ ریاضی بود. صلح با خودش تجارت به همراه آورده بود، که به مهارت‌های محاسبه‌ نیاز داشت. استاندارد کردن اوزان و اندازه‌ها در سلسله چین شروع شد، و به علاقه به محاسبه مساحت‌ها و حجم‌ها منجر شد. استقرار آئين كنفوسيوس بعنوان پایه عقیدتی حکومت، به یک تقویم قابل اتکا نیاز داشت تا توسط آن رسوم مذهبی بتوانند در موعد مقرر انجام شوند. به همین جهت تقویمی بر اساس دوره‌های 19-سالهِ معمول ساخته شد.

احتمالاً کتاب نُه فصل یکی از ثمرات این خلاقیت بود. قطعاً این کتاب در قرن اول میلادی وجود داشت و نقش مهمی در آیندهِ فرهنگِ ریاضی چین بازی کرد، نقشی که می‌توان آن را با تاثیر کتاب اصولِ اقلیدس در اروپا مقایسه کرد. و مسئله اندازه‌گیری وزن دانه‌ها که قبلً آن را توضیح دادم، در فصل هشتم این کتاب آمده است.

نویسنده کتاب نُه فصل چگونه این مسئله را حل کرده بود؟ در مرحله اول، معادله دوم را در 3 ضرب کرده بود (که آن را به 6x+9y+3z=102 تبدیل می‌کند)؛ سپس معادله اول را 2 بار از این کم کرد. بطور مشابه، معادله سوم را در 3 ضرب کرد (که معادله 3x+6y+9z=78 را می‌دهد) و یک بار معادله اول آن را از کم کرد. حالا مجموعه این سه معادله به صورت زیر در خواهد آمد:

حالا معادله سوم را در 5 ضرب کنید (که آن را بصورت 20y+40z=195 در می‌آورد) و معادله دوم را چهاربار از آن کم کنید. با اینکار معادله سوم بصورت زیر ساده می‌شود:

36z=99

که اگر آن را حل کنیم، z=¹¹/₄ خواهد بود. اگر این مقدار را در معادله دوم بگذاریم، مقدار y بدست خواهد آمد، و اگر این دو مقدار را در معادله اول بگذاریم، مقدار x بدست خواهد آمد.

همانطور که گفتم این روش بسیار کلی است و می‌تواند نه فقط برای دستگاه‌هایی شامل سه معادله و سه مجهول، بلکه برای دستگاه‌هایی با چهار معادله‌ و چهار مجهول، پنج معادله و پنج مجهول، و غیره بکار گرفته شود.

حالا این روش به روش حذف گاوسی (Gaussian elimination) معروف است. میان سال‌های 1803 و 1809، گاوس سیارک پالاس را چند بار رسد کرده بود، و می‌خواست مدار آن را محاسبه کند. برای انجام اینکار باید دستگاهی از معادلات حل می‌شد که شامل شش معادله خطی و شش مجهول بودند. گاوس نیز با این مسئله به همان روشی برخورد کرد که من در بالا انجام دادم، و این دقیقاً همان روشی که 2000 سال قبل نویسنده گمنام کتابِ نُه فصل درباب هنر محاسبه بکار گرفته بود.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 10

سرزمین مه‌‌گرفته بریتانیا

/22/06/1401

10.1

در زیر تکه‌ای از مقدمه کتاب رساله‌ای بر جبر نوشته ریاضیدان انگلیسی جورج پیکاک را می‌بینید، که در 1830 چاپ شده:

حساب را تنها می‌توان بعنوان علمی در نظر گرفت که اصول و عملیات آن با جبر موافق باشد، ولی اینکه با کدام یک از آنها، این نه محدود است و نه معین.

ده سال بعد ریاضیدان جوان اسکاتلندی دانکن گرگوری، که زیر نظر پیکاک تحصیل کرده بود چنین می‌نویسد:

جبر معمولی شامل تعدادی از قضایا است که ظاهراً صحت آنها تنها برای علائمی که نشان دهنده اعداد هستند اثبات شده، ولی می‌توان آنها را برای طیف گسترده‌تری نیز بکار گرفت. چنین قضایایی تنها به قوانین ترکیب بستگی دارند که موضوع آنها علائم هستند، و بنابراین ماهیت این علائم هرچه باشد، این قوانین برای همه آنها درست هستند.

و در زیر نیز تکه‌ای از کتاب ”مثلثات و جبر مضاعف“ نوشته آگوستوس دِمورگان را می‌بینید که در 1849 منتشر شد:

فرض کنید علائم M، N، +، و همچنین یک قانون برای ترکیب این علائم داده شده باشد، که مثلاً M+N با N+M برابر است. این محاسبه‌ای با علائم است. چگونه می‌توان آن را به یک چیز مهم بدل کرد؟ به طرق مختلف، که یکی از آنها چنین است: 1- ممکن است M و N اندازه چیزی باشند و + نیز علامتِ اضافه‌ کردن دومی به اولی باشد. 2- ممکن است M و N عدد باشند و + نیز علامتِ ضربِ اولی در دومی باشد. 3- ممکن است M و N خط باشند، و + نیز علامتی برای ساختن یک مستطیل از این دو خط باشد که اولی طول و دومی عرض آن باشد. 4- ممکن است M و N نشاندهنده انسان‌ها باشند و علامت + نیز می‌تواند نشان دهنده این باشد که اولی برادر دومی است. 5- ممکن است M و N نشان دهنده کشورها باشد و علامت + نیز می‌تواند نشان دهنده این باشد که اولی به جنگ دومی رفته.

بطور خلاصه، در نیمه اول قرن نوزدهم جبر داشت وابستگی خودش از دنیای اعداد را از دست می‌داد. چه چیزی محرک این روند بود؟ و چرا این موضوعات بیشتر از سوی ریاضیدانان بریتانیایی مطرح می‌شدند؟

10.2

همانطور که قرن هجدهم جلو می‌رفت، ریاضیات بریتانیا در حال درجا زدن بود و از بقیه پیشرفت‌های اروپا عقب افتاده بود. بخشی از آن به خاطر سِر آیزک نیوتون (Sir Isaac Newton) بود، به عبارتی، نتیجه فرعی عزتِ نفس بیش از حد بریتانیایی‌ها به خودشان، و نیوتون که قهرمان ملی آنها بود. طبق قوانین نیوتون، این عزتِ نفس بیش‌ از حد، یک واکنش معکوس و مساوی را در بر داشت. ملل بزرگ اروپایی نیز در مقابل نیوتون قهرمانانِ فرهنگی خودشان را مطرح کردند. مثلاً برای فرانسوی‌ها، دکارت همین نقش را پیدا کرد.

در واقع آلمانی‌ها دو نماد ضد-نیوتونی داشتند، که بطور وضوح یکی از آنها لایب‌نیتز و دیگری شاعر و دانشمند آنها، گُوته (Goethe)، بود. گوته از نظریه‌های نیوتون درمورد نور به شدت انتقاد می‌کرد. هنوز هم خانه گوته در شهر ویمار با رنگین‌کمانی آذین شده که نمادی ضد-نیوتونی محسوب می‌شود.

همه اینها برای ریاضیات بریتانیا مایه بدبختی بود، زیرا نمادگذاری‌هایی که نیوتون برای عملیات حسابان ابداع کرد، بطور قطع پایین‌تر از آن مواردی بود که توسط لایب‌نیتز رواج داده شدند و بعداً بقیه ریاضیدانان در سراسر اروپا از آن استفاده کردند. در حالی که لایب‌نیتز برای نمایش دیفرانسیل از dها استفاده می‌کرد، بریتانیایی‌های وطن پرست به نمادگذاری ”نقطه‌ای“ نیوتون چسبیده بودند، و مثلاً بجای اینکه بنویسند

آن را بصورت می‌نوشتند. این بر روی حسابان بریتانیایی تاثیری منفی داشت و باعث عقب افتادن و منزوی شدن آن گشت. خواندن کتاب‌ها و مقالات بریتانیایی‌ها برای ریاضیدانان اروپایی کاری خسته کننده و مبهم بود. ولی در نمادگذاری لایب‌نیتز بر روی x، که تابعی از t است، توسط عملگری مثل زیر عمل می‌شود.

و این می‌تواند جدا شده و بصورت مستقل بعنوان یک شیء ریاضی در نظر گرفته شود.

اعداد مختلط مدتها بود در ریاضیاتِ اروپا جا افتاده بودند. ولی در بریتانیا حتی اعداد منفی هنوز توسط برخی از ریاضیدانان مورد تمسخر قرار می‌گرفتند. مثلاً در کتاب اصول جبر نوشته ویلیام فرِند چنین آمده:

عدد مفروضی که از عدد دیگری کوچکتر است را می‌توان از عدد بزرگتر کم کرد، ولی کم کردن عدد بزرگتر از عدد کوچکتر مسخره است. ولی با اینحال چنین کاری توسط جبردانانی که از اعداد کمتر از هیچ [اعداد منفی] صحبت می‌کنند انجام می‌شود؛ آنها می‌گویند حاصل ضرب یک عدد منفی در یک عدد منفی، عددی مثبت است ... همه اینها سخنانی بی‌معنی هستند که عقل سلیم آنها را پس می‌زند. ولی هنگامی که مثل خیلی از سخنان جعلی دیگر آنها را بپذیریم، در میان کسانی که از تفکر جدی متنفرند، طرفداران فراوانی را پیدا می‌کند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

موضوعات ریاضی

نظریه میدان‌ها

/27/06/1401

1

”میدان“ و ”گروه“ نام دو شیء ریاضی هستند که در طول قرن 19، و طی یک سری از مراحل کشف شدند.

تا آنجایی که به ساختار داخلی آن مربوط است، یک میدان (field) پیچیده‌تر از یک گروه (group) است. به همین دلیل، معمولاً در کتاب‌های درسیِ جبر ابتدا گروه‌ها و سپس میدان‌ها معرفی می‌شوند. بااینحال حسی وجود دارد که می‌گوید یک میدان نسبت به یک گروه چیز ساده‌تری است و بنابراین می‌توان آن را آسانتر درک کرد. با اینکه گروه‌ها از لحاظ ساختاری ساده‌ترند، ولی از نظر جبردانان نسبت به میدان‌ها کاربردهای گسترده‌تری دارند.

به همین دلایل، و همینطور به منظور قابل‌پذیرش‌ بودن کشفیات گالوآ، پیش از پرداختن به نظریه گروه‌ها که در فصل‌های آتی این کتاب آنها را بررسی خواهیم کرد، ابتدا قصد دارم در این فصل به توضیح میدان‌ها بپردازم.

2

یک میدان دستگاهی از اعداد، یا چیزهای دیگری است (ولی فعلاً اعداد برای منظور ما کفایت می‌کنند) که شما می‌توانید عملیات جمع، تفریق، ضرب، و تقسیم را در آن انجام دهید. مهم نیست که شما چه تعداد از چهار عمل اصلی را انجام می‌دهید، مهم این است که حاصل آن همیشه عددی باشد که در آن میدان قرار دارد. به خاطر همین است که من گفتم میدان چیز ساده‌ای است. هنگامی که در یک میدان هستید، شما چهار عمل اصلی +، -، ×، ÷ را انجام می‌دهید. اگر شما برای مفهوم جبری یک میدان نمونه ساده‌ای را می‌خواهید، کافیست یک ماشین‌حساب جیبی ساده را در نظر بگیرید، که چهار کلید برای عملیات اصلی +، -، ×، ÷ روی آن قرار دارد.

قواعد خاصی هستند که باید از آنها پیروی شود، که هیچکدام از آنها تعجب برانگیز نیست. من قبلاً به قاعده بسته بودن اشاره کردم: نتیجه عملیات حسابی باید در خود آن میدان باشد. قاعده دیگر این است که شما چیزی شبیه ”صفر“، یا عضو خنثی، داشته باشید که وقتی آن را با عدد دیگری جمع کنید، حاصلش خودِ عدد باشد. همچنین عضو دیگری مثل ”یک“ داشته باشید که اگر آن را در عدد دیگری ضرب کنید، حاصلش خودِ عدد باشد. همچنین قواعد اصلی جبر نیز باید برقرار باشد،برای مثال، a×(b+c) همیشه با a×b+a×c مساوی باشد. هم جمع و هم ضرب باید جابجایی پذیر باشند؛ ما در میدان‌ها چیزی بنام جابجایی‌ناپذیری نداریم. بنابراین کواترنیون‌های همیلتون یک میدان را تشکیل نمی‌دهند، و فقط یک ”جبر تقسیمی“ (division algebra) هستند.

نه ℕ و نه $ℤ$ هیچکدام میدان نیستند، زیرا تقسیم دو عدد صحیح ممکن است یک عدد کسری باشد که در این دو دستگاه وجود نداشته باشد. ولی خانواده اعداد گویا، یعنی ℚ، یک میدان را تشکیل می‌دهد. شما می‌توانید در این میدان عملیات جمع، تفریق، ضرب، و تقسیم را انجام دهید و حاصل آن همیشه در ℚ باقی خواهد ماند، بنابراین ℚ یک میدان است. حسی هست که می‌گوید ℚ مهمترین و پایه‌ای‌ترین میدان است. اعداد حقیقی ℝ نیز یک میدان تشکیل می‌دهند. این در مورد اعداد مختلط ℂ نیز صدق می‌کند. بنابراین ما از قبل سه میدان ℚ، ℝ، و ℂ را داریم تا توجه خودمان را روی آنها متمرکز کنیم.

آیا در کنار ℚ، ℝ، و ℂ میدان‌های دیگری نیز وجود دارند؟ قطعاً میدان‌های دیگری نیز وجود دارند. من دو گونه متداول از آنها را توضیح می‌دهم. سپس این دو گونه را در کنار هم قرار می‌دهم تا به نظریه گالوآ و نظریه‌ گروه‌ها برسم. پس از آن به طور گذرا، به گونه سوم و مهمی از میدان‌ها اشاره خواهم کرد.

3

به غیر از میدان‌های متداول ℚ، ℝ، و ℂ، گونه دیگری از آنها هستند که میدان‌های متناهی نامیده می‌شوند. میدان‌های ℚ، ℝ، و ℂ تعداد بی‌نهایتی عضو دارند، زیرا تعداد بی‌نهایتی از اعداد گویا، اعداد حقیقی، و اعداد مختلط وجود دارند.

اینجا میدانی را معرفی می‌کنم که تنها سه عضو در آن هست، و برای راحتی کار، من آنها را 0، 1، و 2 می‌نامم. ولی اگر فکر می‌کنید استفاده از این سه علامت باعث می‌شود آنها را با اعداد صحیح معمولی که به همین شکل نوشته می‌شوند اشتباه بگیرید، شما آزاد هستید آنها را با هر علامت دیگری که می‌خواهید جایگزین کنید. مثلاً برای 0 از ”Z“ ، برای 1 از ”I“، و برای 2 از ”T“ استفاده کنید. در این میدانِ خاص، اینطور نیست که ما 2+2=4 را داشته باشیم. در اینجا 2+2=1 است. در واقع جدول جمع و ضرب کامل این میدان، که F₃ نامیده می‌شود، را در زیر می‌بینید.

شکل 1: میدان F₃.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 11

مبارزه تن به تن در سپیده دم

/1/07/1401

11.1

اجازه دهید صریح بگویم، ریاضیات موضوع خشکی است که در آن از زرق و برق‌ها یا داستان‌های عاشقانه زیاد خبری نیست. به همین دلیل داستان اواریست گالوآ (Évariste Galois) یک مورد استثناء است که توجه تاریخ‌نگاران ریاضی را بیش از اندازه به خودش جلب کرده.

ولی شاید در این مورد زیاد از حد اغراق شده. تا آن اندازه که بر ما معلوم است، حقایق مربوط به زندگی گالوآ با ابرهایی از افسانه، خطا، گمانی زنی، و موضوعات کم اهمیت پوشیده شده‌اند.

نمونه معروف آن در زبان انگلیسی، کتاب رِجال ریاضیات[5] نوشته اریک تمپل بِل است، و به غلط، داستان مُشتی ابله را حکایت می‌کند که در تعقیب یک ریاضیدان نابغه و آرمان‌‌گرا هستند، ریاضیدانی که آخرین شب زندگی خودش را صرف نوشتن کاغذهایی کرد که اساس نظریه گروه‌ها را بنا نهاد. جزئیاتِ داستانی که تمپل بِل حکایت می‌کند، و شخصیتی که از گالوآ ارائه می‌دهد نیز احتمالاً دروغ است.

در سال 1997 تام پتسینیس (Tom Petsinis) کتابی بنام ریاضیدان فرانسوی نوشت که گرچه سبک آن را نمی‌پسندم و به نظر من پایان آن نیز غیر-محتمل است، اما حقایقی را در مورد گالوآ مطرح می‌کند که محتمل‌تر هستند. بهترین منبعی که برای اینمورد سراغ دارم، وب سایتی است که توسط کیهان‌شناس و ریاضیدان آمریکایی تونی روثمن (Tony Rothman) فراهم آمده و تقریباً تمام منابع را بصوت عادلانه‌ای بررسی کرده.

گالوآ در حالی که تنها 20 سال و 7 ماه داشت طی یک نبرد تن به تن کشته شد. این نبرد تن به تن (دوئل) با تپانچه انجام گرفت، که طبق رسوم معمول، در صبح زود اتفاق می‌افتاد. ظاهراً گالوآ که مطمئن بود در آن نبرد کشته می‌شود (و شاید خودش هم همین را آرزو می‌کرد)، شب قبل از آن چند نامه نوشت. برخی از آن نامه‌ها خطاب به دوستان سیاسی‌اش بود که مانند خودش جمهوری‌خواهِ ضدسلطنت بودند. یکی از این نامه‌ها نیز خطاب به دوستش آگوست شِوالیه بود که به کارهای ریاضی او مربوط بودند.

دلیل این نبرد روشن نیست. دلیل آن می‌تواند سیاسی یا عاشقانه، یا هر دو باشد. گالوآ در یکی از نامه‌هایش نوشته بود ”من توسط دو میهن‌پرست تحریک شدم ...“. ولی در نامه دیگری می‌گوید ”من قربانی یک زنِ بدنامِ عشوه‌گر شدم ...“ گالوآ در حوالی سال 1830 در پاریس درگیر فعالیت‌های جمهوری‌خواهانه-افراطی شده بود (همان خیزشی که در کتاب بینوایان ویکتور هوگو ترسیم شده بود) او همچنین از یک عشق یک‌طرفه رنج می‌کشید.

مطمئناً این یک داستانه عاشقانه بود. همانطور که در چنین مواردی اتفاق می‌افتاد، با نگاه دقیقتری به شرایط نشان می‌دهد که مسائل عاشقانه جای خودشان را به چیزهای دیگری می‌دهند. داستان گالوآ قطعاً داستان غم‌انگیزی است، و این حقیقت که شخصیتِ عجیب او موجب بدبختی‌های او بوده، از غم‌انگیز بودن داستان او نمی‌کاهد.

11.2

در سال‌های 1830، فرانسه ملت خوشبختی نبود. پس از مرگ ناپلئون، شارل دهم پادشاه فرانسه از خاندان بوربون، توسط هم‌پیمانان خودش به سلطنت رسید. او مردی قدیمی و مرتجع بود. از سوی دیگر، شهرنشینی و صنعتی‌شدنِ سریع، بیشتر محلات پاریس را به مکان وحشتناکی برای زندگی تبدیل کرده بود، جایی که در آن صدها هزار نفر در فقر و گرسنگی به سر می‌بردند. این همان پاریسی بود که در کتابهای بالزاک و ویکتور هوگو ترسیم شده بود، جایی که یک طبقه مادی‌گرای سرمایه‌دار در کنار طبقات فقیر زندگی می‌کردند.

در 1830 فرانسه دچار یک بحران اقتصادی نیز بود. قیمت نان بسیار گران بود، و بیش از 60000 پاریسی بیکار بودند. در ماه جولای آن سال، در خیابان‌ها سنگر بپا شد، مردم کنترل شهر را بدست گرفتند، و شارل دهم مجبور شد از کشور فرار کند. یکی از شاهزادگانِ دورِ خاندانِ بوربون، بنام لویی فیلیپ، توسط معاونان مجلس بعنوان شاه جدید برگزیده شد، و به ”شاه جولای“ معروف گشت. لویی فیلیپ مردی محجوب و آزادیخواه بود. دهه 1830 با خیزش‌های مختلفی همراه بود، از جمله یک خیزش عمده در 1831 در پاریس. در طول این دهه، انتظار می‌رفت مردانِ جوانِ آتشی مزاج، که عقاید متعصبانه‌ای داشتد، تحت نظر پلیس قرار بگیرند و شاید مدت کوتاهی نیز زندانی شوند.

اواریست گالوآ (1832-1811)

11.3

اواریست گالوآ (Évariste Galois) در سال 1811 در شهر کوچکی در حومه پاریس بدنیا آمد. پدر گالوآ یک آزادی‌خواه، یک ضد روحانی، و یک ضدسلطنت بود. او در 1815 در واپسین روزهایی که ناپلئون امپراتور فرانسه بود، بعنوان شهردار برگزیده شد. پس از اینکه سلطنت دوباره احیا شد، با اینکه پدرِ گالوآ دل خوشی از سلطنت طلبان نداشت، ولی برای اینکه یکی از آنها جای او را نگیرد، به خاندان بوربون سوگند وفاداری ادا کرد.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 12

بانوی حلقه‌ها

/17/07/1401

12.1

یک گروه تنها از طریق سه اصلِ‌موضوعه تعریف می‌شود: بسته بودن، شرکت‌پذیری، داشتن عضو همانی، و داشتن عضو وارون (به بخش 11.4 رجوع کنید). این سادگی موجب می‌شود گروه‌ها حوزه وسیعی داشته باشند. این درست مانند این است که بجای اینکه بطور دقیقی از دسته‌ای از جانوران یاد کنیم، و مثلاً بگوییم ”جانورِ چهار-پا که عاج و خرطوم دارد“، خیلی کلی‌تر بگوییم ”موجود چهار-پا“. همین خصوصیتِ بسیار ساده تعریفِ گروه‌ها است که اجازه می‌دهد محدوده بکارگیری آنها خیلی فراتر از اعداد برود و چیزهای بسیاری را دربرگیرد. این همچنین نوعی آزادی عمل به گروه‌ها می‌دهد تا ساختارهای پیچیده و جالبی را داشته باشند، که گروه نرمال یکی از مفاهیم اصلی آن است.

یک میدان (به بخش ریاضی مربوط به نظریه میدان‌ها رجوع کنید) شیء پیچیده‌تری است، که برای تعریف آن به 10 اصل نیاز است. یک میدان بجای اینکه تنها به یک عمل اساسی برای ترکیب اعضای خودش نیاز داشته باشد، به دو عمل نیاز دارد: جمع و ضرب. در واقع تفریق و تقسیم فقط معکوس جمع و ضرب هستند: 8-3 یعنی 8+(-3). این پیچیدگیِ بیشتر باعث می‌شود مفهومِ ”میدان“ بیشتر به اعداد معمولی گره بخورد تا اشیاء دیگر. همچنین یک میدان بطور متناقصی ساختار درونی محدودی دارد که آن را کمتر جالب می‌کند.

شیء ریاضی دیگری هست که در جبرِ جدید خیلی مورد مطالعه قرار گرفته، و آن حلقه (ring) است. یک حلقه نسبت به گروه پیچیده‌تر، ولی نسبت به یک میدان ساده‌تر است، بنابراین هرچند کاربرد آن به اندازه گروه‌ها گسترده نیست، ولی می‌تواند از حوزه اعداد معمولی جلوتر رود و کاربردهای گسترده‌تری داشته باشد. مانند یک گروه، حلقه نیز می‌تواند ساختارهای درونی جالبی داشته باشد. مفهوم اساسی که در حلقه‌ها مطرح است، ایدآل (ideal) بودن آنها است. من این مفهوم را در طول این فصل و فصل بعدی توضیح خواهم داد.

اغلب اوقات مفهوم حلقه بهترین چیزهای هر دو دنیا، یعنی میدانها و گروه‌ها، را به ریاضیدانان می‌دهد. مثلاً، حلقه‌ها در مرکز هندسه جبریِ نوین قرار دارند، که منبع عمیق‌ترین و چالش‌برانگیزترین ایده‌ها در جبر نوین است. ولی بطور غیرمعمولی، زمان زیادی طول کشید تا بطور کامل به قدرت حلقه‌ها پی برده شود.

گفته می‌شود که نظریه حلقه‌ها با آخرین قضیه فرما شروع شد. البته معلوم شده که این خیلی درست نیست. با اینحال آخرین قضیه فرما نقطه شروع خوبی برای توضیح حلقه‌ها است، و من هم با شرح همین موضوع کارم ادامه می‌دهم.

12.2

من قبلاً در بخش 2.6 به آخرین قضیه فرما اشاره کردم، و گفتم در حوالی سال 1637 فرما در حاشیه کتاب حساب دیافانتوس، قضیه خودش را به این صورت بیان کرد و گفت معادله

xⁿ+yⁿ = zⁿ

برای اعداد صحیح x,y,z و n، هنگامی که n بزرگتر از 2 باشد هیچ جوابی ندارد. خود فرما در 1659 اثباتی را برای n=4 طرح کرد، که بعداً گاوس اثبات کامل آن را ارائه داد. اویلر در 1753 اثباتی را برای n=3 ارائه داد.

برای مدت نیم قرن هیچ پیشرفت محسوسی درباره این موضوع صورت نگرفت، تا اینکه سوفی ژرمن (Sophie Germain)، که یکی از سه ریاضیدانِ زنِ بزرگ است که در کتاب حاضر به آنها اشاره شده، اثبات کرد که قضیه فرما برای دسته بزرگی از اعداد صحیح x,y,z و n درست است. توضیح اینکه بگوییم چه دسته‌های چهارتایی از اعداد صحیح در این دسته جا می‌گیرند از حوصله این کتاب خارج است. ولی همینقدر کافی است که بگوییم قدم‌های بعدی در پیشرفت این قضیه، بر روی نتایجی بنا شد که سوفی ژرمن حاصل کرده بود.

سوفی ژرمن (1831-1776)

در 1825، ریاضیدان فرانسوی آدرین-ماری لژاندر (Adrien-Marie Legendre)، که در آن زمان 72 ساله بود، و ریاضیدان آلمانی لوژون دریکله (Dirichlet Lejeune) بطور جداگانه حالت n=5 را اثبات کردند. تا آن موقع همه فهمیده بودند که چالش واقعی این است که قضیه برای حالت‌هایی اثبات شود که در آنها n یک عدد اول باشد، بنابراین قدم بعدی اثبات n=7 بود. در 1839، ریاضیدان فرانسوی دیگری بنام گابریل لامه (Gabriel Lamé)، این را اثبات کرد. ولی در آن زمان، داستان چرخش جدیدی پیدا کرد.

12.3

فقط یادآوری می‌کنم که مجموعه $ℤ$ ، یعنی مجموعه اعداد صحیح، حاوی کلیه اعداد صحیح مثبت، اعداد صحیح منفی، و صفر است.

$ℤ$ : …,…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, . . .

(این فهرست هم از سمت چپ، و هم از سمت راست تا بی‌نهایت ادامه دارد.) تا اینجا $ℤ$ یک میدان نیست.شما در $ℤ$ می‌توانید آزادانه جمع و ضرب کنید، و جوابی که حاصل می‌کنید هنوز در $ℤ$ قرار دارد. ولی تقسیم فقط برخی از مواقع جواب می‌دهد. اگر شما -12 را بر 4 تقسیم کنید، جواب در $ℤ$ است. ولی اگر -12 را بر 7 تقسیم کنید، جواب در $ℤ$ نیست. بنابراین، بدلیل اینکه شما نمی‌توانید آزادانه بدون اینکه از $ℤ$ خارج شوید عملِ تقسیم را انجام دهید، پس $ℤ$ یک میدان نیست.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

موضوعات ریاضی،

هندسه جبری

/25/07/1401

1

همانطور که در فصل بعد توضیح خواهم داد، هندسه تاثیر بسیار مهمی بر جبر مُدرن برجا گذاشته. سعی من بر این است که سیرِ سرشت و رشد این تاثیر را دنبال کنم. در اینجا فقط می‌خواهم تعدادی از ایده‌های اساسی در مورد هندسه جبری (algebraic geometry) را معرفی کنم. به عنوان مقدمه‌ای برای این موضوع، از یک مبحث قدیمی و خوب ریاضی، بنام مقاطع مخروطی استفاده می‌کنم.

2

مقاطع مخروطی (Conic sections)، که غالباً از آنها فقط به عنوان مخروط‌ها نام برده می‌شود، دسته‌ای از منحنی‌های ساده هستند، همان‌هایی که وقتی یک صفحه از یک مخروطِ دایره‌ای عبور می‌کند، حاصل می‌شوند (نکته مهمی که باید به آن توجه کنید این است که مخروط مورد نظر راس و پایه خاصی ندارد و از هر دو طرف تا بینهایت امتداد دارد). در شکل 1، صفحه‌ قطع کننده، صفحه همین کتاب است، که باید تصور کنید صفحه شفافی است. راس مخروط در پشت این صفحه است. در اولین تصویر، محور مخروط با صفحه زاویه قائمه تشکیل داده، بنابراین مقطع حاصله یک دایره است. سپس من کمی مخروط را کج کرده‌ام. در اینحالت دایره به یک بیضی تبدیل شده. سپس همانطور که مخروط را بیشتر کج کرده‌ام، یک سمت از بیضی ”به بی‌نهایت رفته“، و یک سهمی (parabola) حاصل شده. کج کردن بیشتر مخروط، یک منحنی دو قسمتی بنام هذلولی (hyperbola) را به ما می‌دهد.

شکل 1: مقاطع مخروطی که از قطع کردن یک مخروط توسط این صفحه حاصل شده‌اند.

البته همه اینها به هندسه مربوط است. برای اینکه به جبر برسیم، ما از دکارت پیروی می‌کنیم. آن بی‌نهایت نقطه‌ای که یک منحنی را می‌سازند، و ما مختصات آنها را x و y می‌نامیم، در یک معادله درجه دوم بر حسب x و y صدق می‌کنند:

ax²+2hxy+by²+2gx+2fy+c=0

نامیدن این ضرایب به عنوان a, h, b, g, f, c ، ممکن است کمی عجیب بنظر برسد، ولی من بعداً دلیل آن را توضیح خواهم داد. راه دیگری که می‌توان مقاطع مخروطی را بیان کرد این است: یک مقطع مخروطی عبارت است از مجموعه جواب‌های یک چندجمله‌ای درجه دوم که دو مجهول دارد. این مجموعه جواب‌ها بصورت (x,y) هستند و مقدار چندجمله‌ای را صفر می‌کنند.

برای مثال بیضی که در شکل 2a نشان داده شده، دارای معادله زیر است:

153x²-192xy+97y²+120x-590y+1600=0

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 13

بازگشت دوباره هندسه

/29/07/1401

13.1

در دفاتر اکثر گروه‌های ریاضی دانشگاه‌های جهان، مجموعه‌ای از مدل‌های ریاضی قرار دارند که در پشت ویترین‌های شیشه‌ای خاک می‌خورند. آنها معمولاً شامل چندوجهی‌های محدب و ستاره‌ای که با ریسمان درست شده‌اند، توپ‌های پینگ-پونگ که با چسب به هم متصل شده‌اند تا روش‌های مختلف چیدن کُره‌ها را نمایش دهند، یک نوار موبیوس، و شاید هم یک بطری کلاین، و اشیاء عجیب دیگر هستند.

شکل 1-13: چند وجهی‌های محدب (چپ)، ستاره‌ای (راست).

امروزه چنین مدل‌های ارزش سابق خودشان را ندارند. با ظهور نرم‌افزارهای ترسیم گرافیکی، مانند مِیپِل (Maple) و مَتِمتیکا (Mathematica)، که در یک لحظه می‌توانند این اشکال را روی صفحه کامپیوتر رسم کرده و هر طور که کاربر می‌خواهد، آنها را دوران، انتقال، و تغییر شکل دهند، حالا دیگر ساخت چنین اشیائی از چوب،کاغذ، مقوا، و ریسمان کار پردردسر و بی‌موردی محسوب می‌شود. ولی برای ریاضیدانان و دانشجویان ریاضی در قرون 19 و 20 ساختن مدل‌های فیزیکی از اشیاء هندسی سرگرمی پرطرفداری بود، و من افسوس می‌خورم که حالا چنین کارهایی کمتر انجام می‌شود. من در دوره نوجوانی خودم در دهه 1950، ساعات خوش زیادی را صرف اینکار کردم. چیزی که به آن افتخار می‌کردم، ساختن یک مدل مقوایی از پنج مکعب بود که در یک دوازده‌وجهی محاط شده بودند، و همه مکعب‌ها رنگ متفاوتی داشتند.

علاقه‌ای که نسبت به ساخت ابزارهای بصری و مدل‌های ریاضی وجود داشت، یکی از پی‌آمدهای تولد دوباره هندسه در اوایل قرن 19 بود. همانطور که در بخش 10.1 اشاره کردم، باوجود اینکه در قرن 17 پیشرفت‌های مهمی در هندسه حاصل شده بود، ولی تحت‌الشعاع ایده‌هایی قرار داشت که از طریق حسابان مطرح شده بودند. تا سال 1800، هندسه دیگر آن رشته جذاب ریاضی نبود که قبلاً بود، و شما می‌توانستید یک ریاضیدان حرفه‌ای محترمی باشید که به غیر از اصول هندسه اقلیدسی، که خواه ناخواه آن را در مدرسه یادگرفته‌اید، چیز زیادی دراینباره نمی‌دانست. ولی در نسل بعدی اوضاع تغییر کرد.

13.2

اولین پیشرفتی که در هندسه قرن نوزدهم رخ داد، از سوی ریاضیدان فرانسوی ژان-ویکتور پونسله (Jean-Victor Poncelet) صورت گرفت. پونسله در سن 24 سالگی بعنوان یک افسر مهندس به همراه ارتش ناپلئون به روسیه اعزام شد. او به سختی خودش را به مُسکو رساند. در عقب نشینی که در زمستانِ وحشتناک آن سال صورت گرفت، پس از نبرد کراسنوی، او به حال خودش رها شد تا بمیرد. یک دسته تجسسی روسی او را دستگیر و برای بازجویی به پایگاه فرستاد. پونسله که حالا یک اسیر جنگی بود باید به مدت پنج ماه در جلگه‌های یخ زده راه‌پیمایی می‌کرد تا به اردوگاه ساراتوف در ولگا برسد.

پونسله برای اینکه حواس خودش را از سختی‌های زندان پرت کند، تمرکزش را روی آموزش‌های ریاضی خوبش گذاشت که در زمان تحصیل در مدرسه پلی‌تکنیک پاریس آنها را کسب کرده بود. زمانی که در سپتامبر 1814 به او اجازه داده شد به فرانسه بازگردد، او هفت دفترچه با خودش داشت که پر از یادداشت‌های ریاضی او بود. این یادداشت‌ها بعداً پایه‌ای شد برای کتاب رساله‌ای در باب خواص افکنشی اشکال، یعنی پایه هندسه تصویری نوین.

کتاب پونسله خیلی جنبه جبری نداشت. در واقع این کتاب طرفدار یکی از بحث‌هایی بود که در نیمه اول قرن 19 در جریان بود، یعنی مشاجره میان هندسه تحلیلی (analytic) و ترکیبی (synthetic). هندسه تحلیلی که از دکارت به ارث رسیده بود، از تمام قدرت جبر و حسابان استفاده می‌کرد تا نتایجی را در مورد اشکال هندسی (خطوط راست، مقاطع مخروطی، منحنی‌ها و سطوح پیچیده‌تر) حاصل کند. از سوی دیگر هندسه ترکیبی که از یونانیان و از طریق پاسکال به ارث رسیده بود، برهان‌های منطقی خالص را ترجیح می‌داد، همان‌هایی که تا حد ممکن از اعداد و جبر کمتر استفاده می‌کردند.

بدلیل اینکه در قضیه‌‌های مربوط به هندسه تصویری اشاره‌‌ای به فواصل یا زوایا نمی‌شود، در نگاه اول این هندسه شبیه هندسه ترکیبی بنظر می‌رسد، که پس از دو صده از بازی با اعداد در هندسه تحلیلی ظهور کرده. بعداً در 1820 ریاضیدان آلمانی آگوست موبیوس، کارل فوئرباخ، جولیوس پلوکر، بطور مستقل از یکدیگر، با آوردن مختصات متجانس به هندسه تصویری، اجازه دادند این هندسه بصورت جبری درآید.

علاوه بر کارهای پونسله در جهت پایه‌گذاری هندسه تصویری نوین، در دهه 1820 انقلاب دیگری نیز در هندسه درحال وقوع بود، و آن انتشار مقاله نیکلای لوباچِفسکی درباره هندسه‌‌ نااقلیدسی در یک نشریه محلی روسی بود. او بعداً همین مقاله را به آکادمی علوم سنت پترزبورگ ارائه داد، ولی آنها به دلیل آهانت‌‌آمیز بودن محتوایش، این مقاله را رد کردند! لوباچِفسکی استدلال کرده بود که برخی از فرض‌‌های هندسه کلاسیک (مثل اینکه مجموع زوایای یک مثلث همیشه برابر 180 درجه است) را نمی‌‌توان به عنوان حقایق عمومی مسلم پنداشت، ولی می‌‌توان آنها را بعنوان یک سری اصولِ موضوعه اختیاری در نظر گرفت. با اختیار کردن اصولِ موضوعه متفاوت، ممکن است شما به هندسه متفاوتی برسید، هندسه‌‌هایی که هیچ شباهتی به هندسی اقلیدسی ندارند، و اینها همان هندسه‌‌های نااقلیدسی (non-Euclidean geometry) هستند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 14

حوزه‌های مختلفِ جبری

/11/08/1401

14.1

از حدود سالهای 1870 به بعد، برنامه ارلانگنِ کلاین به واقعه مهمی تبدیل شد، و درک جدیدی از جبر پدید آمد که بر روی کل ریاضیات تاثیر گذاشت. اشیاء جدیدِ جبری (ماتریس‌ها، جبرها، گروه‌ها، چندگوناها، و غیره) که در قرن نوزدهم توسط جبردانانِ آن دوره کشف شده بودند، کم‌کم توسط ریاضیدانان حوزه‌های مختلف (هندسه، توپولوژی، نظریه اعداد، نظریه توابع، و غیره) بعنوان ابزارهای قابل اتکا بکار گرفته می‌شدند. تا آنجا که به هندسه مربوط بود من در فصل 13 تلاش کردم این جبری‌سازیِ فراگیر را توضیح دهم. در اینجا قصد دارم این را به توپولوژی جبری، نظریه جبری اعداد، و برخی پیشرفتهایی که از اواخر قرن نوزدهم تا اواسط قرن بیستم در حوزه هندسه جبری روی داد، گسترش دهم.

14.2

ابتدا با توپولوژی جبری (Algebraic Topology) شروع می‌کنم. همانطور که در بخش ریاضی مربوط به هندسه جبری گفتم، توپولوژی در ابتدا بعنوان ”هندسه سطوح لاستیکی“ مطرح شد. یک سطح دو-بعدی (مثلاً سطح یک کره) را در نظر بگیرید که از ماده‌ای ساخته شده که بسیار قابل اتساع است. از نظر یک متخصص توپولوژی، هر سطحی که سطح کره بتواند با کشیدن یا فشردن به آن تبدیل شود، با سطح کره ”یکسان است“. البته احتیاط‌هایی باید انجام شود تا از لحاظ ریاضی توپولوژی دقیق باشد. شما در مورد برش، یا چسباندن یک ناحیه متناهی به یک نقطه بدون‌بعد، یا اجازه دادن سطح برای عبور از خودش، به قواعدی نیاز دارید که در کاربردهای مختلف کمی با هم فرق دارند. ولی تعریف گسترده متعارف در اینجا کفایت می‌کند.

در واقع تا اواخر قرن نوزدهم توپولوژی ارتباط چندانی با جبر نداشت. توسعه آن هم بسیار کند بود. لغت ”توپولوژی“ برای اولین بار در دهه 1840 توسط ریاضیدان آلمانی یوهان لیستینگ (Johann Listing) بکارگرفته شد. بنظر می‌رسد که بسیاری از ایده‌های لیستینگ از گاوس الهام گرفته شده بود. ولی گاوس هیچ وقت مطلبی درباره توپولوژی منتشر نکرد. لیستینگ در 1861 سطحی را شرح داد که ما امروزه آن را بعنوان نوار موبیوس (Möbius strip) می‌شناسیم (شکل 1-14). خود موبیوس 4 سال بعد این سطح را معرفی کرد، و بنا به دلایلی، ارائه او بود که توجه ریاضیدانان را جلب کرد.

شکل 1-14: یک نوار لیستینگ (نوار موبیوس).

استفاده برنهارد ریمان از سطوح خود-متقاطع برای درک توابع، که در رساله دکترای خودش آنها را مطرح کرده بود، عامل دیگری برای توسعه ایده‌های توپولوژیک بود. کامیل جُردن با مطالعه دقیق این سطوح ریمانی به این ایده‌ رسید که ببیند بر سر حلقه‌های بسته‌ای که در داخل آنها جا می‌گیرند، چه اتفاقی می‌افتاد (البته در اینجا منظور من از لغت ”سطوح“، جانشینی برای ”فضاها“ است که به این طریق می‌توان آنها را آسانتر تصور کرد).

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 15

از حسابِ عام تا جبرِ عام

/17/08/1401

15.1

بعنوان یک نگاه اجمالی به کارهایی که در دهه‌های اخیر در زمینه جبر انجام شده، در زیر بخشی از فهرست جوایز فرانک نلسون کول، که توسط انجمن ریاضی آمریکا اهدا می‌شود آمده. (فهرست کامل بر روی اینترنت موجود است).

1960: به Serge Lang اهداء شد، بخاطر مقاله او تحت عنوان ”نظریه میدان کلاس غیرمنشعب روی میدان‌های تابع چند متغیره“، و به Maxwell A. Rosenlicht برای مقاله‌اش درباره تعمیم چندگوناهای یاکوبی ...

1965: به Walter Feit و John G. Thompson اهداء شد، بخاطر مقاله مشترکشان با عنوان ”حل‌پذیری گروه‌ها از مرتبه فرد“...

2000: به Andrei Suslin اهداء شد، برای کارهایش در زمینه (motivitic cohomology)

2003: به Hiraku Nakajima اهداء شد، بخاطر کارهایش روی نظریه نمایش و هندسه.

با مشاهده این فهرست خواننده این کتاب ممکن است تصور کند که من در پوشش موضوعات جبری کوتاهی کرده‌ام. ”نظریه نمایش“، ”چندگونا‌های یاکوبی“، "نظریه میدان کلاس غیرمنشعب"، نظریه ”motivitic cohomology“، اینها دیگر چه هستند؟

خوب اینها موضوعاتی مربوط به جبر نوین می‌باشند که حول محور مفاهیم اصلی مثل گروه، جبر، چندگونا، ماتریس، و غیره بنا شده‌اند، که امیدوارم توانسته باشم آنها را تا حد ممکن در بخش‌های مختلف این کتاب توضیح دهم. ولی درک اصطلاحاتی که در بالا به آنها اشاره شد، تنها یکی دو قدم با ایده‌های اساسی قرن 19 فاصله دارد. برای مثال، نظریه نمایش (Representation) به مطالعه گروه‌ها و جبرهایی می‌پردازد که توسط ماتریس‌ها مدل‌سازی می‌شوند، چیزی که من در بخش 9.6 اشاره کوتاهی به آن کردم. نظریه میدان کلاس (Class field theory) رویکردی بسیار تعمیم یافته و نوین به مسائلی است که از تجزیه‌های غیر-یکتا ناشی می‌شود، مسئله‌ای چنان پیچیده که موجب آزار کوشی و لامه شده بود و من در بخش 12.4 به آن اشاره کردم. حل‌پذیری (Solvability) به موضوع ساختار گروه‌ها ربط دارد، که یادآور حل‌پذیری معادلات چندجمله‌ای ... و غیره است.

ولی این یک واقعیت است که جبر بسیار پیچیده شده و حقیقتاً موضوعاتی نظیر motivitic cohomology”“ را نمی‌توان برای کسانی که مدرک کارشناسی ریاضی ندارند، یا حتی برای کسانی که این مدرک را دارند ولی گرایش تخصصی آنها جبر نیست، توضیح داد. جبر به حوزه‌ بسیار گسترده‌ای تبدیل شده که موضوعات متنوعی را دربر می‌گیرد (13 موضوع از 63 موضوع اصلی که توسط انجمن ریاضی آمریکا طبقه‌بندی شده به جبر مربوط هستند).

بنابراین در این مرحله من قصد دارم از حق نویسندگی خودم استفاده کنم و فقط به موضوعات و اشخاصی بپردازم که در چند دهه اخیر در جبر فعالیت کرده‌اند. البته هیچ ادعایی ندارم که این تصویر کاملی از جبرِ معاصر است. ابتدا در بخش‌های 15.2 تا 15.5 به نظریه دسته‌ها (category theory) اشار می‌کنم، سپس در بخش‌های 15.6 تا 15.9 به زندگی و کارهای الکساندر گروتندیک می‌پردازم، و در بخش‌های 15.10 و 15.11 به کاربردهای جبر نوین در فیزیک می‌پردازم. توضیح مبحث ”motivitic cohomology“ را به کتاب دیگری در آینده واگذار خواهم کرد ...

15.2

یکی از پرطرفدارترین کتاب‌های درسی برای دانشجویان دوره لیسانس در نیمه‌های قرن بیستم کتابی بود با عنوان نظری اجمالی به جبر نوین نوشته بیرکهوف (Birkhoff) و مک‌لین. این کتاب که ابتدا در 1941 منتشر شد، مفاهیم اصلی جبر جاری در نیمه‌های قرن بیستم را با روشی واضح توضیح می‌داد، که برای آماده‌سازی دانشجویان حاوی صدها تمرین نیز بود. اعداد، چندجمله‌ای‌ها، گروه‌ها، حلقه‌ها، میدان‌ها، فضاهای برداری، ماتریس‌ها، و دترمینان‌ها همه در این کتاب آمده بودند. من خودم زمانی که دانشجوی دوره لیسانس بودم جبر را با این کتاب یاد گرفتم، و مطمئن هستم که کتاب خودم هم از آن تاثیر گرفته (در واقع این تاثیر بیش از این بوده، زیرا من برای بهتر رساندن مطالب این کتاب، چند تمرین از کتاب آنها را در اینجا آوردم).

شکل 1-15: تصویری از دو کتاب بیرکهوف و مک‌لین. سمت چپ نسخه 1941، و سمت راست نسخه 1967.

در سال 1967 نسخه کاملاً جدیدی از این کتاب منتشر شد، و عنوان آن هم تنها به جبر تغییر کرده بود (تصویر سمت راست). از همه مهمتر، ارائه مطالب تغییر کرده بود. فصل چهارم کلاً جدید بود، با عنوان ”ساخت‌های عام“، که با تابع‌گرها (functors)، دسته‌ها (categories)، ریخت‌ها (morphisms)، و مجموعه‌های جزئاً مرتب (posets) سر و کار داشت. هیچ یک از این اصطلاحات در نسخه 1941 کتاب وجود نداشت. یک ضمیمه طولانی 39 صفحه‌ای نیز تحت عنوان ”فضاهای مستوی و تصویری “ به این کتاب اضافه شده بود.

اینکه یک کتاب درسی دوره کارشناسی تنها 26 سال پس از انتشارش به چنین حجم گسترده‌ای از بازبینی نیاز داشته باشد کمی شگفت‌انگیز است. چه اتفاقی افتاده بود؟ در این مدت کوتاه، این اشیاء جدید ریاضی (این تابع‌گرها و مجموعه‌های جزئاً مرتب ...) ناگهان از کجا آمده بودند؟

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

09/04/1401

[1] - DSB= Dictionary of Scientific Biography. ترجمه این کتاب تحت عنوان ”خلاصه زندگی‌نامه دانشمندان“ از سوی انتشارات علمی فرهنگی منتشر شده است (مترجم).

[2] - در این زمینه، ساعت‌، دقیقه، و ثانیه‌ ارتباطی به واحدهای اندازه گیری زمان ندارند، زیرا این لغت‌ها حدود 3000 سال بعد برای اندازه گیری زمان بکار برده شدند. در اینجا ساعت‌، دقیقه، و ثانیه‌ بخش‌های عدد 60 هستند (مترجم).

[3] - این کتاب تحت عنوان پَخستان توسط مترجم گرانمایه، آقای منوچهر انور به فارسی ترجمه شده، ولی مترجم کتاب حاضر در بکار بردن لغت ”پَخ“ بجای flat زیاد راحت نبوده، و آن را فاقد بار هندسی لغت ”تخت“ می‌داند که در اکثر کتب فنی بجای لغت flat از آن استفاده می‌شود. چندین فیلم انیمیشن نیز بر اساس این کتاب ساخته شده که خواننده علاقه‌مند می‌تواند آنها را روی اینترنت جستجو کند (مترجم).

[4] نام این دودمان با نام سرزمین چین یکسان است (مترجم).

[5] - این کتاب در سال 1348 توسط جناب آقای حسن صفاری تحت عنوان ریاضی‌دانان نامی به فارسی ترجمه شد (مترجم).

Like: ,

ترجمه‌های کامران بزرگزاد

show_banner(0);

3

6

1.3

پدر جبر

2.6

2.8

تکمیل و احیا

3.5

3

بازرگانی و رقابت

ریشه‌های واحد

2

فضاهای برداری و جبرها

جهش به بُعد چهارم

دترمینان‌ها و ماتریس‌ها

9.1

10.1

نظریه میدان‌ها

2

مبارزه تن به تن در سپیده دم

12.3

هندسه جبری

بازگشت دوباره هندسه

13.2

14.2

از حسابِ عام تا جبرِ عام

15.1

15.2