خلاصه‌ای از بخش‌های کتاب

مقدمه‌ای بسیار کوتاه درباره بی‌نهایت

نوشته یان استوارت (Ian Stewart)

  

ترجمه کامران بزرگزاد ایمانی

 

مقدمه مترجم   2

درباره این کتاب.. 2

درباره نویسنده. 2

مقدمه مؤلف... 3

رئوس مطالب کتاب.. 4

فصل 1. 5

معماها‌، اثبات‌‌ها، و پارادوکس‌ها 5

نُه مورد از جذابیت‌های بی‌نهایت.. 5

حل معماهای ذکرشده و تشریح آنها 6

فصل 2. 9

رويارویي با بی‌نهایت.. 9

متناهی و نامتناهی.. 9

فصل 3. 9

دیدگاه‌های تاریخی درباره بی‌نهایت.. 9

هشدار: مطالب زیر ممکن است حاوی بی‌نهایت باشند! 10

فصل 4. 10

جنبه‌های فرعی بی‌نهایت.. 10

اثبات قضیه ارشمیدس... 10

فصل 5. 12

بی‌نهایتِ هندسی... 12

نمای خطی (پرسپکتیو خطی) 12

فصل 6. 12

بی‌نهایتِ فیزیکی... 12

بی‌نهایت در نور شناسی.. 13

فصل 7. 13

بی‌نهایتِ شمارشی... 13

شمارش و تطبیق.. 14

 

 

 مقدمه مترجم

درباره این کتاب

موضوع کتاب حاضر درباره بی‌نهایت است. در فرهنگ نوشتاری ما واژه بی‌نهایت با واژه‌های مختلفی مثل، بی‌اندازه، بی‌کران، نامتناهی، لایتناهی، لایزال و ...  قرین است، که البته کاربرد هر یک از این واژه‌ها به زمینه و حوزه گفتار بستگی دارد. ما در فرهنگ گفتاری خودمان از لغت بی‌نهایت بیشتر بعنوان قیدی استفاده می‌کنیم تا بر بزرگی چیزی تاکید کنیم و مثلاً می‌گوییم ”فلانی بی‌نهایت پول‌دار است“، یا ”بی‌نهایت دوستت دارم“. ولی در بیشتر این موارد، ما اندازه چیزِ مورد نظر خود را درست نمی‌دانیم، ولی می‌دانیم که خیلی زیاد (یا بزرگ) است و به همین جهت، نهایتی را برای آن نمی‌بینیم. ولی آیا واقعاً استفاده از لغت بی‌نهایت برای اینها درست است؟ واضح است که چنین نیست، ولی این زبان انسان است و چون هزینه‌ای ندارد، به قول معروف به‌ آسانی می‌چرخد و برای رساندن بیان خودش از هر صفت و قیدی که می‌خواهد بهره می‌گیرد.

ولی آنچه در این کتاب بطور اجمالی مورد بررسی قرار می‌گیرد مفهوم بی‌نهایت، و آن چیزهایی است که می‌توان آنها را بی‌نهایت نامید. همانطور که در ادامه کتاب خواهید دید، بی‌نهایت مبحثی است که در حوزه‌های مختلفی مثل ریاضیات، فیزیک، فلسفه، و الهیات مطرح است، و در هر یک از آنها می‌تواند معانی مختلف، و حتی ناسازگاری، را داشته باشد.

ما معمولاً برای اشاره به چیزهایی که بسیار بزرگ هستند از لغت بی‌نهایت استفاده می‌کنیم، ولی بی‌نهایت جنبه دیگری نیز دارد و آن موضوعِ ’بی‌نهایت کوچک‌‘، یا اینفینی‌تِسیمال، است که از قرن 17 به بعد مطرح بوده و بیشتر جنبه ریاضی دارد.

از حدود 2500 سال به این سو، مبحث بی‌نهایت در فلسفه مطرح بوده، و اولین کسی که بطور جدی در این مورد سخن گفت ارسطو بود که بی‌نهایت را به دو نوع ’واقعی‘ و ’بالقوه‘ تقسیم کرد. نویسنده کتاب حاضر یک ریاضیدان است، و معلوم است که این کتاب بیشتر بر جنبه‌های ریاضی بی‌نهایت تکیه دارد، ولی در اینجا به جنبه‌های تاریخی، فلسفی، الهیاتی، منطقی، و فیزیکی بی‌نهایت نیز اشاره می‌شود.

هر یک از موارد فوق مباحث سنگینی هستند که حقیقتاً می‌توان درمورد آنها ده‌ها رساله و کتاب نوشت. ولی همانطور که از عنوان کتاب پیدا است، این فقط ’مقدمه بسیار کوتاهی‘ بر موضوع بی‌نهایت است. درصورتی که خواننده کتاب به هر یک از موضوعات مطرح شده گرایش بیشتری دارد، با مراجعه به منابعی که در پایان کتاب به آنها اشاره شده می‌تواند مطالعات خودش را گسترش دهد.

استوارت در طول 30 سال گذشته چندین کتاب درباره بی‌نهایت نوشته که کتاب حاضر آخرین و جدیدترین آنها است که در سال 2018 منتشر شده.

درباره نویسنده

این سومین کتابی است که از یان استوارت ترجمه می‌کنم. دو کتاب قبلی یکی ’چرا زیبایی واقعیت است؟‘  و دیگری ’جهان شگفت‌انگیز اعداد‘ بود. این که چرا به به آثار استوارت پرداخته‌ام دلیل ساده‌ای دارد: او در نوشتن کتابهای علمی تبحر خاصی دارد و همچنین موضوع کتابهای او شامل مواردی می‌شود که مورد علاقه مترجم نیز هست؛ مباحثی مثل ریاضیات، کیهان‌شناسی، فلسفه، و تاریخ علم. احتمالاً این کتاب نیز آخرین کتابی نخواهد بود که از این نویسنده ترجمه می‌کنم.

یان استوارت (Ian Stewart) ریاضیدان و مؤلف انگلیسی در سال 1945 در انگلستان بدنیا آمد، مدرک کارشناسی خود را در رشته ریاضی از دانشگاه کمبریج دریافت کرد، سپس در سال 1967 برای گرفتن دکترای خود به دانشگاه واریک (Warwick) رفت، و از آن پس نیز در همین دانشگاه مشغول تدریس و تحقیق بوده است.

استوارت از جمله نویسندگانی است که به ترویج دانش علمی، و بالاخص ریاضیات، شهرت دارد. از وی بیش 10 کتاب درسی، 30 کتاب عمومی غیر تخصصی، و بیش از صد و پنجاه مقاله منتشر شده. سری کتابهای (Discworld)، که او با زیست شناس مشهور جک کوهن نوشته بسیار معروف و پر فروش بوده‌اند.

کامران بزرگزاد

تابستان 1398

 

مقدمه مؤلف

اینکه انسان درباره مفهوم گسترده‌ای مثل بی‌نهایت مقدمه کوتاهی بنویسد متناقض به‌نظر می‌رسد، ولی مسئله این است که خود بی‌نهایت موضوعی متناقض است. بی‌نهایت بسیار سودمند است، و ریاضیدانان و کاربرانِ ریاضیات بدون داشتن چنین مفهومی از مسیر خودشان منحرف می‌شوند. ولی بی‌نهایت می‌تواند خطرناک نیز باشد، مگر اینکه با احتیاط فراوانی بکار گرفته شود. گرچه فیلسوفان و خداشناسان نیز با همین معضل روبرو هستند، ولی آنها به چیزهای متفاوتی تکیه می‌کنند. حدود دو هزار سال طول کشید تا انسان بتواند بی‌نهایت را بطور صحیحی بکار گیرد، ولی این موضوعی است که هنوز هم می‌تواند مشکل‌زا باشد.

اولین سابقه‌ای که برای استعمال لغت بی‌نهایت دردست است به یک فیلسوف یونانیِ پیش–سقراطی بنام آناگزي‌مندر (Anaximander) باز می‌گردد که در حدود سالهای 580 پیش از میلاد زندگی می‌کرده. لغتی که او برای این موضوع بکار می‌برد اَپِیرون (apeiron) بود که می‌توان آن را به چند صورت معنی کرد: بی‌کران، نامحدود، نامعین، بی‌نهایت. زمینه فکری او جستجو برای منشاء همه چیزها بود، و سرانجام به این نتیجه رسید که باید یک جرم اولیهِ بی‌پایان وجود داشته باشد. اَپِیرونِ پایا‌ن‌ناپذیر می‌توانست هرچیزی را بدون اینکه مورد استفاده قرار گیرد تولید کند. آنچه دقیقاً در ذهن آناگزي‌مندر می‌گذشت بر کسی معلوم نیست، ولی خیلی از محققان آن را نوعی بی‌نظمی ابتدایی می‌دانند که می‌توانست از چهار عنصر کهن، یعنی خاک، هوا، آب، و آتش، که یونانیان باستان عقیده داشتن منشاء همه چیزها هستند، سرچشمه بگیرد.

آناگزي‌مندر پیشنهاد کرد که واقعیتِ منظم از روی بی‌نظمی که خواص متضاد را تکه تکه می‌کند ایجاد شده (یا بهتر است گفته شود عصاره گرفته). از این رو در دنیای امروز، اَپِیرون شبیه توصیف مکانیک کوانتوم برای منشاء ماده از طریق پیدایش ذرات و پاد ذرات (antiparticle) است، یا شبیه پارادوکس گالیله است که می‌گفت یک مجموعه بی‌نهایت می‌تواند با یک زیرمجموعه مناسب جور شود، یا شبیه هتلِ هیلبرت است که بی‌نهایت اطاق دارد، و اگر ناگهان تعداد بی‌نهایتی مهمان سربرسند، با جابجا کردن مهمانان موجود می‌توان همه مهمانان جدید را جا داد. همه اینها را می‌توان بصورتی تفسیر کرد که چیزی از یک مجموعه بی‌نهایت استخراج شود، بدون اینکه تمام شوند. حل یک معما باعث شد تا درک ما از مفهوم بی‌نهایت عمیق‌تر شود، و آن این بود که برخی بی‌نهایت‌ها از بقیه بزرگترند، و این چیزی بود که گئورگ کانتور (Georg Cantor) به آن پی برد.

اولین اشارات شناخته شده‌ای که به مفهومِ ریاضی بی‌نهایت شده در معماهای معروف زنون ایلیایی (Zeno of Elea) دیده می‌شود. زنون نیز یک فیلسوف پیش-سقراطی بود که حوالی سالهای 490 تا 430 پیش از میلاد زندگی می‌کرده. معروفترین معمای زنون، معمای آشیل و لاک‌پشت است. لاک‌پشت و آشیل با هم مسابقه می‌دهند و با ارفاقی که در حق لاک‌پشت می‌شود، به او اجازه می‌دهند تا زودتر حرکت کند. هر چند آشیل دونده سریعی است، ولی او هیچ وقت به لاک‌پشت نمی‌رسد، زیرا از زمانی که او به جایی می‌رسد که لاک‌پشت قبلاً آنجا بوده، لاک‌پشت کمی جلوتر رفته. بنابراین او پیش از اینکه لاک‌پشت را پشت سر بگذارد باید بی‌نهایت حرکت را انجام دهد تا به او برسد، که ظاهراً چنین چیزی غیر ممکن است. در دل معماهای زنون سادگی فریبنده‌ای وجود دارند که درک ما از فضا، زمان، حرکت، و علت و معلول را به چالش می‌کشند.

بی‌نهایت در ساده‌ترین، و عادی‌ترین، حوزه‌های ریاضیات خودش را نشان می‌دهد. مثلاً وقتی بچه‌ها با اعداد آشنا می‌شود، قالباً آنها کنجکاوند بدانند بزرگترین عدد چیست، و معمولاً به بزرگترین عددی که نام آن را می‌دانند، مثلاً صد، هزار، یا میلیون، بسنده می‌کنند. ولی خیلی از آنها فوراً به این نتیجه می‌رسند که هیچ عددی نیست که از بقیه بزرگتر باشد، زیرا با اضافه کردن 1 به هر عدد، ما عددی را خواهیم داشت که از عدد قبلی بزرگتر است. یک راه برای گفتن این مسئله این است که بگوییم ”هیچ عدد بزرگتری وجود ندارد“. ارسطو این نوع بی‌نهایت را ’بی‌نهایتِ بالقوه‘ (potential infinity) می‌نامید. توصیف دیگری نیز هست که اندکی مناقشه برانگیز، ولی از نظر ریاضی و فلسفی غنی‌تر است، و آن این است که بگوییم ”تعداد بی‌نهایتی از اعداد صحیح وجود دارند“. ارسطو این نوع بی‌نهایت را ’بی‌نهایتِ واقعی‘ (actual infinity) می‌نامید. امروزه ما واقعیت‌های جهان را از ریاضیات جدا می‌بینیم، ولی ارسطو در زمان خودش آنها را از یکدیگر جدا نمی‌دید، بنابراین کاربرد لغت ’واقعی‘ بی‌مسما است.

بی‌نهایت چیزی است که ما بطور مستقیم با آن روبرو نمی‌شویم، پس چه لزومی دارد درباره آن فکر کنیم؟ دلایل بسیاری برای این وجود دارند. حتی در ریاضیات ابتدایی هم وقتی می‌خواهیم کسری مثل  را بصورت یک عدد اعشاری نشان دهیم، در آنجا نیز با جنبه‌هایی از بی‌نهایت روبرو می‌شویم. برای نمایش دقیق چنین کسرهایی، اعداد اعشاری باید بطور دایم ’تکرار‘ شوند، بعبارتی، دسته‌ای از ارقام تا ابد تکرار می‌شوند. بصورت کلی‌تر، به‌نظر می‌رسد ذهن ما به این ایده نیاز دارد که برخی چیزها ’ تا ابد ادامه دارند‘، چه در فضا و چه در زمان، در آینده یا در گذشته. شاید بی‌نهایت یک پیش‌فرض ذهنی باشد، یعنی یک تاثیر جنبیِ عادی از ذهن ما که همیشه در جستجوی الگوهای مختلف است. سیر تکاملی ما بگونه‌ای بوده که متوجه وجود الگوها در جهان خارج باشیم، چه این الگوها واقعی باشند و چه خیالی. الگوها ارزش ماندگاری دارند. شاید ساده‌ترین الگو این باشد که چیزی تا ابد ادامه داشته باشد، بدون اینکه تغییری در آن حاصل شود، و این همان بی‌نهایت است.

در نتیجه، ما خوشحالیم که می‌توانیم زمان را به صورت چیزی توصیف کنیم که همیشه وجود داشته، و بنابراین منشایی ندارد. گرچه بر اساس آخرین فرضیه‌های کیهان‌شناسیِ نوین، نظریه‌هایی نیز مطرح هستند که می‌گوید زمان آغازی دارد. آن چیزی که باعث می‌شود ما نسبت به فرضیه آغاز زمان اعتراض کنیم این سئوال است که ” اگر زمان آغازی دارد، قبل از آن چه چیزی بود؟“. البته در طرح چنین پرسشی ما این را نادیده می‌گیریم که اگر زمان آغازی داشته باشد، ’قبل از آن‘ دیگر معنی ندارد. ما ترجیح می‌دهیم فضا را بصورت چیزِ بی‌نهایتی درنظر بگیریم، چیزی که جهان در آن بدون محدودیت گسترش یافته، زیرا اگر اینطور نباشد، باید برای فضا مرزی وجود داشته باشد، و بار دیگر ما مجبوریم بپرسیم ’خارج از این حد و مرز چه چیزی وجود دارد؟‘ اینجا نیز ما سئوال اشتباهی را مطرح می‌کنیم. اگر جهان در جایی پایان می‌گیرد، در فرای آن پایان، حتی فضای خالی نیز وجود ندارد. از سوی دیگر، جهان می‌تواند متناهی ولی بدون حد و مرز باشد.

بی‌نهایت در مفهوم زمانی آن، که جاودانگی نام دارد، خصوصاً نقش مهمی را در افکار مذهبی ایفا می‌کند. بی‌نهایت موضوعی متعارف در فلسفه است. این نه فقط موجب شیفتگی هنرمندان بوده، بلکه دانشمندان را نیز تحت تاثیر قرار داده. شما می‌توانید هر گونه ویژگی را به بی‌نهایت نسبت دهید، و هیچ کس هم نمی‌تواند ثابت کند که اشتباه می‌کنید، مگر اینکه در استدلال شما اشتباهی باشد. قطعاً بی‌نهایت مفهوم دلربایی است، موضوعی است پر از نکات ظریف، دام‌های منطقی، معماها، و تناقضات (پارادوکس‌ها).

یکی از بزرگترین تناقض‌هایی که در بی‌نهایت وجود دارد این است که معلوم شده بسیار مفید است. حسابان (calculus)، که بر اساس مفهوم بی‌نهایت بنا شده، انسان را به کره ماه برد، و این توانایی را به او داد که هر روزه میلیون‌ها نفر در سراسر جهان بتوانند پرواز کنند. ریاضیدانان به این نتیجه رسیده‌اند که حتی در حوزه‌هایی مثل ترکیبات (combinatorics)، که در آن ما مجموعه‌های متناهی از اشیاء را می‌شماریم، کنارگذاشتن بی‌نهایت بسیار دشوار است. غالباً الگوها در این اعداد می‌تواند بصورت یک شیء منفردِ نامتناهی، که تابع مولد نام دارد، خلاصه شود و سپس از این تابع مولد می‌توان برای کسب اطلاعات مفید درباره چیزهای کاملاً متناهی استفاده کرد.

ریاضیدانان حتی برای نشان دادن بی‌نهایت علامت مخصوصی را دارند که بشکل ∞ است. از اواخر قرن نوزدهم به بعد، برای انواع مختلفِ بی‌نهایت علامت‌های جدیدی ابداع شده، چیزهایی مثل ₀א یا ω، که ما آنها را در فصل 7 توضیح می‌دهیم. شاید مهمترین سهمی که ریاضیات در فهم ما از بی‌نهایت داشته این حقیقت است که لغت ’بی‌نهایت‘ می‌تواند تفسیرهای بسیار مختلفی داشته باشد. این تفاسیر را می‌توان بدقت تعریف کرد، و از روی این تعاریف می‌توان شباهت‌ها و تفاوت‌های آنها را بصورت منطقی استنتاج کرد.

دیدگاه‌های فلسفی نیز هستند که می‌گوید ریاضیات باید تمام ارجاعاتی که به بی‌نهایت می‌شود را ممنوع کند. ولی تقریباً همه ریاضیدانانی که در سراسر جهان در این حوزه کار می‌کنند نه فقط بی‌نهایت را سودمند می‌دانند، بلکه آن را گریزناپذیر می‌دانند. سئوالات مسحور کننده‌ای نیز درباره بی‌نهایت فیزیکی وجود دارد. مثلاً: آیا جهان متناهی است یا نامتناهی؟ در درون یک سیاه‌چاله چه روی می‌دهد؟ معمولاً وقتی فیزیکدانان با بی‌نهایت روبرو می‌شود، آنها این را نشانه‌ای از دور شدن نظریه خودشان از واقعیت می‌دانند، ولی بسیاری از آنها نیز هستند که ایده یک جهان نامتناهی را دوست دارند. من در فصل 6 روانشناسی که در پشت این تناقضات وجود دارد را بررسی خواهم کرد.

بی‌نهایت مانند یک شمشیر دولبه است. اگر با احتیاط کافی بکار گرفته شود، ابزارهای مهمی مثل حسابان را در اختیار شما قرار می‌دهد، که بیشتر علومِ نوین بر پایه آن قرار دارند. بسیاری از شگفت‌انگیزترین تکنولوژی‌های امروز با استفاده از یکی از جنبه‌های بی‌نهایت اختراع شده‌اند، حتی تکنولوژی کامپیوترهای دیجیتال امروزی، که براساس اعداد دودوییِ متناهی کار می‌کنند، بر اساس علومی مثل شیمی، و فیزیک کوانتوم ساخته شده‌اند، که اساساً همگی آنها از ریاضیاتِ بی‌نهایت استفاده می‌کنند.

با وجود این دست‌آوردها، اگر در روش بکارگیری بی‌نهایت تغییرات کوچکی داده شود، همه اینها می‌تواند به یک سری مهملات بدل شود، و چیزی که باید به آن توجه شود این است که همیشه آسان نیست تا میان چیزهایی که معقولند و آنهایی که نامعقولند خط مشخصی رسم کرد. همه اینها باعث می‌شود بی‌نهایت به یکی از فریبنده‌ترین مفاهیمی بدل شود که تاکنون اختراع شده، البته به شرطی که ’اختراع‘ واژه مناسبی باشد.

رئوس مطالب کتاب

در یک کتاب مقدماتی می‌توان برخی سئوال و جواب‌های اساسی را مطرح کرد، ولی این تنها می‌تواند به موضوعات ژرفتری منجر شود که در پس آنها قرار دارد. در اینجا هدف اصلی من این است که شما درباره این موضوعات فکر کنید، و شما را از اختلاف نظرهای ظریفی آگاه کنم که میان فیلسوفان، خداشناسان، و ریاضیدانان درباره بی‌نهایت وجود دارد. دیدگاه من بر ریاضیاتِ محضِ نوین تکیه دارد، که بر روی موضوعات منطقی تمرکز می‌کنند. غالباً در فیزیک و ریاضیاتِ کاربردی استفاده صوری کمتری از نامتناهی می‌شود، و من فقط موضوعات مربوط به آنها را بطور سطحی مرور می‌کنم.

برای اینکه خودمان را گرم کنیم، ما در فصل اول کارمان را با نُه مثال از موضوعاتی شروع می‌کنیم که به بی‌نهایت مربوط هستند. این موضوعات عبارتند از: معماها، پارادوکس‌ها، و اثبات‌ها. من هر یک از اینها را بطور خلاصه توضیح خواهیم داد، و به این تحلیل می‌پردازیم که آیا روش‌ها یا جواب‌های بکارگرفته شده از نظر منطقی قابل قبول هستند یا نه. برخی از اینها به توضیحات مفصلتری نیاز دارند، و ما بعداً در طول کتاب به آنها بازخواهیم گشت.

در فصل دوم به برخی از سوء برداشتهای رایج که درباره بی‌نهایت وجود دارند اشاره می‌کنیم، و نشان می‌دهیم که چگونه در حساب مقدماتی به طور عادی سر و کله بی‌نهایت ظاهر می‌شود. هدف این است که نشان داده شود چطور بی‌نهایت بطور عمیقی در خیلی از چیزها، حتی در حوزه‌های اصلی ریاضیات نفوذ کرده، و خیلی از سوء برداشتهایی که فکر می‌کنیم آنها را می‌فهمیم نیز روشن شوند.

در فصل 3 ما بر روی موضوعات تاریخی مربوط به بی‌نهایت، از جمله معما‌های مشهور زنون، تمرکز می‌کنیم که عمدتاً به فلسفه و دین مربوط‌ هستند. بی‌نهایت ’یک چیز‘ نیست، بلکه یک مفهوم است، مفهومی که با کارکردِ پیش‌فرضِ ذهن انسان رابطه دارد. به‌نظر می‌رسد معماهای زنون درباره واقعیت فیزیکی باشند، ولی آنها عمدتاً به چگونگی تصور ما از فضا، زمان، و حرکت اشاره دارند. در اینجا ارسطو سهمی مهم (ولی منسوخی) را دارد و آن تمایز میان بی‌نهایتِ واقعی و بی‌نهایتِ بالقوه است. خداشناسان، از اوریجن (Origen) گرفته تا اکویانس (Aquinas)، به بحث ارسطو دامن زده‌اند، و فیلسوفانی مانند امانوئل کانت (Immanuel Kant) این چالش را ادامه دادند. ولی علی‌رغم مقاومت‌های صورت گرفته از سوی فیلسوفانی که مایل بودند به عقاید سنتی خودشان درباره بی‌نهایت وفادار بمانند، این ریاضیدانان بودند که در این راه پیشرفتهای بنیادی حاصل کردند.

در فصل چهارم ما نقطه مقابل بی‌نهایتِ بزرگ، یعنی بی‌نهایتِ کوچک، یا اینفینی‌تِسیمال‌ (infinitesimal)، را بررسی می‌کنیم. اینفینی‌تسیمال‌ها کمیت‌های هستند که بجای اینکه بی‌نهایت بزرگ باشند، بی‌نهایت کوچکند. از لحاظ تاریخی، چنین کمیتهایی پایه و اساس حسابان، یعنی مفیدترین شاخه ریاضیات هستند که تاکنون اختراع شده. ولی آنها همچنین موجب آشفتگی‌های زیادی نیز بوده‌اند، و باعث بوجود آمدن دعواهایی شدند که حل آنها دو قرن طول کشید. نهایتاً این مسئله با استفاده از نسخه‌ای از ’بی‌نهایتِ بالقوه ارسطو‘ (یعنی بی‌نهایتِ کوچکِ بالقوه) حل شد.

در چندجا من عمداً بی‌نهایت را یک مفهوم نامیده‌ام. بهتر است بگویم بی‌نهایت یک ابر-مفهوم است (meta-concept)؛ یا بعبارتی، بی‌نهایت آمیخته‌ای از ایده‌های کم و بیش مرتبط است، که تحت یک نام ظاهر می‌شوند. بیشترین چیزی که موجب تفریح ریاضیدانان و فیلسوفان می‌شود این است که سعی کنند معانی مختلفِ بی‌نهایت را از هم تفکیک کنند و ببینند کدامیک از آنها معقول هستند، و دلیل آن چیست. یک مثال روشن از اینمورد را در فصل 5 خواهید دید و در آنجا به قلمرو کاملاً متفاوتی از بی‌نهایت، یعنی هندسه تصویری (projective geometry)، می‌پردازیم. اقلیدس بر روی یکی از اصولِ موضوعه خودش، که می‌گوید دو خط موازی هیچ وقت همدیگر را قطع نمی‌کنند، خیلی تاکید داشت. ولی نقاشان ایتالیایی دوره رنسانس با تحلیل ژرفانمایی یا پرسپکتیو (perspective)، به نوعی از هندسه دست یافتند که در آن قطع شدن خطوط موازی معقول به‌نظر می‌رسید (البته در بی‌نهایت). اگر شما تابحال در یک ایستگاه قطار ایستاده باشید، با نگاه به خطوط راه‌آهن می‌بینید که آنها چگونه در دور دست به هم می‌پیوندند، و اینجاست که می‌توانید بی‌نهایتِ هندسی را بصورت اجمالی درک کنید.

ما از ریاضیات به دنیای واقعی خواهیم رفت، و در فصل 6 به سئوالاتی نظیر اینکه ’آیا فضا بی‌نهایت است؟‘ می‌پردازیم. در بسیاری از حوزه‌های فیزیک، ظهور یک کمیت بی‌نهایت، که اغلب تکینگی (singularity) نامیده می‌شود، نشانه دور شدن آن نظریه از واقعیت است. برای نمونه، بر طبق نظریه کلاسیک نور، شدت نوری که در اثر تمرکز پرتوها در یک عدسی پدید می‌آید باید بی‌نهایت باشد. حل فیزیکی این مشکل شامل جایگزین کردن پرتوهای نور با امواج نور است. ولی در کیهان‌شناسی، احتمال وجود یک فضای بی‌نهایت خیلی اعتبار دارد.

ما در فصل 7 با بررسی نظریه بسیار مهم کانتور برای شمارش مجموعه‌های بی‌نهایت، و اینکه بی‌نهایت اندازه‌های متفاوتی دارد، دوباره به حوزه بی‌نهایتِ ریاضی بازمی‌گردیم. برای مثال، مجموعه کلیه اعداد صحیح بی‌نهایت است، و مجموعه کلیه اعداد حقیقی (یا اعداد اعشاری) نیز بی‌نهایت است، ولی اساساً این بی‌نهایت‌ها اندازه‌های متفاوتی دارند، و تعداد اعداد حقیقی بسیار بسیار بیشتر از اعداد صحیح است. ’اعدادی‘ که در اینجا مورد بحث هستند، و برای مقایسه بی‌نهایت‌ها از آنها استفاده می‌شود، اعداد اصلي ترامتناهي (Transfinite cardinals) نامیده می‌شوند. برای مقایسه، ما همچنین به روش دیگری اشاره می‌کنیم که برای نسبت دادن یک عدد به یک مجموعه نامتناهی وجود دارد، و اینکار را از طریق مرتب کردن آنها انجام می‌دهیم، که نهایتاً به اعداد ترتیبی ترامتناهي (Transfinite ordinals) می‌انجامد. ما کارمان را با این پرسش خاتمه می‌دهیم که آیا در ریاضیات نوین هنوز هم تمایز دیرینه میان بی‌نهایتِ واقعی و بی‌نهایتِ بالقوه معنی دارد یا نه، و همچنین به بررسی معنی وجودِ ریاضی می‌پردازیم.

 

فصل 1

معماها‌، اثبات‌‌ها، و پارادوکس‌ها

به منظور اینکه به طور فرضی و نَقادانه درباره بی‌نهایت فکر کنیم، در اینجا چند قیاس و سئوال را در نظر می‌گیریم. برخی از اینها جواب درست، و برخی هم جواب اشتباهی را می‌دهند، و برخی هم  واقعاً گیج‌کننده‌ هستند. وقتی به آنها رسیدید، پیش از ادامه مطالعه درباره آنها فکر کنید، و آنها را با هم مقایسه کنید. چرا برخی از آنها معقول به‌نظر می‌رسند ولی برخی نه؟

نُه مورد از جذابیت‌های بی‌نهایت

بزرگترین عدد

بی‌نهایت (∞) بزرگترین عدد است. بنابراین ∞ +1= ∞. اگر از طرفین این معادله ∞ را کم کنیم خواهیم داشت 1=0.

قطر یک مربع

فرض کنید پلکان منظمی را در طول قطر یک مربع واحد رسم کنیم (شکل 1). با یک استدلال ساده ما به این نتیجه می‌رسیم که طول قطر 2 است، زیرا اگر بخشهای عمودی پله را باهم جمع کنیم، حاصل جمع آنها باید 1 شود، و بخشهای افقی نیز همینطور است. اگر تعداد پله‌ها بی‌نهایت شود، و پله‌ها بطور بی‌نهایتی کوچک شوند، این پلکان قطر مربع را تشکیل می‌دهد، و طول این قطر عبارت است حاصل جمع بخش‌های افقی و عمودی، بنابراین طول قطر آن 1+1=2 می‌شود.

شکل 1. شکل‌های سمت چپ و وسط پله‌ها و کوچک شدن هر چه بیشتر آنها را نشان می‌دهد. شکل سمت راست حالتی را نشان می‌دهد که تعداد پله‌ها بی‌نهایت شده.

مساحت یک دایره

دایره یک منحنی‌ است که از تعداد بی‌نهایتی از خطوطِ بی‌نهایت کوتاه تشکیل شده. همانطور که در شکل 2 نشان داده شده، با وصل کردن آنها به مرکز دایره، تعداد بینهایتی مثلث ایجاد می‌شود، که هر یک ارتفاعی برابر با شعاع دایره، یعنی r، دارند و مساحت هر مثلث برابر 1/2rb است، که b طول قاعده مثلث است. بنابراین اگر مجموع مساحت همه این مثلث‌ها را حساب کنیم، مساحت دایره 1/2r برابرِ محیط آن است. محیط دایره 2πr است، بنابراین مساحت آن برابر خواهد بود با 1/2r×2πr=πr².

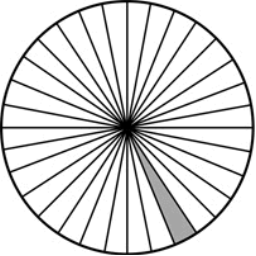
شکل 2. تعداد بی‌نهایتی از مثلث‌ها (که فقط 32 عدد از آنها دراینجا نشان داده شده) و یکی از آنها سایه خورده.

کلید لامپ

در زمان 0، کلید لامپ خاموش است. پس از یک‌دوم ثانیه من آن را روشن می‌کنم. یک چهارم ثانیه بعد آن را خاموش می‌کنم. یک هشتم ثانیه بعد دوباره آن را روشن می‌کنم. یک شانزدهم ثانیه بعد آن را خاموش می‌کنم، و به همین ترتیب. هر یک از بازه‌های زمانی که من کلید را خاموش یا روشن می‌کنم نصف بازه زمانی قبلی است. بعد از سپری شدن یک ثانیه، آیا لامپ روشن است یا خاموش؟

تعداد گوی‌های موجود در کیسه

من یک کیسه خالی و تعداد بی‌نهایتی گوی دارم، که بصورت 1, 2, 3, … شماره گذاری شده‌اند. در زمان 0، من گوی‌های شماره 1 الی 10 را در کیسه می‌گذارم و گوی شماره 1 را درمی‌آورم. ½ ثانیه بعد، من گوی‌های شماره 11 الی 20 را در کیسه می‌گذارم و گوی شماره 2 را از کیسه در می‌آورم.  ¾ثانیه بعد، من گوی‌های شماره 21 الی 30 را در کیسه می‌گذارم و گوی شماره 3 را خارج می‌کنم. در زمان 7/8 ، من گوی‌های شماره 31 الی 40 را در کیسه می‌گذارم و گوی شماره 4 را خارج می‌کنم، و به همین ترتیب. هربار تعداد گوی‌های موجود در کیسه به میزان 9 عدد افزایش می‌یابد. پس از سپری شدن یک ثانیه، چه تعداد گوی در کیسه قرار دارند؟

عدد یک سوم بصورت اعشاری

اگر ما سعی کنیم عدد  1/3را بصورت اعشاری نمایش دهیم، بدلیل اینکه حاصل تقسیم 10 بر 3 برابر 3، و باقیمانده آن 1 است، این عدد هیچگاه پایانی ندارد، و با ادامه تقسیم، ما هربار عدد 3 را حاصل می‌کنیم؛ بعبارتی 0.3333… تا ابد ادامه دارد. اگر ما در مکان مشخصی کارمان را متوقف کنیم، مثلاً در 0.33333، این عدد از 1/3 کوچکتر است، زیرا اگر آن را در 3 ضرب کنیم، حاصل 0.99999 خواهد بود که به میزان 0.000001 از عدد 1 کوچکتر است. پس آیا دنباله بی‌نهایتی از 3ها، که بصورت 0.333…3... نوشته می‌شود، از 1/3 کوچکتر است یا دقیقاً مساوی آن است؟

مربع‌ها و اعداد

ما این مثال را از یکی از کتابهای گالیله بنام  ”بحث‌ها و اثبات‌های ریاضی در رابطه با دو علم جدید[1]“ اقتباس کرده‌ایم. در اینجا گفتگویی میان سه شخص بنام‌های سالویاتی (Salviati) و سیمپلی‌سیو (Simplicio) و ساگرِدو (Sagredo) صورت می‌گیرد:

سالویاتی: ما نمی‌توانیم از کمیات بی‌نهایت به صورتی سخن بگوییم که گویی یکی از آنها کوچکتر یا برابری دیگری است. مثلاً، من فرض را بر این می‌گیرم که شما می‌دانید کدام یک از اعداد مربع هستند و کدامیک نیستند.

سیمپلی‌سیو: من خوب می‌دانم که یک عدد مربع عددی است که از ضرب یک عدد دیگر در خودش حاصل می‌شود؛ بنابراین اعداد 4، 9، و ... اعداد مربعی هستند که از ضرب اعداد 2،  3و غیره در خودشان حاصل شده‌اند.

سالویاتی: بسیار خوب؛ پس شما همچنین می‌دانید همانطور که مربع‌ها حاصل ضرب اعداد در خودشان هستند، آن اعداد نیز ریشه این مربع‌ها نامیده می‌شوند. بنابراین اگر من ادعا کنم که تعداد همه اعداد، چه مربع باشند و چه غیر-مربع، بیشتر از تعداد اعداد مربع به تنهایی است، آیا درست گفته‌ام یا نه؟

سیمپلی‌سیو: مطمئناً اینطور است.

سالویاتی: اگر من سئوال کنم چه تعداد عدد مربع وجود دارد، ممکن است کسی پاسخ دهد به هر تعدای که ریشه وجود دارد به همان اندازه هم مربع وجود دارد، زیرا هر مربع ریشه خودش را دارد و هر ریشه مربع خودش را، هیچ مربعی هم بیش از یک ریشه ندارد، و یک ریشه هم بیش از یک مربع ندارد ... و این معلوم است، ما باید بگوییم به تعدادی که عدد وجود دارد مربع نیز وجود دارد، زیرا آنها به همان تعدادی هستند که ریشه‌های آنها، و همه اعداد ریشه یک عددی هستند.

ساگرِدو: پس تحت این شرایط چه نتیجه‌ای باید گرفت؟

سالویاتی: آنچه من تا اینجا می‌بینم تنها این است که تعداد کل اعداد بی‌نهایت است، و نسبت دادن ’برابر‘، ’بزرگتر‘، و ’کوچکتر‘ در مورد کمّیّت‌های نامتناهی قابل استفاده نیست، بلکه فقط درمورد کمّیّت‌های متناهی کاربرد دارد.

هتل هیلبرت

در یکی از درس‌هایی که داوید هیلبرت (David Hilbert) در سال 1924 ارائه داد، او با کمک گرفتن از یک هتل فرضی، نظریه اعداد نامتناهی کانتور (اعداد اصلی ترامتناهی) را توضیح داد. این هتل تعداد بی‌نهایتی اطاق دارد که بصورت 1, 2, 3, … شماره‌گذاری شده‌اند. فرض کنید درحالی که همه اطاق‌های این هتل از قبل پر شده مهمان جدیدی از سر می‌رسد. در نگاه اول اینطور به‌نظر می‌رسد که این مهمان جدید باید به هتل دیگری برود، ولی ناگهان فکری به ذهن مدیر هتل می‌رسد. او از تمام مهمانان هتل می‌خواهد که اطاق‌های خود را ترک کنند و به اطاقی بروند که شماره آن یکی بیشتر از شماره اطاق آنها است. این یعنی، مهمان اطاق 1 به اطاق 2، مهمان اطاق 2 به اطاق 3، مهمان اطاق 3 به اطاق 4، و ...، بروند. همه آنها هم‌زمان حرکت می‌کنند. در اینصورت، هنوز هم کلیه مهمانان یک اطاق دارند، و بطور معجزه‌آسایی اطاق شماره 1 نیز خالی شده، و مهمان تازه وارد می‌تواند به آن اطاق برود.

در یک هتلِ متناهی که تعداد معینی اطاق دارد چنین چیزی امکان ندارد: زیرا آن مهمانی که در اطاقی با بزرگترین عدد ساکن است جایی برای رفتن ندارد. ولی در هتل هیلبرت هیچ اطاقی وجود ندارد که شماره آن بزرگترین عدد باشد.

در اینجا ممکن است دو سئوال دیگر مطرح شود:

·      فرض کنید کاروانی از سر می‌رسد که شامل تعداد بی‌نهایتی از مهمانان جدید است، که آنها نیز مهمان شماره 1، مهمان شماره 2، مهمان شماره 3 و ... نامگذاری شده‌اند. آیا هنوز هم هتل هیلبرت می‌تواند با جابجا کردن مهمانان قبلی همه مهمانان جدید را اسکان دهد؟

·      اگر تعداد بی‌نهایتی کاروان، که هر یک از آنها 1, 2, 3, … نامگذاری شده‌اند، و هر یک تعداد بی‌نهایتی مهمان جدید را در خودشان دارند یکباره از راه برسند، آیا باز هم هتل هیلبرت می‌تواند آنها را اسکان دهد؟

استدلال گراندی درمورد آفرینش

در سال 1703 گوئیدو گراندی (Guido Grandi) کتابی بنام ” تربیع دایره و هذلولی توسط تعداد بی‌نهایتی از منحنی‌های هندسی“ را منتشر کرد. در آنجا او سری نامتناهی زیر را در نظر گرفت:

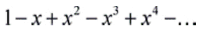
بر طبق قضیه دوجمله‌ای (binomial theorem)، این سری برابر است با 1/(1+x). اگر x را برابر 1 بگیریم، نتیجه می‌گیریم که

از سوی دیگر ما می‌توانیم آنها را بصورت زیر هم گروه‌بندی کنیم و نتیجه گیری کنیم که

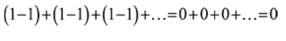
بنابراین ½=0، که گراندی آن را بعنوان استدلالی برای خلق جهان از هیچ توسط خدا عنوان می‌کرد. گروه‌بندی دیگری که برای این سری می‌توان در نظر گرفت بصورت زیر است:

بنابراین 0=1، که به همان اندازه گیج‌کننده است.

حل معماهای ذکرشده و تشریح آنها

از دیدگاه ریاضیاتِ امروزی، بیشتر مثالهای ذکر شده را می‌توان بدون متوسل شدن به ایده‌های جدید حل کرد. بعضی از آنها نیز هستند که به بررسی‌های بیشتری نیاز دارند، که در فصل‌های بعدی به آنها می‌پردازیم.

توضیح در مورد بزرگترین عدد

استدلالی که اینجا ذکر شده بطور آشکار غلط است، ولی چرا؟ یک مشکل می‌تواند این باشد که ما بی‌نهایت را بعنوان یک عدد در نظر گرفته‌ایم، و در این‌صورت این سئوال بوجود می‌آید که ”اصلاً عدد چیست؟“ استنتاج‌های ذکر شده فقط برای اعداد عادی معتبر هستند، که در هر حال ∞ نمی‌تواند یک عدد عادی باشد. ولی ریاضیدانان یک سری معانی را برای ∞  تعریف کرده‌اند که کمتر مناقشه‌ برانگیزند، و براساس آنها، بی‌نهایت (نوع جدیدی) عدد است. در آنجا عباراتی مثل ’ ∞ +1=∞‘ از لحاظ ریاضی قابل قبول است، هر چند برای روشنتر شدن زمینه، از علامت متفاوتی استفاده می‌شود. چیزی که در اینجا غیرقابل قبول است کم کردن ∞ از طرفین معادله است، زیرا اگر بخواهیم قواعد عادی حساب پابرجا بمانند، نمی‌توان برای کمیتهای نامتناهی تفریق را تعریف کرد.

توضیح در مورد قطر یک مربع

به منظور اینکه این مثال ملموس‌تر شود، ریاضیدانان این استدلال را به صورت دیگری مطرح می‌کنند و تعداد پله‌ها (یعنی n) را متناهی می‌گیرند، ولی فرض می‌کنند n به سمت بی‌نهایت میل می‌کند. این شبیه این است که بگوییم ” n متناهی می‌ماند ولی بصورت نامحدودی بزرگ می‌شود.“ اینجا یک منحنی حدی وجود دارد که بخوبی تعریف شده، و آن قطر مربع است. ولی بر طبق قضیه فیثاغورث، طول قطر این مربع 2 نیست، بلکه  است.  برخی اوقات ادعا می‌شود که منحنی حدی قطر مربع نیست، بلکه یک خط بی‌نهایت پرپیچ و خم است که مرتب درحال گذر از آن است. ولی اینطور نیست. طول منحنی حدی با حدِ طول پله‌ها یکی نیست، فقط همین.

توضیح در مورد مساحت یک دایره

در اینجا استدلالِ ذکر شده جواب درستی را می‌دهد، و می‌توان آن را توجیه کرد. ارشمیدس نیز از یک روش یونانی استفاده کرد که تهی‌سازی (exhaustion) نام داشت، ولی همانطور که در فصل 4 توضیح خواهیم داد، او بدون اینکه اثباتی داشته باشد، فرض می‌کرد که دایره مساحت کاملاً تعریف ‌شده‌ای ندارد. امروزه ما معمولاً بجای آن به حسابان متوسل می‌شویم. ایده این است که از تعداد n برش متناهی بسیار نازک استفاده شود، که همه آنها یک شکل و یک اندازه هستند و قسمت بیرونی آنها بصورت خط راست درآمده تا مثلث‌هایی را تشکیل دهند. آنها دقیقاً دایره اصلی را نمی‌پوشانند، ولی اگر مساحت‌های آنها را باهم جمع کنیم، بطور خیلی نزدیکی مساحت دایره را تقریب می‌زنند.

مساحت یک مثلث برابر است با نصف قاعده ضرب در ارتفاع آن، بنابراین کل مساحت عبارت است از نصف محیط ضرب در ارتفاع. محیط یک دایره برابر 2πr است. ارتفاع هر مثلث نیز به شعاع دایره، یعنی r، بسیار نزدیک است. بنابراین مساحت کلی خیلی به ½.2 πr.r= πr²  نزدیک می‌شود. همانطور که در فصل 4 توضیح داده خواهد شد، با بکارگیری اصول منطقی حسابان، می‌توان اثبات کرد که همانطور که n به سمت بی‌نهایت میل می‌کند، حد مساحت کلیه مثلث‌ها دقیقاً برابر πr² است. تعریف مساحت یک دایره در حسابان همین حد است، و از فرض اینکه مساحت وجود دارد یا نه اجتناب می‌کند. در عوض ما باید اثبات کنیم که مساحتی که به این صورت تعریف می‌شود کلیه خواص مورد نظر را دارد.

توضیح در مورد مسئله کلید لامپ

از لحاظ ریاضی، رویه‌ای که در اینجا تعریف شده وضعیت کلید را برای کلیه زمان‌های کمتر‌ از یک ثانیه تعریف می‌کند. این در مورد وضعیت کلید در زمانی که دقیقاً یک ثانیه سپری شده چیزی به ما نمی‌گوید. همه روندهای نامتناهی دارای معنی معقولی نیستند، و این یکی از آنها است.

از نظر فیزیکی، ما سریعاً به حالتی می‌رسیم که سرعت جابجایی کلید به حالتی سریعتر از سرعت نور می‌رسد، که بر طبق نظریه نسبیت غیر ممکن است. پیش از آنکه چنین شود، اصطکاک باعث ذوب شدن کلید می‌شود، پیش از آن هم، به احتمال زیاد لامپ ما خواهد سوخت!

توضیح در مورد تعداد گوی‌های موجود در کیسه

احتمالاً فکر می‌کنید که جواب آن بی‌نهایت باشد، ولی زیاد تند نروید!

لطفاً موضوعات عَمَلی را نادیده بگیرید. این یک مثال فرضی در دنیای غیر-واقعی است. می‌توان آن را طوری فرمول‌بندی کرد که از لحاظ ریاضی معقول به‌نظر برسد.

در مرحله‌ n، کیسه حاوی 9n گوی است، ولی ما نمی‌توانیم فقط اجازه دهیم که n به سمت بی‌نهایت میل کند تا به این نتیجه برسیم که تعداد ’نهایی‘ گوی‌های موجود در کیسه بی‌نهایت است. حدِ تعداد گوی‌ها در کیسه با تعداد گوی‌‌های کیسه یکی نیست. با توجه به این مورد، این شبیه مثالی است که در مورد قطر پلکانی مربع مطرح شد.

در واقع پس از سپری شدن یک ثانیه هیچ گویی در کیسه نیست. برای اینکه به دلیل آن پی ببرید توجه کنید که گوی n در مرحله nام برداشته می‌شود، و هیچ موقع دوباره در کیسه قرار نمی‌گیرد. کلیه گوی‌هایی که در کیسه قرار داده می‌شوند برای مدتی آنجا هستند و سپس دوباره برداشته می‌شوند. اگر آن را جستجو کنید، کیسه خالی است.

توضیح در مورد عدد یک سوم بصورت اعشاری

می‌توان برای یک عدد اعشاری نامتناهی معنی منطقی محکمی ارائه داد. برای توضیحات بیشتر به فصل 4 رجوع کنید. فعلاً فرض کنید که

S= 0.333333333…

پس

10S= 3.333333333…= 3 + S

بنابراین، 9S=3، پس S = 3/9 = 1/3.

هرچند توقف در هر مرحلهِ خاص عددی را می‌دهد که از 1/3 کمتر است، ولی با اضافه شدن ارقام اعشاری بیشتر این اختلاف بسرعت کاهش می‌یابد. یک دنباله نامتناهی که بطور دلخواهی کوچک می‌شود دارای اختلاف حدی صفر است. تناقضی ظاهری که وجود دارد به این دلیل است که هیچگاه به آن مقدار نمی‌رسد.

توضیح در مورد مربع‌ها و اعداد

این موضوعِ قابل‌توجهی است که خیلی پیش از اینکه کانتور نظریه شمارش مجموعه‌های نامتناهی خودش را توسعه دهد، گالیله حدود 200 سال پیش از آن به همان نتیجه رسیده بود (به فصل 7 رجوع کنید). از نقطه نظر کانتور، بیشتر چیزهایی که سالویاتی در آخر گفتگو می‌گوید صحیح است، به غیر از اینکه می‌توان ’مساوی‘، ’بزرگتر‘، و ’کوچکتر‘ را درمورد کمّیت‌های نامتناهی نیز بکار برد. ولی آنها دقیقاً مانند کمیت‌های متناهی رفتار نمی‌کنند، و شما می‌توانید استدلال کنید که منظور سالویاتی نیز واقعاً همین بوده.

توضیح در مورد هتل هیلبرت

داستان هتل هیلبرت برپایه چهارچوب مجموعه‌های نامتناهی کانتور قرار دارد، یعنی اگر ’تعداد اعضای‘ مجموعه اعدادِ صحیح (که یک عدد اصلي ترامتناهي است) را به ℵ₀ نشان دهیم، آنگاه 1+ℵ₀ = ℵ₀ (علامت ℵ  در زبان عبری ’الف‘ نامیده می‌شود). ایده زیربنایی این است که میان مجموعه N (مجموعه اعداد صحیح) و زیرمجموعه آن M (مجموعه اعداد صحیح بزرگتر از 1) نگاشتی (map) برقرار کنیم. این نگاشت باید یک تناظر یک-به-یک باشد، یعنی هر یک از اعضای متفاوت N باید با اعضای متفاوت M متناظر باشند، و کلیه اعضای M به این طریق از N ناشی می‌شوند. شکل 3 چگونگی انجام اینکار را نشان می‌دهد. خط بالایی 1+ℵ₀ و خط پایینی  ℵ₀را نشان می‌دهند، و پیکان‌ها ثابت می‌کنند که آنها یکی هستند:

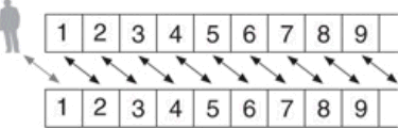
شکل 3. اگر همه اطاق‌ها یک خانه حرکت کنند، اطاق 1 خالی می‌شود.

فرض کنید کاروانی متشکل از تعدادِ بی‌نهایتی مسافر از راه برسند (شکل 4). حالا مدیر هتل هر یک از مهمانان موجود را از اطاق‌های شماره n  به شماره 2n (یعنی اطاق‌های زوج) انتقال می‌دهد. آنگاه هر مسافر کاروان که شماره آن m باشد می‌تواند در اطاقی که شماره آن 2m -1 است (یعنی اطاق‌های فرد) اسکان داده شود. حالا تمام مسافران می‌توانند اسکان داده شوند. در نمادگذاری کانتور این بصورت ℵ₀+ℵ₀ = ℵ₀ نمایش داده می‌شود.

 

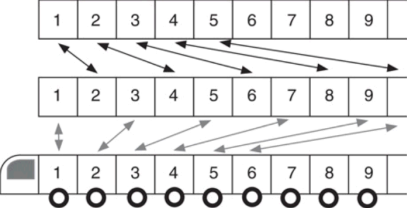
شکل 4. طریقه اسکان دادن یک کاروان که شامل تعداد بی‌نهایتی از مسافران است.

حالا اگر تعداد بی‌نهایتی کاروان از راه برسند که هر یک شامل تعداد بی‌نهایتی مهمان هستند، مدیر هتل مسافران را بصورتی که در شکل 5 نشان داده شده اسکان می‌دهد. به این صورت که جهت پیکان‌های مورب را دنبال می‌کنیم و بعد از رسیدن به انتهای هر پیکان، به اطاق بعدی در ردیف بالایی بازمی‌گردیم. در این حالت نیز کلیه مهمانان می‌توانند اسکان داده شوند، و بر اساس نمادگذاری کانتور، این ثابت می‌کند که  ℵ₀ × ℵ₀ = ℵ₀.

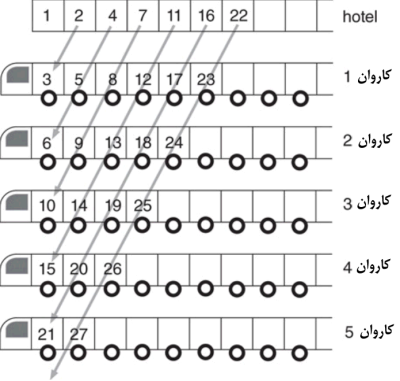
شکل 5. ترتیب ’اوریب‘ مدیر هتل. در اینجا اعداد 2-3، 4-5-6، 7-8-9-10 و غیره به طرف چپ کج شده‌اند.

اگر بخواهیم محاسبات عجیبی را که با ℵ₀  انجام دادیم معقول به‌نظر برسند، باید ℵ₀ را بصورت بی‌نهایت تعبیر کنیم، و اگر شما 1 را به بی‌نهایت اضافه کنید، آن را دو برابر کنید، شما باز هم باید بی‌نهایت را حاصل کنید. کشف خارق‌العاده کانتور این بود که حساب اعداد ترانامتناهی خیلی غنی‌تر از اینها است. ما دلیل این موضوع را در فصل 7 خواهیم دید.

توضیح درمورد استدلال گراندی برای آفرینش

در سال 1730 لئونارد اویلر نیز محاسبه مشابه‌ای را انجام داد و خوشحال بود که ½ را بعنوان مجموع بدست آورده. به منظور اینکه یک دنباله نامتناهی معنی دار باشد، ریاضیدانان به این نتیجه رسیدند که آنها باید همگرا (converge) باشد، به این صورت که اگر شما به تعداد کافی جملات را باهم جمع کنید، این مجموع به اندازه دلخواهی به یک مقدار ثابت نزدیکتر می‌شود (به فصل 4 رجوع کنید). اگر مقدار x بین -1 و 1 باشد (-1< x < 1) این دنباله همگرا است، ولی اگر x=1 باشد اینطور نیست. بنابراین قرار دادن مقدار x=1 مجاز نیست.

گرچه این پایان داستان نیست. اگر بعد از تعداد متناهی از جملات، جمع را متوقف کنیم، مقداری که اویلر بدست آورد، یعنی ½، میانگین دو عدد 0 و 1 است، بنابراین حسی به ما می‌گوید که این مقدار بهتر از هر مقدار دیگری نشان دهنده رفتار کلی این دنباله است. ملاحظاتی از این دست به نظریه ’جمع‌پذیری‘ دنباله‌هایی منجر شد که همگرا نیستند، و اینجا حاصل مجموع ½ است.

 

 

فصل 2

رويارویي با بی‌نهایت

ما در حرفهای روزمره خودمان بطور گاه و بی‌گاه از لغت ’بی‌نهایت‘ استفاده می‌کنیم، بنابراین تا پیش از اینکه به جنبه‌های ظریف‌تر این موضوع بپردازیم، بد نیست به مطالب ابتدایی درباره بی‌نهایت اشاره کنیم. من بر روی دو موضوع تمرکز می‌کنم:

·      بی‌نهایت لغتی نیست که ما فقط برای نامیدن اعداد بسیار بزرگ از آن استفاده کنیم. ما غالباً برای این منظور، یا برای شاعرانه‌تر کردن یا مهیج‌تر کردن جملات خودمان، یا صرفاً از روی ناآگاهی از این لغت استفاده می‌کنیم. ولی روی ‌هم رفته، لغت ’بی‌نهایت‘ در ریاضیات و فلسفه مفهوم متفاوتی دارد، به این معنی که ما آن را یک حد بسیار بزرگ فرض نمی‌کنیم، بلکه آن را بعنوان نبودِ هرگونه حدی در نظر می‌گیریم.

·      بی‌نهایت فقط یک اختراع مبهم و پیچیده در ریاضیات پیشرفته نیست. در ریاضیات دبستانی هم ما خیلی زود با آن روبرو می‌شویم. اولین نِمود آن این است که ’هیچ عدد صحیحی وجود ندارد که بزرگتر از بقیه باشد‘. هنگامی که ما اعداد اعشاری را یاد می‌گیریم، و آنها را با مفهوم کسر، که زودتر یادگرفته‌ایم مقایسه می‌کنیم، بی‌نهایت بصورت‌ معنی‌دارتری خودش را نشان می‌دهد.

متناهی و نامتناهی

من قصد ندارم بی‌نهایت را تعریف کنم، زیرا این لغت معانی زیادی دارد، معانی که به تدریج به آنها اشاره خواهم کرد. بعنوان یک قاعده کلی، یک عدد (چه صحیح، چه کسر، چه اعشاری، و چه هر عدد دیگری) تنها وقتی متناهی است که کوچکتر از عدد دیگری در دنباله (1, 2, 3, …) باشد، و اگر اینطور نباشد آن عدد نامتناهی است (برای اعداد منفی، ابتدا باید آنها را مثبت فرض کنید). یک شیء فقط وقتی متناهی است که اندازه آن متناهی باشد، و در غیراینصورت نامتناهی است. یک دایره متناهی است، ولی خطی که تا ابد ادامه دارد اینطور نیست.

برای اندازه‌گیری مقیاس‌های زیادی وجود دارد، و یک شیء با یک مقیاس می‌تواند متناهی باشد، ولی همان شیء در مقیاس دیگری می‌تواند نامتناهی باشد. مثلاً محیط و مساحت یک دایره متناهی است، ولی از تعداد نامتناهی نقطه تشکیل شده. منحنی برف‌دانه (یک فراکتال fractal)، از یک مثلث متساوي‌الاضلاع حاصل می‌شود که از اضافه کردن مثلث‌های متساوي الاضلاع کوچکتری به اندازه یک سوم طول ضلع در میان طول هر یک از اضلاع ساخته می‌شود (شکل 6 بالا). طول این منحنی نامتناهی است ولی در یک مساحت متناهی محصور شده‌اند. طول کمان یک هذلولی که با معادله y=1/x نشان داده می‌شود، و از x=1 تا بی‌نهایت ادامه دارد (شکل 6 وسط) بی‌نهایت است، ولی مساحت ناحیه‌ای که میان این منحنی و محور xها قرار دارد (و بصورت خاکستری نشان داده شده) متناهی است. در سال 1644 ریاضیدان و فیزیکدان ایتالیایی اوانجلیستا توریچلی (Evangelista Torricelli) ثابت کرد که هنگامی که این منحنی حول محور xها دوران کند، دارای سطحی بی‌نهایت خواهد بود که دارای حجمی متناهی است (شکل 6 پایین). در واقع حجم آن دقیقاً برابر π است. این سطح به شیپور جبرئیل یا شیپور تویچلی معروف است، و در آن زمان برای ریاضیدانان به یک چالش جدی در رابطه با مفهوم نامتناهی بودن تبدیل شده بود.

شکل 6: شکل بالا، مراحل مختلف ساخت یک منحنی برف‌دانه. شکل وسط، مساحت زیر یک هذلولی. شکل پایینی، شیپور جبرئیل دارای یک مساحت نامتناهی ولی حجمی متناهی است.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

 

فصل 3

دیدگاه‌های تاریخی درباره بی‌نهایت

تاریخ مباحث مربوط به بی‌نهایت و کاربردهای آن به 2500 سال قبل، یعنی در زمانی که آناگزامایاندر (Anaximander) فرضیه اَپریون (apeiron) خود را مطرح کرد باز‌می‌گردد. در آن زمان سه حوزه علمی مطرح بود: الهیات، فلسفه، و ریاضیات (البته اخیراً کشفیاتی هم در زمینه فیزیک صورت گرفته بود، ولی من آنها را تحت حوزه ریاضیات طبقه کرده‌ام). شرح جامع همه این موارد تلاش عمده‌ای را طلب می‌کند، بنابراین من خلاصه ایده‌ها و اشخاصی را شرح خواهم داد که در این دوره مطرح بوده‌اند. از نظر الهیاتی، تمرکز من بر روی الهیات مسیحی خواهد بود، و صرفاً تلاش می‌کنم برخی از موضوعات الهیاتی را مطرح کنم که بر سر آنها تضاد و مشاجره وجود داشته.

از زمان آناگزامایاندر به بعد، توسعه ریاضیات را می‌توان به چهار دوره و مکانِ عمده تقسیم بندی کرد. در آغاز، فعالیت‌های اصلی در یونان صورت می‌گرفت، که نمونه‌های بارز آن کتاب اصولِ اقلیدس (Elements) و آثار فلسفی ارسطو (Aristotle) هستند. در هزاره بعدی، این فعالیت‌ها به چین، هند، و خاورمیانه انتقال یافت. بدنبال رُنسانس، یعنی از سال 1400 میلادی به بعد، بیشتر اکتشافات ریاضی در اروپا صورت گرفتند. جامعه ریاضی در قرن بیستم به یک جامعه جهانی تبدیل شد. ولی این فقط یک شرح کلی برای زنجیره‌ای از وقایع پیچیده است که فرهنگ‌های مختلفی در آن سهیم بوده‌اند و در نواحی گوناگونی اتفاق افتاده.

تا پیش از قرن بیستم، مذهب و فلسفه تاثیر عمده‌ای بر روی تفکر اصلی ریاضی داشتند. این سه حوزه بطور نزدیکی درهم تنیده بودند، آنقدر نزدیک که امروزه برای ما تعجب‌آور است. الهیات مسیحی تفکر ارسطو را احیا کرد و درک او از بی‌نهایت را به عنوان یکی از ارکان اصلی تفکر خودش درباره طبیعت، و وجود خدا، قرار داد. بی‌کران بودن اعداد طبیعی پایه اصلی استدلالات دینی قرار گرفت. فیلسوفان شروع به بحث در مورد موضوعات مربوط به اصول منطق و ریاضیات کردند. در این میان، ریاضیدانان تلاش می‌کردند تا اکتشافات ریاضی خودشان را با عقاید شخصی‌ و فلسفی خود وفق دهد، و چیزی که موجب الهام‌شان بود استنتاجات آنها بود.

در آغاز قرن بیستم، و با توسعه پایه‌های ریاضیات که بر اصول موضوعه تکیه داشتند، این پیوندها شروع به از هم گسیختن کردند. اصول موضوعهِ نظریه مجموعه‌ها آنقدر فنی شد که برای فیلسوفانی که تقریباً فلسفه ریاضی را رها کرده بودند، جذابیتش را از دست داد. البته استثناهایی نیز وجود داشت، که از مهمترین آنها می‌توان به فیلسوفانی نظیر برتراند راسل (Bertrand Russell) و لودویگ ویتگن‌اشتاین (Ludwig Wittgenstein) اشاره کرد که با هم مخالف بودند. طعنه‌آمیز است که راسل یکی از مهم‌ترین کسانی بود که مسئول بنا کردن اصول ریاضیات بر اساس نظریه بسیار فنی مجموعه‌ها بود (که اینکار را با همکاری فیلسوف دیگری بنام آلفرد نورث وایت‌هد انجام داد). حالا دیگر اکثرِ ریاضیدان‌ها به آنچه فلاسفه می‌گفتند توجه نمی‌کردند، مخصوصاً به کسانی مانند ویتگن‌اشتاین  که می‌گفتند هر کاری که ریاضیدانان انجام می‌دهند اشتباه است. مذهب نفوذ سیاسی خودش را از دست داده بود؛ در سراسرِ جهانِ توسعه یافته، عقاید مذهبی انکار می‌شدند، هرچند شدت آن در کشورهای مختلف باهم فرق داشت. به ویژه، ریاضیدانان هیچ قید و بندی را از طرف آموزه‌های کلیسا بر خودشان حس نمی‌کردند.

اتخاذ بنیان‌های دقیق برای ریاضیات، که بر اصول موضوعه تکیه داشتند، الزاماً موجب حل مسائل منطقی نشد، ولی بطور قابل ملاحظه‌ای آنها را روشن ساخت. بی‌نهایت هنوز هم یک معما بود، ولی حداقل ما می‌دانستیم که درباره چه صحبت می‌کنیم و چرا این موضوع یک معما است. همراه با این پیشرفت‌ها، دیدگاه جدیدی نیز در وجود ریاضی پدید آمد، و آن این بود که حالا دیگر نیازی نبود که مفاهیم ریاضی الزاماً مدل مستقیمی برای واقعیت‌های بیرونی باشند، یا اصلاً ارتباطی با واقعیت داشته باشند. به شرطی که در کار ریاضیدانان تناقضات منطقی وجود نداشته نباشد و با مفاهیم موجود رابطه داشته باشد، آنها برای خلق مفاهیم جدید ریاضی آزاد هستند. همانطور که کانتور گفته بود ”جوهر ریاضیات در رهایی آن است“.

هشدار: مطالب زیر ممکن است حاوی بی‌نهایت باشند!

مثال‌هایی که در فصل 1 مطرح شدند نشان‌دهنده خطرات و قدرت بی‌نهایت بعنوان چهارچوبی برای پیشرفت ریاضیات هستند. بحث‌هایی که تقریباً یکسان بنظر می‌رسند می‌توانند در یک زمینه معتبر و در زمینه دیگری مغالطه آميز باشند. از لحاظ تاریخی، تمایزهای ظریفی از این نوع اغلب از جدال‌های ریاضی و فلسفی پدیدار می‌شوند. در ریاضیات مفهوم ’بی‌نهایت‘ نه از پیش‌معلوم، و نه منحصر بفرد است، در عوض به زمینه‌ موضوع بستگی دارد و بر اساس نیازهای منطقی موضوع تعریف می‌شود. فلاسفه نیز برای بی‌نهایت تفسیرهای مختلفی قایل هستند.

موضوع اصلی مطرح در ریاضیات این است که آیا خواصِ آشنای روندها و اشیاء متناهی برای روندها و اشیاء بی‌نهایت نیز معتبر می‌ماند یا نه. بی‌نهایت تنها موضوعی نیست که در این باره مطرح است، اعداد منفی نیز در چنین وضعیتی قرار داشتند. اولین سابقه‌ای که درباره اعداد منفی وجود دارد در یک کتاب چینی بنام  ’ نه فصل درباره هنر ریاضی‘ دیده می‌شود که تاریخ آن به سلسله هان (Han)، یعنی از سال 202 قبل از میلاد تا 220 بعد از میداد برمی‌گردد. ریاضیدانان چینی و هندی آزادانه از اعداد منفی استفاده می‌کردند، ولی بطور ضمنی فرض می‌کردند که آنها از همان قواعد حساب پیروی می‌کنند که اعداد مثبت از آنها پیروی می‌کند. هنگامی که سر و کله اعداد مختلط (complex numbers) پیدا شد، یعنی دستگاه‌ اعدادی که در آن -1 داری ریشه دوم است، همین مفروضات بطور ضمنی پذیرفته شدند. ولی اینها بسیار اسرار آمیز بودند. سرانجام ریاضیدانان یادگرفتند چگونه توسعه‌های مربوط به سیستم اعداد را بطور انتزاعی تعریف کنند، قواعد اصلی که برای کار با آنها لازم است را فهرست کنند، و اثبات کنند که آیا این سیستم‌های توسعه‌یافته می‌توانند در مورد هر یک از این قواعد صدق کنند یا نه. استفادهِ ددکیند از بخش‌های اعداد گویا برای تعریف اعداد حقیقی نمونه‌ای از اینها است.

برخورد منطقی با بی‌نهایت نیز از همین الگو پیروی می‌کرد. در آغاز یک فرض ساده مطرح بود که خصوصیات اصلی روندهای متناهی بطور خودکار برای روندهای نامتناهی نیز معتبر خواهند بود. ’ قانون پیوستگی‘ نمونه‌ای از این موارد بود که ریاضیدان و فیلسوف آلمانی گاتفرید لایب‌نیتز (Gottfried Leibniz) در نامه‌ای که در سال 1702 به ریاضیدان فرانسوی پییر وارینون نوشت آن را اینطور خلاصه کرد: ” معلوم شده که قواعد متناهی در موارد نامتناهی نیز صدق می‌کنند“. ولی بعداً وقتی معلوم شد که در برخی موارد مفروضاتی از این نوع اشتباه هستند، دوره‌ای از سردرگمی فرا رسید. نهایتاً وقتی مفاهیم بطور منطقی تعریف شدند، خصوصیات لازم دقیقاً مشخص شدند، و این خصوصیات ثابت، یا رد، شدند، موضوع روشن شد.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

 

فصل 4

جنبه‌های فرعی بی‌نهایت

حالا ما توجه خودمان را از بی‌نهایتِ بزرگ به بی‌نهایتِ کوچک معطوف می‌کنیم. سه مثالی که در فصل 1 مطرح شد (قطر یک مربع، مساحت یک دایره، و نمایش کسر یک‌سوم بصورت اعشاری) نمونه‌هایی از این دست هستند. هر یک از آنها روندی را شرح می‌دهد که در آن یک شیء هندسی، یا یک عدد، بطور تکراری به اجزاء کوچکتری تقسیم می‌شوند، یا با ساختارهای بهتری به تقریب‌های دقیقتری می‌رسند، و اگر اینطور درنظر بگیریم که این روند بی‌نهایت بار تکرار می‌شود (یعنی هر یک اجزاء به اجزائی تقسیم می‌شود که طول آنها بی‌نهایت کوچک، یا اینفینی‌تسیمال، هستند)، آنگاه حاصل اینکار یک عدد کاملاً دقیق خواهد بود.

یونانیان باستان منطق‌دانان بسیار خوبی بودند، و متوجه شدند که اگر این روش به همین صورت بیان شود گمراه کننده است. ولی آنها برای معنی‌دار کردن آن روشی را یافتند که نام آن را  ِافنا (exhaustion) گذاشته بودند. وقتی طول‌های مورد نظر بخش‌ناپذیر بودند، اودوکسوس (Eudoxus) از این روش برای منطقی کردن پایه‌های نظریه تناسب استفاده کرد (که در واقع روشی برای روبرو شدن با اعداد غیرگویا بود، هرچند یونانی‌ها ترجیح می‌دادند در استدلال‌های خودشان بجای طول عددی، از طول خطوط استفاده کنند).

ما نگاه کوتاهی به روش افنا خواهیم انداخت و سپس از روش حسابان و مفهوم جدیدِ حد، که کار با بی‌نهایت کوچک‌ها را منسوخ کرد، استفاده خواهیم کرد. سپس به چگونگی مطرح شدن مجدد آنها می‌پردازیم.

اثبات قضیه ارشمیدس

ارشمیدس بطور صریح از π استفاده نمی‌کرد. در عوض او اثبات کرد که مساحت هر دایره برابر است با شعاع آن ضرب در نصف محیط. اگر ما π را بعنوان نسبت محیط به قطر دایره تعریف کنیم، این نتیجه برابر خواهد بود با πr². همانگونه که در فصل 1 نشان داده شد، می‌توان دایره را به برش‌های بسیار نازکی تقسیم کرد، و حدِ ’تعداد بینهایتی از برش‌های بسیار کوچک‘ را در نظر گرفت. ولی این رویکرد فاقد دقت است. در عوض ارشمیدس بر اساس دنباله‌ای از تخمینِ چندضلعی‌ها که مساحت و محیط‌های آنها مشخص بود، از روش افنا استفاده می‌کرد. یکی از دنباله‌ها دایره را از داخل، و دنباله دیگر آن را از خارج تخمین می‌زد.

فرض کنید A نشان دهنده حاصل‌ضرب شعاع ضرب در نصف محیط دایره باشد. آنگاه گزاره‌های زیر دو به دو از هم متمایز هستند و کلیه موارد ممکن را پوشش می‌دهند.

(1)  مساحت دایره بزرگتر از A است.

(2)  مساحت دایره کوچکتر از A است.

(3)  مساحت دایره مساوی A است.

این روش بجای اینکه سعی کند مستقیماً گزاره (3) را اثبات کند، با استفاده از برهان خلف ثابت می‌کند که هم (1) و هم (2) اشتباه هستند. بنابراین از نظر منطقی فقط (3) باقی می‌ماند.

دنباله ’خارجی‘ تخمینِ چندضلعی‌ها توسط یک شش‌ضلعی منظم محیط بر دایره تعریف می‌شود که مکرراً زاویه‌ها را نصف می‌کند تا چندضلعی‌های منظم 12، 24، 58، 96 ... ضلعی محیط بر دایره ایجاد کند. شکل (a)9 دو مرحله نخست این فرآیند، که تشکیل 6ضلعی و 12ضلعی است، را نشان می‌دهد (مراحل بعدی به قدری به دایره نزدیکند که ترسیم آنها در شکلی با این اندازه واضح نیست).

شکل 9. دو مرحله از تخمین یک دایره. (a) از خارج، (b) از داخل.

جزئیات رد گزاره (1) پیچیده‌ و طولانی‌اند، ولی ایده اصلی آن ساده است. اگر گزاره (1) درست باشد، در اینصورت مساحت دایره به اندازه d از A بزرگتر می‌شود (که d > 0 است). هر یک از چندضلعی‌های خارجی دارای مساحتی بیشتر از دایره هستند، بنابراین مساحت‌ آنها نیز از A+d بزرگتر است. ولی اگر تعداد اضلاع به اندازه کافی زیاد باشد، می‌توان ثابت کرد که مساحت چندضلعی کمتر از A+d است، و چنین تناقضی گزاره (1) را رد می‌کند. همانطور که در شکل (b)9 نشان داده شده، می‌توان از چندضلعی‌های ’درونی‘ استفاده کرد و با استدلال مشابه‌ای گزاره (2) را رد کرد. بنابراین تنها حالت ممکن گزاره (3) است.

مشکل عَمَلی که روش افنا دارد این است که شما باید از قبل جواب صحیح، یعنی A، را بدانید تا بتوانید حالت‌های سه‌گانه را مطرح کنید. مشکل نظری روش افنا این است که شما باید بدانید که آیا اصلاً کمیتی که بدنبال آن هستید وجود دارد یا نه. یونانیان فرض را بر این می‌گذاشتند که هر شکلی، خصوصاً دایره، دارای مساحت و محیطی است که بخوبی مشخص است. بعدها معلوم شد که چنین فرضی مستلزم وجود خصوصیاتِ ظریفِ آنالیزی است، ولی با اعمال دقت کافی، مساحت‌ و طول‌ بسیاری از اشکال (ولی نه همه آنها) را می‌توان تعریف کرد و خواص ملموسی از آنها را می‌توان اثبات نمود. ولی در زمانی که چنین چیزی معلوم شد، روش‌هایی پیدا شدند که از روش افنا بهتر بودند.

 

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

 

فصل 5

بی‌نهایتِ هندسی

اگر کنار یک خط آهن مستقیم و طولانی بایستید، یک حس قوی به شما می‌گوید که خطوط آهن یکدیگر را در افق قطع می‌کنند (شکل 12). دلیل آن هم این است که خطوط آهن با هم موازی هستند. در کناره‌های یک جاده مستقیم و طولانی نیز وضعیت به همین شکل است.

شکل 12. بنظر می‌رسد که خطوط راه‌آهن در افق همدیگر را قطع می‌کنند.

خطوط موازی در هندسه اقلیدسیِ عادی نقش خاصی را بازی می‌کنند. بر طبق تعریف، دو خط وقتی موازی هستند که همیشه فاصله آنها از هم یکی باشد، بنابراین هر چقدر هم که امتداد یابند نمی‌توانند همدیگر را قطع کنند. ولی اگر ناظری بر روی یک صفحه نامتناهی و میان دو خط موازی ایستاده باشد، آنگاه هرچقدر که دورتر برود، بنظر می‌رسد که این خطوط بهم نزدیکتر می‌شوند. به عبارت دیگر، بنظر می‌رسد این خطوط ’در بی‌نهایت‘ همدیگر را قطع می‌کنند- کشفی که باعث الهام دانش‌آموز گمنامی شد و ‌گفت: ”بی‌نهایت جایی است که چیزهایی اتفاق می‌افتند که نمی‌افتاند!“.

ریاضیدانان روشی یافته‌اند تا با اضافه کردن یک خط اضافی، که ’خط در بی‌نهایت‘ نام دارد و نشان دهنده افق است، هندسه اقلیدسی را توسعه دهند. خطوط عادی نیز بطور مشابه‌ای با اضافه کردن یک نقطه به آنها، که ’ نقطه در بی‌نهایت‘ نام دارد، بسط داده می‌شوند. این ایده به ایجاد نوع جدیدی از هندسه منجر شد که بسیار سودمند است و هندسه تصویری یا هندسه افکنشی (projective geometry) نام دارد. از لحاظ تاریخی، هنرهای بصری الهام‌بخش این هندسه‌ بودند. نقاشان ایتالیاییِ دوره رنسانس می‌خواستند اشیاء سه-‌بعدی را طوری ترسیم کنند که واقعی به نظر برسند.

نمای خطی (پرسپکتیو خطی)

همگرایی ظاهری خطوط موازیِ راه‌آهن یکی از ساده‌ترین نمونه‌هایِ نمای خطی یا پرسپکتیو خطی (Linear perspective) است. پرسپکتیو خطی عبارت است از نمایش دقیق اشکالِ هندسیِ سه-بعدی بر روی یک بوم مسطحِ دو-بعدی. در اینجا اشیائی که در دور‌دست هستند کوچکتر بنظر می‌رسند. شما می‌توانید با انگشت خودتان ماه را بپوشانید؛ اگر به گوسفندانی که در کشتزار هستند خیره شوید، آنها خیلی کوتاه‌تر از زمانی بنظر می‌رسند که از پشت حصار به آنها نگاه کنید. این تاثیرات بدلیلِ پیامدهای فیزیکِ پرتوهای نور و ساختار دستگاه بینایی انسان پدید می‌آیند. ولی این تاثیر به اندازه‌ای نیستند که باعث شود گوسفندانی که در جلو قرار دارند بزرگتر از آنهایی که در پشت هستند جلوه کنند. تمامی اجزاء هندسه نقاشی باید طوری به شکل نظام‌مند باهم جور شوند که به چشم ما اشیاء سه-بعدی را نشان دهند.

پیش از دوران رنسانس، نقاشان یا چنین چیزی را نادیده می‌گرفتند یا آن را اشتباه می‌کشیدند. برای مثال در نقاشی‌های مصر باستان، این مسئله نادیده گرفته می‌شد: مثلاً در نقش‌های برجسته، اندازه یک شخص عمدتاً به جایگاه اجتماعی او  بستگی داشت؛ خدمتکاران کوچکتر از اربابان خود هستند؛ زنان بیشتر اوقات (ولی نه همیشه) کوچکتر از شوهران خود هستند. در نقش برجسته‌ای که در شکل 13 دیده می‌شود، فرعون مصر رامسس دوم، بصورتی ترسیم شده که از اسبش بلندتر، و از بقیه آدم‌ها نیز خیلی بزرگتر است. در چنین مواردی هنرمند مجبور است در یک فضای محدود جزئیات فراوانی را بگنجاند. بویژه، استحکاماتی که در راست تصویر دیده می‌شوند کاملاً غیرواقعی هستند، و حالت پرسپکتیو ندارند. (البته چنین اظهاراتی را نباید انتقاد قلمداد کرد: مصریان خودشان بطور عمدی چنین سبکی را برگزیدند. در نقاشی‌های مصری، نقش‌های برجسته دیگری هم هستند که بطور قابل توجه‌ای واقعی بنظر می‌رسند، خصوصاً نقش پرندگان و بقیه موجودات زنده). برخی اوقات هنرمندان قرون وسطایی تلاش می‌کردند ساختمان‌ها را به شکل یک پرسپکتیو ابتدایی ترسیم کنند، ولی در ارتباط دادن منسجمِ آنها با یکدیگر ناکام بودند.

شکل 13. پیروزی رامسس دوم در نبرد داپور. برگرفته از یک نقش برجسته که در معبد او در تیبز قرار دارد.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

 

فصل 6

بی‌نهایتِ فیزیکی

امروزه بی‌نهایت به یکی از موضوعات اجتناب‌ناپذیر ریاضیات بدل شده، ولی بی‌نهایت یک وجودِ مفهومی است، و نه یک وجودِ واقعی. فیلسوفان درباره بی‌نهایت تفکر می‌کنند، و بحث می‌کنند که آیا وجود دارد یا نه، و اگر دارد، وجود آن به چه صورت است؟ در مذاهب مختلف، بی‌نهایت را غالباً یکی از صفات خدا یا خدایان می‌پندارند، و انسان‌ها برای انکار آن اعدام می‌‌شدند، ولی امروزه عموماً این اعتقاد رواج دارد که وجودِ خدا یک موضوع مذهبی است، نه یک دلیل عینی.

آیا بی‌نهایت خارج از ذهن انسان وجود دارد؟ آیا می‌تواند واقعی باشد، ولی نه به صورت یک اعتفاد مذهبی، بلکه به صورت چیزی ملموس مثل رودخانه، درخت، سنگ و غیره؟ گذشته از باریک‌بینی‌های فلسفی که لغاتی مانند ’واقعی‘ و ’وجود‘ در خود دارند، آیا کسی می‌تواند بی‌نهایت را به ما نشان دهد؟

تقریباً در تمام حوزه‌های علوم فیزیکی، یافتن جواب‌هایی که حاصل آنها بی‌نهایت باشند مایه شرمساری است. نظریه‌ای که کمیت‌های بی‌نهایت را پیش‌بینی کند، اشتباه است. این به این معنی نیست که چنین نظریه‌ای به‌ درد نمی‌خورد، بلکه به تعدیل‌هایی نیاز دارد که از شر آن بی‌نهایت‌های مزاحم خلاص شود. ولی در یکی از حوزه‌های فیزیک، وجود بی‌نهایت نه تنها تحمل می‌شود، بلکه به عنوان یک حقیقتِ ممکن در نظر گرفته می‌شود؛ این حوزه کیهان‌شناسی (cosmology) نام دارد.

بحث را با فیزیک نظری شروع می‌کنم، که در آنجا سر و کله بی‌نهایت بصورت عادی پیدا می‌شود. در اینجا از یک کمیت‌ بی‌نهایت تحت عنوان تکینگی‌ (singularity) نام برده می‌شود، و حضور آن نشانه‌ای از معیوب بودن مدل است. ولی جدا از وجود تکینگی‌ها، این نظریه‌ها می‌توانند بسیار دقیق باشند. من موضوع تکینگی را در سه زمینه بررسی می‌کنم: نورشناسی، گرانشِ نیوتونی، و نسبیت اینشتین. سپس بطور اجمالی به این موضوع می‌پردازیم که آیا جهان متناهی است یا نه.

بی‌نهایت در نور شناسی

بسیاری از جلوه‌های باشکوه طبیعت توسط تاثیرات غیرعادی ایجاد می‌شوند که نور در آنها دخیل است. آشناترین آنها رنگین‌کمان است، که بصورت یک کمان باریکِ چند رنگی در طول آسمان ظاهر می‌شود. نمونه دیگر هالهِ نور است، که در آن شخصی که پشت سر او خورشید قرار دارد و به مه خیره شده در بالا سر سایه خودش نور رنگین‌کمان شکلی را می‌بیند. کسی که در کنار او قرار دارد نیز هم چیز را می‌بیند، ولی حالا نور دور سر خودش دیده می‌شود. ممکن است سنت پیدا شدن حلقه‌های نورانی در بالای سر قدیسین نیز از پدیده هالهِ نور ناشی شده باشد، که قدمت آن حداقل به قرن اول بازمی‌گردد و در میان بوداییان رواج داشته. برخی اوقات حلقه‌های کامل هاله مانند به دور خورشید یا ماه نیز دیده می‌شوند، که همراه با تاثیرات نادری مثل ستون‌های نوری و پراخورشید (parhelion) هستند.

چنین تاثیراتی هنگامی روی می‌دهند که نور خورشید بوسیله قطرات آب یا بلورهای یخ منعکس و یا خم می‌شوند. رنگین‌کمان هنگامی ظاهر می‌شود که خورشید پشت سر ناظر قرار دارد و در جلو او از ابرها باران می‌بارد. نور خورشید با قطرات باران برخورد کرده و شکسته می‌شود، سپس از پشت قطره منعکس می‌شود، و نهایتاً به سمتی دیگر شکسته می‌شود (شکل 26). شعاع زاویه‌ای رنگین‌کمان در حدود 42.5 درجه است، و رنگ‌های آن بر اساس طول‌موج‌ مرتب شده‌اند. معمولاً یک رنگین‌کمانِ کم‌رنگ‌تر نیز دیده می‌شود‌ که خارج از رنگین‌کمان اصلی قرار دارد، و در اثر شکست‌ها و انعکاس‌های بیشتر پدید آمده، و شعاع زاویه‌ای آن در حدود 52 درجه است. هاله نور نیز به طور مشابه‌ای در اثر عبور نور خورشید در داخل قطرات مه ایجاد می‌شود، ولی به دلایل فیزیکی پیچیده، تقریباً مسیر خودش را معکوس می‌کند، و به همین دلیل است که بنظر می‌رسد از سایه سرِ ناظر ساطع می‌شود. این شامل یک سری از حلقه‌های رنگی پیچیده است که روشنایی‌های مختلفی دارند. هاله‌هایی که در اطراف خورشید و یا در اطراف ماه ظاهر می‌شوند، هر دو توسط بلورهایی پدید می‌آیند که در اتمسفر بالایی قرار دارند. ساده‌ترین نوع آنها حلقه‌ای است که شعاع زاویه‌ای آن در حدود 22 درجه است، و دلیل آن هندسهِ خاصِ بلورهای یخ است.

شکل 26. انحراف D(α) در زاویه نوری که به یک قطره کروی آب (باران) برخورد می‌کند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

 

 

فصل 7

بی‌نهایتِ شمارشی

از نظر من مهمترین کشفی که درباره بی‌نهایت صورت گرفت، یعنی همان چیزی که همه فیلسوفان (و همه ریاضیدانان پیشین) آن را از قلم انداخته بودند، کشفی بود که در سال 1874 توسط گئورگ کانتور (Georg Cantor) صورت گرفت. او بصورت منطقی و بادقت نشان داد که حتی در قلمرو اعداد نیز، بی‌نهایت می‌تواند اندازه‌های مختلفی داشته باشد. خصوصاً نامتناهی بودن اعداد حقیقی، بزرگتر از اعداد طبیعی (یعنی اعداد 1, 2, 3, …) است. منظور او صرفاً این نبود که برخی از اعداد حقیقی اعداد طبیعی نیستند، که البته موضوعی درست و بدیهی است. اثبات او نشان داد که غیر ممکن است بتوان کلیه اعداد حقیقی را با اعداد طبیعی متناظر کرد، بصورتی که هر عدد حقیقیِ متمایز، با یک عدد طبیعیِ متمایز متناظر شوند. اعداد طبیعی نامتناهی ولی شمارش‌پذیرند، درحالی که اعداد حقیقی علاوه بر اینکه نامتناهی هستند، شمارش‌ناپذیر نیز هستند.

کانتور در سال 1891 به این قضیه بازگشت، و برای آن اثبات متفاوتی ارائه داد، که به ’استدلال قطری کانتور‘ معروف است و من بعداً آن را توضیح خواهم داد. ولی در سال 1874 او به دنبال اثبات متداولتری بود. از قرن هفدهم به بعد، ریاضیدانان میان اعداد جبری (algebraic numbers)، و غیرجبری یا متعالی (transcendental numbers) تمایز قایل شده بودند. اعداد جبری اعدادی هستند که می‌توانند جواب یک معادله چندجمله‌ای با ضرایب صحیح باشند، و اعداد غیرجبری هم اعدادی هستند که این خاصیت را ندارند. ریاضیدانان بطور گسترده بر این باور بودند که اعدادی مثل e و π غیرجبری هستند، ولی اثبات این مسئله دشوار بود و مدتها طول کشید تا ثابت شود. در واقع زمانی بود که حتی نمی‌دانستند که اعداد غیرجبری وجود دارند یا نه. ریاضیدان فرانسوی جوزف لیوویل (Joseph Liouville) ثابت کرد که چنین اعدادی وجود دارند، ولی این اثبات بر اساس ساختِ صریحِ اعدادی بود که به برآورد یک عدد غیرجبری منتهی می‌شد. کانتور بدون اینکه به ساخت چنین اعدادی بپردازد، اثبات کرد که آنها وجود دارند.

بکارگیری این روش باعث شد کانتور به سمت نظریه‌ای برای مفهوم عدد هدایت شود، که او آن را (Mengenlehre) ، یا نظریه گردایه‌ها، می‌نامید. حالا این به نظریه مجموعه‌ها (set theory) معروف است. کارهایی که او بر روی این نظریه انجام داد عمدتاً میان سال‌های 1874 تا 1884 منتشر شدند. این کارها حاصل یک قرن تلاش برای تعریفِ دقیقِ ’عدد‘ بصورت منطقی بود، و پایه‌های منطقی تمامِ ریاضیات را فراهم آوردند. ولی نظریه مجموعه‌ها چنان اساسی است که مفاهیم مطرح در آن به سختی به ریاضیات شباهت دارند، و مطمئناً در زمان کانتور نیز اینطور بنظر می‌رسید. نظریه مجموعه‌ها انتزاعی است، و برای کسانی که با سُنتِ ریاضیات قرنِ نوزدهم پرورش یافته بودند، ناملموس بنظر می‌آمد. کانتور نسبت به این مشکل آگاه بود، و آن را اینطور شرح می‌دهد: ”من متوجه شده‌ام که خودم را در جایگاه خاصی قرار داده‌ام که با دیدگاه‌ قالب درباره بی‌نهایت ریاضی، و با عقایدی که درباره سرشت اعداد وجود دارد، در تضاد است.“

عقاید کانتور برای بسیاری انقلابی بودند؛ چند تن از ریاضیدانان برجسته با عباراتی که قالباً تند بود، ایده‌های او را مهمل شمرده و آنها رد کردند. شخصیت پرنفوذی مانند لئونارد کرونکر (Leopold Kronecker)، بصورت علنی کانتور را یک شیاد علمی، یک مرتد، و گمراه کنند جوانان نامید. ولی جالب است که خود کرونکر نیز از جمله کسانی بود که عقاید خاصی داشت؛ او یک متخصص اعداد بود که نسبت به آنچه در ریاضیات مجاز است دیدگاه‌های افراطی داشت، و نقل قول معروفی از او هست که می‌گوید ”خدا اعداد صحیح را آفرید، بقیه کار انسان است.“  امروزه هیچ جنبه‌ای از ریاضیات نیست که به عنوان یک موهبت خدا-دادی به آن نگاه شود، و مشکلات منطقی که بنیانِ ریاضیات به آن دچار است، قبلاً گریبان اعداد صحیح را نیز گرفته. اگر ریاضیاتِ اعدادِ صحیح بطور منطقی سازگار و غیر-متناقض باشد، آنگاه برای اعداد حقیقی، اعداد مختلط، و به‌ویژه نظریه مجموعه‌ها، نیز همین‌طور خواهد بود.

حتی در زمان کانتور نیز خیلی از ریاضیدانان آنقدر بصیرت داشتند که به اهمیت اختراع او پی ببرند. برجسته‌ترین آنها ریاضیدان آلمانی داوید هیلبرت (David Hilbert) بود، که گفته بود: ”هیچ کس نمی‌تواند ما را از بهشتی که کانتور برای ما آفریده بیرون براند.“ بالاخره استدلال کانتور برنده این بازی شد، ولی زمانی این اتفاق افتاد که او مرده بود. او از سال 1904 به بعد به بیماری افسردگی مزمن دچار شده بود، و سرانجام در سال 1918 در یک آسایشگاه روانی فوت کرد.

شمارش و تطبیق

جاده‌ای که به بهشت کانتور ختم می‌شود با راهی آغاز می‌شود که ما برای یافتن تعداد چیزها از آن استفاده می‌کنیم. این راه شمارش (Counting) نام دارد (شکل 30). چوپانی که یک گله کوچک گوسفند دارد به ترتیب به آنها اشاره می‌کند و می‌گوید ’یک، دو، سه، چهار، پنج، شش، هفت‘. وقتی گوسفندی باقی نماند، و چوپان هم دقت کرده باشد تا هر یک از آنها را دو بار نشمرده باشد، او نتیجه می‌گیرد که هفت گوسفند دارد.

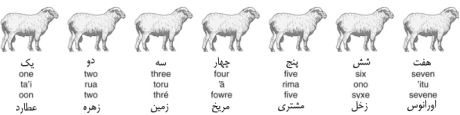
شکل 30. شمارش گوسفندان به چهار زبان مختلف و تناظر آنها با نام سیارات منظومه شمسی.

یک چوپان انگلیسی که با چنین کاری و چنین گله‌ای روبر باشد، او نیز گوسفندان خود را می‌شمارد، ولی خواندن او متفاوت خواهد بود: ’one, two, three, four, five, six, seven ‘، و خواهد گفت که seven گوسفند دارد.

چوپانی که در زلاند نو زندگی می‌کند، و با چنین کاری و چنین گله‌ای روبر باشد، او نیز گوسفندان خود را می‌شمارد، ولی خواندن او نیز متفاوت خواهد بود: ’ta’i, rua, toru, ’ā, rima, ono, ’itu ‘، و خواهد گفت که ’itu گوسفند دارد.

و به همین ترتیب برای زبان‌های دیگر.

اینجا هیچ اختلاف نظری وجود ندارد، تنها چیزی که هست نام‌های مختلف برای یک چیز است. یک اخترشناس ممکن است گوسفندان را با خواندن آنها بصورت ’عطارد، زهره، زمین، مریخ، مشتری، ذحل، اورانوس‘ بشمارد.

حالا فرض کنید که به همه گوسفندان دقیقاً یک زنگوله بسته باشند، در اینجا چه تعداد زنگوله وجود دارد؟ در اینحالت کسی زحمت شمارش مجدد را به خودش نمی‌دهد، و فوری جواب می‌دهد ’هفت!‘، یا ’Seven!‘، یا ’Itu!‘، یا ’اورانوس!‘.  اعداد (یعنی همانجایی که آواز خواندن چوپان متوقف شده) نیز همینطور هستند. چرا؟ زیرا هر عدد با یک گوسفند تطبیق دارد، هر گوسفند نیز با یک زنگوله؛ بنابراین هر عدد با یک زنگوله تطبیق دارد. نامی که ریاضیدانان در گذشته به این روند داده بودند تناظر یک-به-یک (one-to-one correspondence) بود. چون این نام کمی طولانی و دهان‌پرکن بود، پس امروزه بجای آن، به دانش‌آموزان مجموعه‌های منطبق با هم را یاد می‌دهند، به امید اینکه به آنها کمک کنند تا اعداد را بهتر درک کنند. ریاضیدانان این روند را دو سویه (bijection) یا یک نگاشت یک-به-یک و پوشا می‌نامند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.