ترجمههای کامران بزرگزاد

مقدمهای بر
سایفرها و جایگزینی
توضیح برخی
اصطلاحات و بررسی سایفر سِزار
1.5- تحلیل رمز
سایفرهای جایگزینی ساده. 11
1.6- سایفرهای
جایگزینی چندنگاری
1.7- حملات متن
غیررمزی-شناختهشده
4.1- سایفرهای
چندلفظی و اعداد باینری.. 19
6.1- رمزگذاری
با استفاده از توان
7.1- ایده اولیه
سایفرهای کلید-عمومی
انواع دیگر
سیستمهای کلید-عمومی
رمزنگاری
از قدیمیترین علوم است که قدمت آن به حدود 3000 سال قبل بازمیگردد. همیشه از
دیرباز برخی از مردم میخواستهاند طوری با یکدیگر ارتباط برقرار کنند که اشخاص
نامحرم از صحبتهای آنها چیزی متوجه نشوند، و به همین منظور روشهای مختلفی را
برای مخفی نگاه داشتن ارتباطات خودشان ابداع کردهاند. در ابتدا رمزنگاری بیشتر بر
نوشتن تکیه داشت، هرچند به آن محدود نبود.
تعداد
کتابهایی که درباره رمزنگاری به فارسی منتشر شده به تعداد انگشتان یک دست هم نیست.
مدتها بود که قصد داشتم کتابی را در این زمینه ترجمه کند، ولی اینکه این کتاب در
چه سطحی، و مخاطبین آن چه کسانی باشد تردید داشتم. نهایتاً وقتی این کتاب را دیدم،
محتوا و شیوه بیان آن را مناسب تشخیص دادم و تصمیم به ترجمه آن گرفتم. نام اصلی
کتاب ”The mathematics of secrets“ یا ”ریاضیات اسرّار“ است. کتاب در رده
مقدماتی طبقه بندی میشود و دانشجویان رشتههای کامپیوتر، ریاضیات، الکترونیک و مخابرات،
و کلاً علاقمندان این حوزه میتوانند از آن استفاده کنند. قسمت قابل ملاحظهای از
این کتاب شامل تاریخ رمزنگاری است، که سیر تاریخی این علم را از عهد یونان باستان تا به
امروز، که در عصر
پسا-کوانتومی بسر میبریم، مرور میکند. کتاب کار خودش را با سادهترین
و قدیمیترین نوع رمزنگاری، که رمزنگاری جانشینی نامیده میشود، شروع کرده و در
فصول آخر جدیدترین تکنیکهای رمزنگاری نوین، که شامل رمزنگاری منحنی بیضوی و رمزنگاریهای کوانتوم-پایه
است، را نیز توضیح میدهد.
مطالعه
این کتاب به غیر از ریاضیات دبیرستانی پیش نیاز دیگری ندارد. اصولاً از اواخر قرن
نوزدهم به بعد، پایه اصلی علم رمزنگاری را ریاضیات، و اگر دقیقتر بگوییم عمدتاً
نظریه اعداد، تشکیل میدهد. ولی ریاضیاتی که در رمزنگاری مقدماتی از آن استفاده میشود
خیلی پیچیده نیست، و همانطور که اشاره شد با داشتن مهارتهای ریاضی دبیرستان میتوان
بخوبی آن را درک کرد. مفاهیمی همچون حساب پیمانهای، جایگشتها، و حل معادلات چند
مجهوله، چیزهای هستند که همه دانشجویان سالهای اول رشتههای فنی و مهندسی با آنها
آشنایی دارند. البته هنگامی که صحبت بر سر تکنیکهایی مثل منحنیهای بیضوی، یا
حساب کوانتومی باشد، اینها مواردی هستند که حقیقتاً پیشرفته هستند، ولی حتی چنین
مباحثی نیز در این کتاب از قلم نیافتاده و توضیحات مقدماتی درباره آنها ذکر شده
است.
اصولاً
منظور از رمزنگاری نوین، تکنیکها و روشهایی است که در قرن بیستم، و خصوصاً پس از
جنگ جهانی دوم، ابداع شدهاند. هرچند در قرون وسطی در شمال آفریقا و خاورمیانه
نشانههایی از رمزنگاری دیده میشود، ولی آنچه رمزنگاری نوین نامیده میشود سابقه
زیادی در ایران ندارد. تا پیش از دهه هفتاد شمسی، کاربرد رمزنگاری در ایران عمدتاً
به کاربردهای نظامی و دیپلماتیک محدود بود، ولی حتی این کاربردها نیز بیشتر بر روی
استفاده از کلمات و جملات رمزی، و کلاً استفاده از کُد (Code)
محدود بودند. حتی در جنگ هشت ساله ایران و عراق، در عملیات نظامی بیشتر از کلمات
رمزی استفاده میشد، و ارتباطات واحدهای کوچک نظامی یا اصلاً مخفی نبود، یا اگر هم
مخفی بود با کلمات رمزی صورت میگرفت. البته در سطح واحدهای بزرگ نظامی، مثل
ستادهای عملیاتی، از نوع رمزنگاری استفاده میشد، ولی حتی آنهم جزء چیزهایی نبود
که بتوان آن را بخشی از رمزنگاری نوین بحساب آورد. اصولاً رمزنگاری نوین وابسته به
کامپیوتر و مخابرات دیجیتال است، و این چیزی نبود که در دوران جنگ هشت ساله، یا
قبل از آن، بطور گسترده در دسترس باشد. تنها پس از دوران جنگ و در اواخر دهه شصت
شمسی بود که با ظهور گسترده کامپیوترهای کوچک، استفاده از تکنیکهای رمزنگاری نوین
و مخابرات دیجیتال میسر شد. در حال حاضر اینترنت بصورت جزء جدا نشدنی زندگی بیشتر
انسانها درآمده، و یکی از پایههای اینترنت را رمزنگاری تشکیل میدهد. امروزه هر
مهندس نرمافزار و سختافزار، یا مخابرات باید از مبانی و کاربردهای رمزنگاری نوین
مطلع باشد. در این میان دانشجویان ایرانی هم استثنا نیستند. در اواسط دهه 1380 یک
نهاد دولتی بنام انجمن رمز ایران تاسیس شد که هدف آن پیشبرد و توسعه
رمزنگاری در ایران است. اساتید و دانشجویان زیادی در این نهاد عضو هستند، و این
نوید دهنده یک آینده خوب برای رمزنگاری در ایران است.
جاشوا
هولدن (Joshua Holden) در سال 1970 بدنیا
آمد و در حال حاضر استاد ریاضی دانشگاه پرینستون آمریکا است. گرایش اصلی هولدن
نظریه اعداد و رمزنگاری است. او از کارشناسان شناخته شده این حوزه است و تاکنون در
کنفرانسهای متعدد بینالمللی دراینباره سخنرانی کرده است.
تابستان 1396
کامران بزرگزاد
این کتاب
مبانی ریاضی رمزنگاری (cryptography)، یا بعبارتی اساس
فرستادن پیامهای سرّی را شرح میدهد. رمزنگاری نوین یک علم است و مانند
بقیه علوم نوین بر ریاضیات تکیه دارد. بدون استفاده از ریاضیات حداکثر جایی که شما
میتوانید به آن برسید فقط کسب نوعی بینش مقدماتی از رمزنگاری است. ولی من میخواهم
شما قادر باشید که از این فراتر قدم بردارید. دلیل آن هم تنها این نیست که شما
باید از جزئیات ریاضی مربوط به رمزنگاری مطلع باشید، بلکه من تصور میکنم ریاضیاتِ
خاصی که در پشت رمزنگاری نهفته شده حقیقتاً زیبا است و من قصد دارم در این کتاب آن
را به شما معرفی کنم.
در کتابی
که فیزیکدان معروف استیون هاوکینگ (Stephen Hawking)، بنام تاریخچه مختصر زمان
نوشت، او میگوید شخصی به وی توصیه کرده که هر معادلهای که در کتابش بگنجاند موجب
میشود فروش کتاب نصف شود، بنابراین باید از آوردن معادلات در کتاب پرهیز کند. من
امیدوارم چنین چیزی در مورد این کتاب صادق نباشد، زیرا معادلات زیادی در این کتاب
خواهند آمد. ولی فکر نمیکنم ریاضیات مربوط به این معادلات لزوماً دشوار باشد.
برای توضیح بیشتر مفاهیم ریاضی این کتاب جبر دبیرستانی کفایت میکند. البته عامل
مهمی که در یادگیری این کتاب تاثیر دارد اشتیاق به یادگیری مفاهیم است. در اینجا
نه خبری از مثلثات هست، نه حسابان، و نه معادلات دیفرانسیل. در این کتاب ایدههایی
خواهند آمد که معمولاً در کلاسهای جبر معمولی مطرح نمیشوند، و من تلاش خواهم کرد
تا آنها را برایتان روشن کنم. اگر شما حقیقتاً میخواهید این ایدهها را یاد
بگیرید، میتوانید بدون گذراندن هیچ دوره ریاضی دانشگاهی اینکار را انجام دهید،
ولی شرط آن این است که خوب توجه کنید. ریاضیاتی که در برخی از ستونهای کناری مطرح
میشود ممکن است کمی سختتر باشد، ولی شما میتوانید از آنها صرف نظر کنید. ادامه
یادگیری مطالب بعدی کتاب به آنها بستگی ندارد.
کُل
رمزنگاری در ریاضیات خلاصه نشده. برخلاف بیشتر علوم دیگر، رمزنگاری در مورد
حریفانِ زیرکی است که در مورد حفظ اسرار خود بطور فعال با یکدیگر در حال نبرد
هستند. یان کَسلز
(Ian
Cassels) که یک ریاضیدان برجسته، و یکی از رمزنگاران درگیر در جنگ جهانی دوم بود، نظر
جالبی در مورد رمزنگاری دارد. او میگفت: ”رمزنگاری مخلوطی از ریاضیات و آشفتگی
است، اگر آشفتگی وجود نداشته باشد، میتوان از خودِ ریاضیات برعلیه رمزنگاری
استفاده کرد.“ من در این کتاب زیاد به این آشفتگیها نپرداختهام و بیشتر تمرکزم را بر روی
ریاضیات گذاشتهام. برخی از رمزنگاران حرفهای ممکن است با رویکردی که من اتخاذ
کردهام موافق نباشند، دلیل آن هم این است که حقیقتاً من در این کتاب امنترین روشهای
رمزگذاری را به شما نشان نمیدهم. در پاسخ به این انتقاد، تنها میتوانم بگویم که
این کتاب تنها برای آن دسته از افرادی نگاشته شده که مایلند بخشی خاصی از رمز
نگاری را یادبگیرند، آن بخش خاص هم مبانی ریاضی رمزنگاری است. برای یادگیری
رمزنگاری کتابهای خیلی زیادی وجود دارند، و اگر میخواهید یک رمزنگار حرفهای
شوید، باید برخی از آنها را مطالعه کنید.
لازم است
برخی از خطوطی که در نگارش این کتاب رعایت شده را روشن کنم: من برای اینکه مفاهیم
را سادهتر کنم، چیز دروغی را در این کتاب نیاوردهام. من از مطرح کردن برخی از
جزئیات مربوط به ایمنتر کردن سیستمها صرفنظر کردهام. همچنین برخی سیستمهایی
که تصور میکنم نقش زیادی در جنبههای ریاضی رمزنگاری ندارند را نیز از قلم
انداختهام. تا آنجا که ممکن بوده سعی کردم سیستمهایی را معرفی کنم که حقیقتاً
برای حفظ اسرار کاربرد دارند. ولی در جاهایی که احساس کردم نیاز به توضیحات
بیشتری است، سیستمهایی را نیز در این کتاب گنجاندهام که توسط افراد دانشگاهی مثل
خودم و دیگران ساخته شدهاند.
تکنولوژی
کامپیوتر، هم از نظر دادههایی که رمزنگاران با آن کار میکنند و هم از نظر تکنیکها،
تغییرات زیادی کرده. برخی از سیستمهایی که من در این کتاب به آنها اشاره کردهام،
امروزه دیگر کاربرد ندارند، یا اینکه حتی اگر در گذشته امن بودهاند، امروز امن
بحساب نمیآیند. به همین ترتیب برخی از تکنیکهایی که من برای شکستن این سیستمها
به آنها اشاره میکنم امروزه دیگر تاثیر گذشته خود را ندارند. با این وجود تصور میکنم
کلیه موضوعاتی که در این کتاب مطرح شدهاند نشان دهنده مباحثی هستند که هنوز هم
مهماند و به رمزنگاری نوین وابستگیهای زیادی دارند. حتی اگر سیستمهای مورد
اشاره در این کتاب کاربرد خودشان را هم از دست داشته باشند، تلاش من بر این بوده
که نشان دهم اصول مطرح شده در کتاب هنوز هم در رمزنگاری نوین پابرجا هستند.
بخشهایی که در پایان هر فصل تحت عنوان ”نگاهی بجلو“ میآیند، به شما نشان خواهد که
فصلی که آن را به اتمام رساندید چگونه با فصول آتی، یا مباحث بعدی، ارتباط دارد.
بسیاری از
فصول کتاب پیشرفت تاریخی موضوعاتِ مطرح شده را دنبال میکنند، زیرا غالباً چنین
پیشرفتی حاصل برآیند منطقیِ توسعه ایدههایی است که آنها را شرح میدهم. همچنین
تاریخ روش خوبی برای بیان داستان است، بنابراین من دوست دارم در جاهایی که مناسب
باشد از این روش استفاده کنم. مطالب بسیار بیشتری درمورد تاریخ رمزنگاری وجود
دارد، بنابراین اگر مایلید آنها را بدانید حتماً به بخش منابع برای مطالعات
بیشتر رجوع کنید.
من همیشه
به دانشجویانم میگویم دلیلی که استاد ریاضی شدم این بود که هم به ریاضیات علاقه
داشتم و هم به حرف زدن. این کتاب هم برای من وسیلهای است که با شما حرف بزنم، حرف
زدن درباره کاربردِ ریاضیاتی که حقیقتاً آن را دوست دارم. امید من این است که در
پایان این کتاب شما نیز چنین ریاضیاتی را دوست داشته باشید.
تقریباً از
همان ابتدایی که نوشتن اختراع شد، انسانها سعی داشتند تا محتوای برخی از نوشتههای
خود را پنهان کنند، و برای انجام اینکار روشهای مختلفی را نیز ابداع کردند. درست
در همان زمانی که مردم شروع به پنهان کردن پیامهای خود کردند، محققانی نیز پیدا
شدند که شروع به شرح و دستهبندی این روشها نمودند. متاسفانه مجبورم برای روشنتر
شدن موضوع اصطلاحات زیادی را برای شما تشریح کنم. حتی بدتر از این، اصطلاحاتی وجود
دارند که در مکالمات روزمره معمولی کاملاً جا افتادهاند ولی برای کارشناسان این
حوزه معانی متفاوتی دارند،
هرچند فهم این معانی چندان سخت نیست.
بعنوان
مثال، کسانی که در کار رمزنگاری هستند اغلب از دو کلمه سایفر (cipher) و کُد (code)
برای دو چیز متفاوت استفاده میکنند. دیوید کان (David Kahn)،
که شاید بتوان از او بعنوان مؤلف مهمترین کتاب تاریخ رمزنگاری یاد کرد، میگوید: ”یک
کُد شامل هزاران لغت، عبارت، حرف، و هجا است، که بهمراه کُدواژهها (codewords) جایگزین این عناصر در متنهای غیررمزی میشوند ... از
سوی دیگر، واحد اصلی در سایفر حرف است، برخی اوقات نیز جفتی از حروف ... یا بندرت
گروههای بزرگتری از حروف ...“. علاوه بر سایفر و کد، روش سومی نیز برای فرستادن
پیامهای سری وجود دارد که پنهاننگاری (steganography)
نام دارد، و در آن سعی میشود با استفاده از روشهایی، مثل جوهر نامریی، اصل پیام
پنهان شود. در این کتاب ما تمرکز خودمان را بر روی سایفرها خواهیم گذاشت، زیرا
آنها هستند که عموماً از لحاظ ریاضی جالبترند، گرچه نمونههایی از روشهای دیگر را
نیز ذکر میکنیم.
پیش از
اینکه کار خودمان را شروع کنیم، توضیح برخی از اصطلاحات دیگر نیز مفید خواهد بود.
مطالعه چگونگی فرستادن پیامهای سرّی توسط کُدها و سایفرها، رمزنگاری (cryptography) نام دارد، درحالی که چگونگی
خواندن این پیامهای سرّی، آنهم بدون داشتن اجازه،
تحلیلرمز (cryptanalysis) یا رمزشکنی (codebreaking)
نامیده میشود. (برخی اوقات از واژه رمزنگاری برای ترکیب این دو حوزه با هم
استفاده میشود، ولی ما باید این اصطلاحات را از هم جدا نگاه داریم).
غالباً در
رمزنگاری معمول است که از فرستنده پیام بعنوان آلیس (Alice)، از گیرنده پیام بعنوان باب (Bob)، و از کسی که بطور
مخفیانه به پیامهای رد و بدل شده میان آلیس و باب گوش میدهد، بعنوان ایو
(Eve) نام برده میشود.
در این
کتاب ما کار خودمان را با جولیوس شروع میکنیم، که نام کوچک جولیوس سِزار (Julius Caesar) است. سزار علاوه بر
داشتن عنوان دیکتاتورِ روم، یک نابغه نظامی، یک نویسنده، و ... یک رمزنگار نیز
بود.
شاید
مخترع اصلی آنچه ما امروز بنام سایفرِ سزار میشناسیم خود سزار نباشد، ولی
مطمئناً او بود که باعث محبوبیت آن شد. تاریخنگار رومی Suetonius سایفر سِزار را چنین
توصیف میکند:
از سزار نامههایی بجا مانده که او به دولتمرد رومی
سیسِرو (Cicero)،
و همچنین دوستان صمیمی خود نوشته، او هنگامی که میخواسته مطالب محرمانهای را
مطرح کند، آنها را بصورت رمزی مینوشته. او اینکار را با تغییر ترتیب حروف الفبا
انجام میداده، بصورتی که کلمات قابل فهم نباشند. اگر کسی میخواست آنها را بفهمد
و معنی آنها را درک کند، باید حروف را با سه حرف قبل خود جایگزین میکرد، مثلاً D را با A، و غیره.
بعبارت
دیگر، هر موقع آلیس میخواست پیامی را بفرستد، او ابتدا متن غیررمزی (plaintext) خود را به زبان
معمولی مینوشت. سپس با استفاده از یک سایفر این پیام را رمزگذاری (encipher) میکرد، نتیجه
اینکار چیزی بود که متنرمزی (ciphertext) پیام نامیده میشود.
از لغت encode
میتوان برای به کُد در آوردن پیام، و همچنین از لغت encrypt
میتوان برای هر دو آنها (encipher
و encode)
استفاده کرد.
برای
مثال، آلیس (یعنی فرستنده پیام) کلیه aهایی را که در متن غیررمزی وجود دارند، در
متنرمزی با D
جایگزین میکند، و برای bها، آنها را با E جایگزین میکند، و الی آخر.
هر حرف به اندازه 3 حرف به جلو انتقال داده میشود.
اینکار کاملاً واضح است. بخش جالب کار وقتی است که آلیس به حرف آخر الفبا برسد و
دیگر حرفی برای او نماند که به جلو برود. اگر حرف w با Z جایگزین شود، پس تکلیف حرف
بعدی، یعنی x، چه میشود؟ این حرف
به A باز میگردد! حرف y، با B جایگزین میشود، و z با C. برای مثال، با استفاده از
این روش پیام ”and you too, Brutus“
به متنرمزی زیر بدل میشود:
متن غیررمزی:
a n d y o u t o o b r u t u s
متن رمزی : D Q G B R X W R R E U X W X V
این پیامی
است که آلیس به باب (یعنی گیرنده پیام) میفرستد.
شما نیز
از دوران کودکی خود با ایده ” بازگشت به ابتدا“ آشنا بودهاید و از آن استفاده میکردهاید.
در ریاضیات ابتدایی سؤالاتی مثل این پرسیده میشوند: سه ساعت بعد از ساعت 1 چه
ساعتی است؟ پاسخ ساعت 4 است. سه ساعت بعد از ساعت 2 چه ساعتی است؟ ساعت 5. سه ساعت
بعد از ساعت 10 چه ساعتی است؟ ساعت 1. در مورد آخر، کاری که شما انجام میدهید
همان بازگشت به ابتدا (wraparound) است.
در اوایل
قرن نوزدهم میلادی بود که کارل
فردریش گاوس (Carl Friedrich Gaus)
بازگشت به ابتدا را بصورت یک ایده ریاضی مطرح کرد. حالا ما به آن حساب پیمانهای (modular arithmetic) میگوییم، و عددی که
به آن باز میگردیم هم پیمانه (modulus) نام دارد. یک
ریاضیدان مسئله ”سه ساعت بعد از ساعت 10“ را به شکل زیر مینویسد:
10 + 3 ≡ 1 (12 به
پیمانه)
و آنرا
اینطور میخوانیم ”10
به اضافه 3،
به پیمانه 12 برابر 1 است.“
ولی تکلیف
این بازگشت به ابتدا برای سایفر سزار چه میشود؟ اگر ما بخواهیم حروف را به
اعداد تغییر دهیم، میتوانیم برای نمایش این بازگشت از حساب پیمانهای استفاده
کنیم. مثلاً بجای حرف a
از عدد 1، بجای حرف b
از عدد 2، و غیره استفاده میکنیم. در واقع این تبدیل حروف به
اعداد، بخشی از رمزی کردن پیام محسوب نمیشود. برای افراد باهوشی مثل ما، چنین
چیزی کاملاً ساده و آشکار است، و آلیس نباید انتظار داشته باشد آن را بعنوان یک
چیز سّری قلمداد کند. چیزی که سّری قلمداد میشود آن عملیاتی است که ما بر روی این
اعداد انجام میدهیم.
در اینجا پیمانه ما 26 است و سایفر سِزار به
شکل زیر درمیآید:
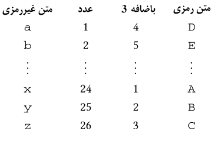
بخاطر
داشته باشید که وقتی ستون ”به اضافه 3“ به 26 رسید، دوباره به ابتدا باز میگردد.
برای رمزگشایی (decipher)، یا بعبارتی تبدیل
متنرمزی به متن غیررمزی، باب باید حروف را به اندازه سه حرف در جهت مخالف، یعنی
به سمت چپ، انتقال دهد. اینبار هنگامی که او به ابتدا رسید باید به انتها بازگشت
کند، یا اگر بخواهیم بصورت عددی بگوییم، هنگامی که به 0 رسید، آن را با 26
جایگزین کند، به -1 که رسید آن را با 25
جایگزین کند، و غیره. اگر از جدولی مانند آنچه قبلاً دیدیم استفاده کنیم، رمزگشایی
بصورت زیر خواهد بود:
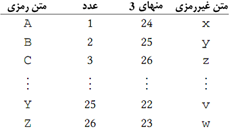
سایفر
سِزار از نظر خودش امن بود. هرچه باشد بیشتر کسانی که ممکن بود به یکی از پیامهای
او دست پیدا کنند حتی خواندن بلد نبودند، چه رسد به اینکه سایفر او را تحلیل کنند.
ولی از نظر رمزنگاری نوین، این روش یک اشکال عمده دارد، و آن این است که وقتی شما
فهمیدید که شخصی از سایفر سزار استفاده میکند، آنگاه همه چیز این سیستم برای شما
روشن است. در اینجا هیچ کلید (key)، یا اطلاعات اضافهای،
وجود ندارد که شما توسط آن بتوانید سایفر خود را تغییر دهید. چنین چیزی، ایده
بسیار بدی بحساب میآید.
برای لحظهای
تامل کنید. سایفر شما یا مخفی است یا نیست، مگر چه اهمیتی دارد که کلید داشته
باشد؟ این نظری بود که در زمان سزار و قرنها پس از او رواج داشت. ولی در سال
1883، آگوست کرکهوفس (Auguste Kerckhoffs) یک مقاله انقلابی را
در این مورد منتشر کرد که در آن میگوید: ”سیستم نباید به مخفیکاری نیاز داشته
باشد و باید طوری باشد که اگر توسط دشمن دزدیده شد، مشکلی را بوجود نیاورد.“ عجب!
چگونه میشود دزدیدن پیام رمزی شما مشکلی را بوجود نیاورد؟
کرکهوفس
در پاسخ به این نکته اشاره میکند که برای شخصی بنام ایو (Eve)،
که دراینجا نقش یک استراقسمع
کننده (Eavesdropper)
را بازی میکند، خیلی آسان خواهد بود که بفهمد آلیس و باب از چه سیستمی استفاده میکنند.
در زمان کرکهوفس برای امور نظامی و دولتی از سیستمهایی استفاده میشد که شبیه
سایفر سِزار بودند، و همین باعث شده بود که کرکهوفس به اطلاعاتی فکر کند که ممکن
بود دشمن از طریق رشوه دادن یا به اسارت گرفتن یکی از افرادِ آلیس یا باب بدست
آورد. چنین نگرانیهایی هنوز هم در دنیای امروز وجود دارند، و چیزهایی مثل استراق
سمع تلفنی، یا نصب نرمافزارهای جاسوسی روی کامپیوترها، را میتوان برای آن ذکر
کرد.
از سوی
دیگر، اگر آلیس و باب سیستمی داشته باشند که برای رمزگذاری و رمزگشایی به یک کلید
نیاز داشته باشد، آنگاه اوضاع زیاد هم بد نخواهد بود. اگر ایو بفهمد که آلیس و باب
از چه سیستمی استفاده میکنند، باز هم نمیتواند بسادگی پیامهای آنها را بخواند.
تلاش برای خواندن یک پیام، آنهم بدون داشتن کلید، یا سعی در یافتن کلید یک پیام، تحلیلرمز
پیام یا تحلیل سایفر نامیده میشود، و بطور کلی به آن شکستن رمز نیز میگویند.
حتی اگر ایو بتواند کلید آلیس و باب را پیدا کند، باز هم امکان جبران خسارت وجود
دارد. اگر آلیس و باب زرنگ باشند، آنها بطور مرتب کلید خودشان را تغییر میدهند.
این کار سختی نیست، زیرا سیستم تغییری نمیکند و همان سیستم قبلی است، و حتی اگر
ایو کلید بعضی از پیامها را پیدا کند، با تغییر کلید او نخواهد توانست همه آنها
را بخواند.
بعنوان یک مثال ساده، ما میتوانیم همین کار را برای
سیستم سِزار انجام دهیم و آن را طوری تغییر دهیم که به کلید خاصی وابسته باشد.
برای شروع، این منطقی است که بپرسیم چرا آلیس حروف غیررمزی خودش را تنها 3
حرف به جلو انتقال میدهد، و نه تعداد دیگری؟ دلیل خاصی برای اینکار وجود ندارد؛
شاید سِزار از عدد 3 خوشش میآمده. جانشین او
آگوستوس، از سیستمی استفاده میکرد که حروف را تنها بهاندازه یک حرف به راست
جابجا میکرد. سایفری بنام rot13 (rot مخفف rotation به معنای چرخش
است) وجود دارد که حروف را به اندازه 13 حرف بجلو جابجا میکند.
در اینترنت معمولاً برای پنهان کردن جُکها و برخی از مطالبی که ممکن است بعضیها آنها را توهینآمیز بدانند از این سایفر
استفاده میشود. سیستمی که در آن حروف به اندازه k حرف جابجا میشود (یا
بعبارتی، جمع k
به پیمانه 26) یک سایفر
انتقالی (shift cipher)
یا سایفر جمعی (additive cipher) با کلید k
نامیده میشود. برای مثال اگر یک
سایفر انتقالی با کلید 21 را درنظر بگیرید،
آنگاه پیام سِزار بصورت زیر خواهد بود:
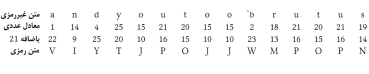
دراینجا
چند کلید میتواند وجود داشته باشد؟ اگر حروف را به اندازه 0 حرف انتقال دهیم، این
اصلاً فکر خوبی نیست، ولی با اینحال شما میتوانید اینکار را انجام دهید. انتقال
به اندازه 26 حرف نیز مثل انتقال به اندازه 0 حرف است (بعبارت دیگر
در حساب به پیمانه 26، 0 و 26
یکی هستند). انتقال به اندازه 27 حرف نیز مثل این است که
حروف را به اندازه 1 حرف جابجا کرده باشید، و به
همین ترتیب. بنابراین 26 انتقال، یا بعبارتی 26
کلید، هستند که به شما نتایج متفاوتی را میدهند. توجه داشته باشید که این شامل 0
نیز میشود، یعنی همان کلید احمقانهای، که کاربرد آن هیچ تغییری در پیام ایجاد
نمیکند. سایفری که هیچ کاری انجام نمیدهد، اصطلاحاً سایفر بیمایه (trivial cipher) نامیده میشود. فرض
کنید آلیس با استفاده از سایفر انتقالی پیامی را برای باب میفرستد و ایو نیز بطور
مخفیانه این پیام رمزگذاری شده را دریافت میکند. حتی اگر ایو به طریقی بفهمد که آلیس
و باب از سایفر انتقالی استفاده میکنند، او هنوز هم برای رمزگشایی پیام باید 26
کلید مختلف را امتحان کند. این خیلی زیاد نیست، ولی هر چه باشد از سایفر سِزار
بهتر است.
آیا میتوانیم تعداد کلیدها را بالاتر ببریم؟ مثلاً
بجای اینکه حروف را به سمت راست انتقال دهیم، آنها را به سمت چپ انتقال دهیم؟
متاسفانه این روش کمک چندانی در بالاتر بردن تعداد کلیدها نمیکند. برای نمونه فرض
کنید ما حرف متنغیررمزی خودمان را 1 حرف به سمت چپ انتقال
دهیم، و هنگامی که به ابتدا رسیدیم، به آخر بازگردیم.

توجه
داشته باشید که بدلیل اینکه 0 معادل 26
به پیمانه 26 است، ما میتوانیم هر دو آنها را بجای هم، و به حرف Z
نسبت دهیم. اگر در اینمورد فکر کنید
خواهید دید که انتقال 1 حرف به سمت چپ، با
انتقال 25 حرف به راست معادل است. یا اگر به زبان حساب پیمانهای
صحبت کنیم، شما میتوانید انتقال به چپ را بعنوان انتقال منفی درنظر بگیرید،
بنابراین در پیمانه 26، -1 با 25
یکی است. پس در اینمورد انتقال به چپ کمکی نمیکند.
بیایید به
نوع دیگری از سایفر توجه کنیم، که سایفرِ حذفِ
ترتیبی (decimation method) نامیده میشود. برای اینکار ما کلیدی مانند 3 را انتخاب میکنیم. و
کار خودمان را با نوشتن حروف الفبای متن غیررمزی شروع میکنیم:
![]()
سپس حروف را سه تا سه تا میشماریم و به هر حرفی که
رسیدیم آن را خط میزنیم (آن را حذف میکنیم) و این حروف را بعنوان حرف رمزی خودمان در پایین مینویسم.

هنگامی که به انتها رسیدید، دوباره به ابتدا
بازگردید. در اینحالت، ”a“
را خط بزنید و کار را ادامه دهید.

نهایتاً به ”b“ بازگردید و کار را تمام کنید:
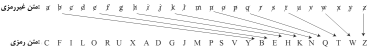
ترجمه نهایی ما از متن غیررمزی به متنرمزی بصورت
زیر خواهد بود:

بسیار خوب، حالا بیایید سعی کنیم مثل یک ریاضیدان به
اینمورد نگاه کنیم. ما چطور میتوانیم روش حذف ترتیبی را به زبان حساب پیمانهای
بیان کنیم؟ خوب، ابتدا باید حروف خود را به اعداد تبدیل کنیم:

خیلی جالب
است! تنها کاری که ما برای گرفتن هشت حرف اول حروف رمزی باید انجام دهیم این است
که اعداد متناظر با حروف غیررمزی را در 3 (کلید) ضرب کنیم. این
روش برای حرف i
جواب نمیدهد زیرا 9 ضرب در 3 میشود 27،
ولی 27 در پیمانه 26 معادل 1 است، که معادل حرف رمزی ما، یعنی A است.
ظاهراً در سایفر فوق، چیز خاصی در مورد عملِ جمع
وجود ندارد. حالا ما بجای جمع کردن هر یک از اعداد متن غیررمزی خودمان با 3،
میتوانیم آنها را در 3 ضرب کنیم، و هنگامی
که به 26 رسیدیم دوباره به ابتدا بازگردیم. از نظر ”حساب ساعتی“
نیز چنین چیزی معقول بنظر میرسد: کار را با نیمه شب شروع کنید. سه برابر ساعت 3
میشود ساعت 9:00. سه برابر ساعت 4 میشود ساعت 12:00.
سه برابر ساعت 5 میشود ساعت 15:00
(یا به عبارتی همان ساعت 3 بعد از ظهر) و به
همین ترتیب. حالا ما یک سایفر ضربی (multiplicative cipher)
داریم که بصورت زیر خواهد بود:
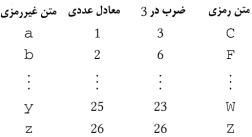
اگر بخواهیم پیام ”be fruitful and multiply“ را با استفاده از
این روش رمزگذاری کنیم، شبیه زیر خواهد بود:

ضمناً
برای حل مسئله بازگشت به ابتدا، بجای اینکه بارها و بارها عدد مورد نظر را از 26
کم کنیم، بهتر است روش سریعتری داشته باشیم. خوشبختانه برای اینکار راهحلی وجود
دارد که شما از دوران دبستان با آن آشنا هستید، و آن انجام عمل تقسیم و بدست آوردن
باقیمانده است. در اینجا تنها کاری که باید انجام دهیم این است که ببینیم در عدد
مورد نظر ما چند 26
وجود دارد، سپس آنها را کنار گذاشته و
فقط باقیمانده را نگاه داریم. برای مثال، برای رمزگذاری آخرین حرفِ مثالِ قبل، من 25
را در 3 ضرب کردم، که حاصل آن میشود 75. سپس 75
را به 26 تقسیم کردم، که خارج قسمت آن شد 2،
من آن را کنار گذاشتم و باقیمانده این تقسیم که 23 میشود را نگاه
داشتم. این باقیمانده همان عددی است که من برای متنرمزی خودم به آن نیاز دارم.
روش دیگری که میتوان این را در نظر گرفت این است که بگوییم 75=2×26+23؛
این یعنی 75 دوبرابر 26 است با باقیمانده 23.
ولی 26 به پیمانه 26 برابر 0
است، پس میتوانیم بگوییم در پیمانه 26، عدد 75
برابر است با 2×0+23=23.
سایفر
ضربی چند کلید دارد؟ در نگاه اول ممکن است انتظار داشته باشید که دوباره این تعداد
26 باشد، که شامل آن کلید مسخره، یعنی 0 هم بشود. ولی صبر کنید، در پیمانه 26، ضرب یک عدد در 26
مثل ضرب آن در 0 است. و ضرب
در 0 بد است. نه فقط مسخره، بلکه بد است. یک سایفر ضربی که کلید
آن 0 باشد مانند زیر است:
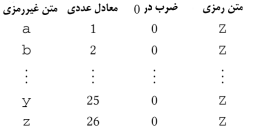
بنابراین اگر با این سایفر پیامی را رمزگذاری کنیم،
بصورت زیر در میآید:
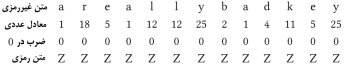
هیچ روشی
در دنیا یافت نمیشود که بتوان پیام فوق را رمزگشایی کرد! بنابراین ما نمیتوانیم
از 0 بعنوان یک کلید استفاده کنیم.
آیا کلیدهای دیگری نیز هستند که ما نتوانیم از آنها
استفاده کنیم؟ ضرب در 2 را درنظر بگیرید. ما
میدانیم هر عددی که در 2 ضرب شود، حاصل آن یک
عدد زوج خواهد بود. یک سایفر ضربی که کلید آن 2 باشد مثل زیر است:
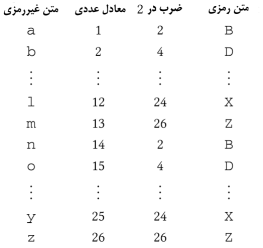
هر چند
اینمورد بهتر از ضرب در 0 است، ولی هنوز هم
وقتی میخواهیم آن را رمزگشایی کنیم، مشکل ساز است: مثلاً متنرمزی B میتواند هم معادل متن
غیررمزی a باشد و هم معادل متن
غیررمزی n. مشابه با این، برای
هر حرف رمزی دو حرف غیررمزی وجود دارند، که این باعث میشود 13 کلید (کلیدهای زوج)
نامناسب باشند، و بنابراین 13 کلید باقی میماند.
البته یک کلید بد دیگر هم وجود دارد، سعی کنید خودتان آن را پیدا کنید. بنابراین
برای سایفر ضربی 12 کلید مناسب باقی میماند، از
جمله ضرب در 1، که برای سایفر ضربی یک کلید بیمایه محسوب میشود.
ما درمورد
رمزگذاری یک پیام با استفاده از سایفر ضربی صحبت کردیم ولی چیزی از رمزگشایی آن
نگفتیم. بخاطر دارید که برای رمزگشایی یک پیام باید عکس آن کاری را انجام دهید که
برای رمزگذاری آن انجام دادید. برای رمزگشایی یک سایفر سِزار شما بجای انتقال به
راست، حرف مورد نظر را 3 حرف به سمت چپ انتقال
میدادید. برای رمزگشایی یک سایفر انتقالی، که کلید آن k باشد، شما k حرف به سمت چپ میروید.
درمورد سایفر ضربی چطور؟ خوب شما میتوانید برای همه حروف یک جدول بزرگ تشکیل دهید
و از آن برای رمزگشایی حروف استفاده کنید. ولی ممکن است برای پیامهای خیلی کوتاه
نخواهید یک جدول کامل تشکیل دهید. در اینجا باید پرسید چطور میشود عمل ضرب را
معکوس کرد؟
معلوم
است، همه میدانند که عکس عمل ضرب تقسیم است. معکوس ضرب در 3، تقسیم بر 3
است. در سایفر ضربی ما، که کلید آن 3 است، این روش برای
برخی از حروف بخوبی جواب میدهد. حرف رمزی C که معادل عددی آن 3 است، با تقسیم بر 3
به 1 تبدیل میشود، که معادل حرف غیررمزی a است. حرف رمزی F که معادل عددی آن 6
است، با تقسیم بر 3 به 2 تبدیل میشود، که
معادل حرف غیررمزی b
است. ولی درمورد A
چطور؟ معادل عددی آن 1 است که با تقسیم بر 3
حاصل آن ![]() میشود،
که معادل هیچ حرفی نیست. راه حل این مسئله بازگشت به ابتدا است. عدد 1
معادل 27 به پیمانه 26 است، بنابراین
ما میتوانیم بگوییم A
همان 27 است، که بر 3 قابل قسمت است و حاصل
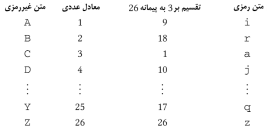
آن 9 میباشد، که معادل حرف i است. به همین ترتیب در پیمانه 26،
B نه فقط میتواند 2
باشد، بلکه میتواند 28 و 54 نیز باشد، و 54
تقسیم بر 3 برابر است با 18، بنابراین B با r متناظر است.
میشود،
که معادل هیچ حرفی نیست. راه حل این مسئله بازگشت به ابتدا است. عدد 1
معادل 27 به پیمانه 26 است، بنابراین
ما میتوانیم بگوییم A
همان 27 است، که بر 3 قابل قسمت است و حاصل
آن 9 میباشد، که معادل حرف i است. به همین ترتیب در پیمانه 26،
B نه فقط میتواند 2
باشد، بلکه میتواند 28 و 54 نیز باشد، و 54
تقسیم بر 3 برابر است با 18، بنابراین B با r متناظر است.

این روش
سعی و خطا جواب میدهد، ولی کارآیی آن بیشتر از تشکیل یک جدول نیست. برای مثال،
فرض کنید کلید شما بجای 3، 15
باشد. در اینحالت، حرف رمزی B معادل چه حرف غیررمزی خواهد بود؟ در پیمانه 26، این میتواند با هر
یک از اعداد 2، 28، 54،
80، 106، 132،
... معادل باشد.
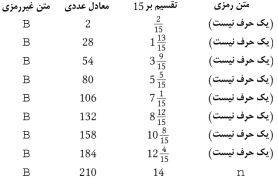
شما برای
پیدا کردن عددی که بر 15 قابل تقسیم باشد
مجبورید 9 عدد را امتحان کنید، و هیچ تضمینی وجود ندارد که برای
حروف دیگر وضعیت بدتر از این نباشد. چیزی که حقیقتاً مفید خواهد بود، یک عدد صحیح
است که به پیمانه 26 جواب دهد، درست مثل ![]() که برای
اعداد معمولی جواب میدهد. ما این عدد را
که برای
اعداد معمولی جواب میدهد. ما این عدد را ![]() مینامیم.
آنگاه ضرب در
مینامیم.
آنگاه ضرب در ![]() به
پیمانه 26، برابر ضرب در
به
پیمانه 26، برابر ضرب در ![]() به
پیمانه 26 خواهد بود، که مثل
این است که یک عدد را در پیمانه 26
بر 3 تقسیم میکنیم.
به
پیمانه 26 خواهد بود، که مثل
این است که یک عدد را در پیمانه 26
بر 3 تقسیم میکنیم.
چرا ممکن
است ما فکر کنیم ![]() وجود
دارد؟ اگر به سایفر ضربی خودمان که کلید 3
داشت نگاه مجددی بیاندازیم، مانند زیر خواهد بود:
وجود
دارد؟ اگر به سایفر ضربی خودمان که کلید 3
داشت نگاه مجددی بیاندازیم، مانند زیر خواهد بود:
بنظر میرسد
که شاید تقسیم بر 3 به پیمانه 26، معادل است با ضرب در 9
به پیمانه 26. اگر این درست باشد،
آنگاه برای رمزگشایی حرفی مثل E، باید محاسبه زیر را انجام
دهیم:

هنگامی که
ما فهمیدم ![]() چیست،
بعد از آن بدون اینکه به سعی و خطا، یا جستجو در جدول، نیازی داشته باشیم میتوانیم
این را محاسبه کنیم.
چیست،
بعد از آن بدون اینکه به سعی و خطا، یا جستجو در جدول، نیازی داشته باشیم میتوانیم
این را محاسبه کنیم.
اگر کلید
یک سایفر ضربی برابر k باشد، آیا
میتوانیم مطمئن باشیم که ![]() وجود
دارد؟ اگر وجود داشته باشد، چگونه آن را پیدا کنیم؟ پاسخ به این سئوالات ما را کمی
منحرف میکند، و ما را به ”کلیدهای بدِ“ سایفر ضربی که قبلاً در مورد آنها صحبت
کردیم میکشاند.
وجود
دارد؟ اگر وجود داشته باشد، چگونه آن را پیدا کنیم؟ پاسخ به این سئوالات ما را کمی
منحرف میکند، و ما را به ”کلیدهای بدِ“ سایفر ضربی که قبلاً در مورد آنها صحبت
کردیم میکشاند.
ما
فهمیدیم که یک سایفر ضربی کلیدهای بدی مثل 2,
4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, دارد، علاوه
بر اینها، کلید بد دیگری نیز هست که قرار بود خودتان بعنوان تمرین آن را پیدا
کنید، و آن 13 است. چیزی که این
اعداد در آن مشترک هستند این است که همه آنها یا مضربی از 2
یا 13، و یا هر دو آنها
هستد. توجه کنید که 2×13=26، و اینمورد اتفاقی
نیست. اگر ما از الفبای قدیم رومی که 21
حرف داشت استفاده کنیم (یعنی پیمانه ما 21
باشد)، بدلیل اینکه 21=3×7، آنگاه کلیدهای بَد
ما مضربهایی از 3 یا 7 (یا هر دو) خواهد بود. زبان رومانیایی دارای 28 حرف است، و 28=2×2×7،
پس کلیدهای بد ما مضربهایی از 2
یا 7 (یا هر دو) خواهند
بود. در زبانهای دانمارکی، نروژی، و سوئدی 29
حرف وجود دارد، بنابراین چون 29
اول است، تنها کلید بد، خود این عدد (یعنی 29)
میباشد.
کاری که ما با این تعداد حروف کردیم (26, 21, 28, 29) شکستن آنها به عواملی است که
ساده شدنی نیستند، و اعداد اول (prime numbers)
نامیده میشوند. این کار تجزیه (factoring)
نام دارد، و تنها به یک طریق میتواند انجام شود. این حقیقت از زمانهای بسیار دور
شناخته شده بود و قدمت آن به قرن چهارم قبل از میلاد باز میگردد، یعنی زمانی که اقلیدس (Euclid) آن را در کتاب اصول (Elements)
خود مطرح کرد. آنچه ما میخواهیم بدانیم این است که آیا کلید و پیمانه ما دارای مقسومعلیه مشترکی (common divisor)
هستند یا نه، یعنی آیا عددی هست که بتواند هر دو آنها را تقسیم کند. عدد 1 همیشه دو عدد ما را تقسیم میکند، ولی این عدد بیمایه
است و برای اینکار بحساب نمیآید. در کتاب اصول اقلیدس روشی آمده که به ما نشان میدهد
چگونه با یافتن بزرگترین
مقسومعلیه مشترک،
یا بمم (GCD)،
میتوانیم مقسومعلیه مشترک دو عدد را پیدا کنیم. روشی که توسط آن میتوانیم بمم
دو عدد را پیدا کنیم، الگوریتم
اقلیدسی (Euclidean
algorithm) نامیده میشود، هرچند ما حقیقتاً نمیدانیم که آیا این
خود اقلیدس بوده که این روش را اختراع کرده یا آن را از کس دیگری قرض گرفته.
الگوریتم یعنی روش انجام دادن کاری که بخوبی تعریف شده باشد و درست شبیه یک برنامه کامپیوتر، همیشه برای
هر ورودی که به آن داده میشود، یک جواب مشخص و صحیح را تولید کند. در زیر نمونهای
از الگوریتم اقلیدسی را میبینید که از آن برای پیدا کردن بمم 756 و 210
استفاده شده.
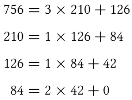
درست
مانند آنچه قبلاً انجام دادیم، در اینجا نیز هر مرحله شامل تقسیم یک عدد صحیح و
بدست آوردن خارج قسمت و باقیمانده آن است. نتیجه نهایی بزرگترین مقسومعلیه مشترک
(بمم) 756
و 210 میباشد. این عدد آخرین
باقیمانده غیرصفر تقسیم، یعنی 42،
است.
ما میتوانیم از این الگوریتم استفاده کنیم و ببینیم
آیا 6 جزء کلیدهای بد است
یا نه. ما اینکار را با محاسبه بمم 6
و 26 انجام میدهیم:
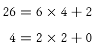
بدلیل اینکه 2
هم 6 و هم 26 را تقسیم میکند، درنتیجه
ما میبینیم که6 یک کلید بد
است. اگر یک کلید خوب، مثل 3،
داشته باشیم، در این صورت این روش چه نتیجهای خواهد داشت؟
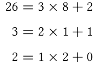
بزرگترین
عددی که هم 3 و هم 26 را تقسیم کند 1 است، که بحساب نمیآید. بنابراین 3
کلید خوبی است.
ممکن است
شما تعجب کنید که چرا ما بجای اینکه دو عدد را به عوامل اول تجزیه کنیم و به عوامل
مشترک آنها نگاه کنیم، چرا
به خودمان زحمت میدهیم و از الگوریتم اقلیدسی برای اینکار استفاده میکنیم. دو
پاسخ برای این سؤال وجود دارد: اول اینکه ما نهایتاً متوجه خواهیم شد که این
الگوریتم برای اعداد بزرگ سریعتر از تجزیه آنها جواب میدهد. و دوم اینکه وقتی ما
الگوریتم اقلیدسی را انجام دادیم میتوانیم با ترفندی مشابه، ![]() را بدست
آوریم.
را بدست
آوریم.
هدف بعدی ما این است که دو چیز را بدست آوریم: یکی ”3 ضرب در چیزی“ و دیگری ”26
ضرب در چیزی“. ما معادلات الگوریتم اقلیدسی مربوط به 3
و 26 را در سمت چپ مینویسیم، و هر
بار که در سمت راست قسمتی را ببینیم که در آن 3
یا 26 نباشد، ما از خط قبلی
برای جایگرین کردن آن با 3ها و 26ها استفاده میکنیم.

حالا ما 1 را بصورت یک قسمت 3تایی و یک قسمت 26 تایی نوشتهایم. چرا اینکار را میکنیم؟ خوب بخاطر اینکه ما میخواهیم در
پیمانه 26 کار کنیم، و در
پیمانه 26، خود 26 با 0
برابر است، بنابراین
1=
(3 × 9) –(26 × 1)
که یعنی،
1
≡ (3 × 9) –(26 × 1) (26 به پیمانه)
یا
1
≡ (3 × 9) (26 به پیمانه)
یا
![]() ≡ 9 (26 به پیمانه)
≡ 9 (26 به پیمانه)
پس حالا ما توانستیم تایید کنیم که 9 همان ![]() است، که
مانند
است، که
مانند ![]() در
پیمانه 26 عمل میکند. بار دیگر
ممکن است بنظر برسد که ما با استفاده از روش سعی و خطا میتوانستیم همین نتیجه را
سریعتر بدست آوریم. ممکن است برای اعداد کوچک اینطور باشد، ولی روش فوق برای اعداد
بزرگ خیلی سریعتر جواب میدهد.
در
پیمانه 26 عمل میکند. بار دیگر
ممکن است بنظر برسد که ما با استفاده از روش سعی و خطا میتوانستیم همین نتیجه را
سریعتر بدست آوریم. ممکن است برای اعداد کوچک اینطور باشد، ولی روش فوق برای اعداد
بزرگ خیلی سریعتر جواب میدهد.

ضمناً یک
اصطلاح فنی برای ![]() هست،که ”وارون ضربی 3
به پیمانه 26“ نام دارد. در بسیاری
از حوزههای ریاضیات ایده کلی معکوس یا وارون (inverses)
اهمیت زیادی دارد. تا اینجای کار، ما وارونِ
جمعی (که همان
تفریق باشد)، و وارونِ ضربی را دیدهایم، و بعداً در ادامه این کتاب با نمونههای
دیگری از وارون نیز آشنا خواهیم شد. در حساب پیمانهای نکته خوبی در مورد وارونها
وجود دارد که باید به آن اشاره کرد، و آن این است که معمولاً میان یک عدد و وارون
آن یک تفاوت کمیتی وجود ندارد. این یعنی در حساب عادی، وارون عدد مثبت 2 ، عدد منفی -2
است. ولی ما در حساب به پیمانه 26
داریم −2≡24. بنابراین، در حساب
به پیمانه 26، 2 و 24
وارون یکدیگرند ولی توجه کنید که هیچکدام ”منفی“ نیستند. به همین نحو، در حساب
عادی 3 یک عدد صحیح، و وارون
آن
هست،که ”وارون ضربی 3
به پیمانه 26“ نام دارد. در بسیاری
از حوزههای ریاضیات ایده کلی معکوس یا وارون (inverses)
اهمیت زیادی دارد. تا اینجای کار، ما وارونِ
جمعی (که همان
تفریق باشد)، و وارونِ ضربی را دیدهایم، و بعداً در ادامه این کتاب با نمونههای
دیگری از وارون نیز آشنا خواهیم شد. در حساب پیمانهای نکته خوبی در مورد وارونها
وجود دارد که باید به آن اشاره کرد، و آن این است که معمولاً میان یک عدد و وارون
آن یک تفاوت کمیتی وجود ندارد. این یعنی در حساب عادی، وارون عدد مثبت 2 ، عدد منفی -2
است. ولی ما در حساب به پیمانه 26
داریم −2≡24. بنابراین، در حساب
به پیمانه 26، 2 و 24
وارون یکدیگرند ولی توجه کنید که هیچکدام ”منفی“ نیستند. به همین نحو، در حساب
عادی 3 یک عدد صحیح، و وارون
آن ![]() یک عدد
کسری است، ولی با وجود اینکه هیچ یک از اعداد 3
و 9 ”کسری“ نیستند، آنها به
پیمانه 26 وارون ضربی یکدیگر
هستند. این ویژگی به مواردی اختصاص دارد که تنها تعداد متناهی از اعداد وجود دارند
که متمایز حساب میشوند. راه دیگری که میشود به این مسئله نگاه کرد این است که در
این موارد یک تمایز واقعی میان جلو و عقب وجود ندارد. به همین ترتیب، برای سایفری
که از این عملیات استفاده میکند هیچ تفاوت ریاضی میان رمزگذاری و رمزگشایی وجود
ندارد (هنگامی که وارون را بدست آوردید، شما برای بازگشت به عقب میتوانید به جلو
بروید). این مطلب برای مطالعه بخشهای بعدی مهم است، و پیش از اینکه آنها را
مطالعه کنید، ممکن است بخواهید بیشتر در مورد آن فکر کنید.
یک عدد
کسری است، ولی با وجود اینکه هیچ یک از اعداد 3
و 9 ”کسری“ نیستند، آنها به
پیمانه 26 وارون ضربی یکدیگر
هستند. این ویژگی به مواردی اختصاص دارد که تنها تعداد متناهی از اعداد وجود دارند
که متمایز حساب میشوند. راه دیگری که میشود به این مسئله نگاه کرد این است که در
این موارد یک تمایز واقعی میان جلو و عقب وجود ندارد. به همین ترتیب، برای سایفری
که از این عملیات استفاده میکند هیچ تفاوت ریاضی میان رمزگذاری و رمزگشایی وجود
ندارد (هنگامی که وارون را بدست آوردید، شما برای بازگشت به عقب میتوانید به جلو
بروید). این مطلب برای مطالعه بخشهای بعدی مهم است، و پیش از اینکه آنها را
مطالعه کنید، ممکن است بخواهید بیشتر در مورد آن فکر کنید.
تا اینجا
ما یک سایفر انتقالی با 26
کلید خوب داریم، که در میان آنها استفاده از کلید 1
مسخره است، و همچنین یک سایفر ضربی با 12
کلید خوب داریم، که باز هم در میان آنها استفاده از کلید 1
مسخره است. برای ایو (یا همان استراقسمع کننده ما) خیلی ساده خواهد بود تا با
استفاده از حملات فراگیر (brute-force attack)
هر دو این رمزها را بشکند. حملات فراگیر به روشهایی گفته میشود که در آن شخص
حمله کننده کلیه کلیدهای ممکن را امتحان میکند تا بالاخره به کلید صحیح دست پیدا
کند. اگر آلیس و باب یکی از این سایفرها را برای خودشان انتخاب کنند، هنوز هم برای
ایو 38 انتخاب میماند که
آنها را امتحان کند. ولی اگر آلیس و باب بتوانند بیشتر از یک سایفر را بکار
بگیرند، آنوقت وضعیت به چه صورت درمیآید؟
بدلیل
اینکه توضیح غیر-ریاضی چنین مواردی میتواند بالقوه پیچیده شود، در اینجا ما نیاز
داریم تا مفاهیم ریاضی بیشتری را
معرفی کنیم. ما P را بعنوان
عددی درنظر میگیریم که میان 1
تا 26 است، و نشان دهنده یک
حرف غیررمزی میباشد. و C را بعنوان عددی که نشاندهنده
یک حرف رمزی است در نظر میگیریم. در اینجا نیز k نشان دهنده کلید است.
دراینصورت رمزگذاری با استفاده از یک سایفر انتقالی با کلید k،
میتواند بصورت زیر نوشته شود:
C ≡ P + k (26 به
پیمانه)
و
رمزگذاری با استفاده از یک سایفر ضربی با کلید k نیز میتواند
بصورت زیر نوشته شود:
C ≡ kP (26 به
پیمانه)
بطور
مشابه، رمزگشایی در سایفر انتقالی بصورت زیر است:
P ≡ C - k (26 به
پیمانه)
و رمزگشایی
با استفاده از یک سایفر ضربی با کلید k نیز میتواند بصورت زیر نوشته
شود:
C ≡ ![]() P
(26 به پیمانه)
P
(26 به پیمانه)
اگر آلیس
سعی کند برای رمزگذاری از دو کلیدِ انتقالِ مختلف، مثل k و m،
استفاده کند، وضعیت چگونه میشود؟ آیا چنین کاری موجب میشود تا رمزگذاری دو برابر
امنتر شود؟ اینمورد شبیه زیر است:
C ≡ P + k + m (26 به
پیمانه)
متاسفانه
چنین چیزی از نظر ایو همان تاثیری را دارد که آلیس و باب بخواهند از کلید k+m
استفاده کنند، بنابراین ایو مانند قبل میتواند با استفاده از حمله فراگیر رمز را
بشکند. همین حالت برای موقعی که آلیس و باب از سایفر ضربی با کلیدهای متفاوت
استفاده کنند نیز صادق است. ولی اگر از ترکیبی از این دو روش استفاده شود چطور؟
مثلاً فرض کنید آلیس ابتدا حرف غیررمزی را در k ضرب کند و سپس m[1]
را به آن اضافه کند:
C ≡ kP +
m (26 به پیمانه)
و باب نیز
ابتدا m
را از کم کند و سپس حاصل را در ![]() ضرب کند:
ضرب کند:
P ≡ ![]() (C − m) (26 به پیمانه)
(C − m) (26 به پیمانه)
توجه کنید
که باب نه فقط عملیات را معکوس کرده، بلکه ترتیب آنها را نیز معکوس کرده است! اگر
چنین چیزی زیاد مفهوم نیست، برای روشنتر شدن آن، عملیات کفش به پا کردن و کفش از
پا درآوردن را در نظر بگیرید. شما برای کفش به پاکردن ابتدا باید جورابهایتان را
به پا کنید، و سپس کفشهای خود را بپوشید. برای جوراب از پا در آوردن شما مجبور
هستید هر دو آنها را در آورید، ولی به ترتیب معکوس.
این ترکیب
نوع جدیدی از سایفر را در اختیار ما قرار میدهد، که به زبان فنی یک سایفر مستوی یا سایفر
آفین (affine
cipher) نامیده میشود، هرچند من برخی اوقات ترجیح میدهم آن را
سایفر kP
+ m بنامم. در اینحالت برای m 12
انتخاب، و برای m 26 انتخاب وجود دارد،
بنابراین 12×26=312 کلید مختلف برای
این سایفر وجود دارد. همین کافی است که استفاده از روش حمله فراگیر برای ایو کمی
مشکلتر شود، هرچند اگر او به کامپیوتر دسترسی داشته باشد، باز هم چنین چیزی سخت
نخواهد بود.
ایده ترکیب دو سایفر باهم و ساختن یک سایفر ترکیبی (product cipher)
سابقه تاریخی طولانی دارد و به سالها قبل باز میگردد. جالب است اشاره کنم که
سایفر قدیمیتری هست که آن نیز بصورت kP + m است. نام این سایفر آتبَش (atbash) است، و قدمت آن حداقل به یکی
از کتابهای مقدس یهودیان، یعنی کتاب ارمیای نبی (Jeremiah)
باز میگردد. مانند روش حذف ترتیبی، این سایفر نیز کار خود را با نوشتن حروف
الفبای غیررمزی شروع میکند، که در زیر آن حروف الفبای رمزی بترتیب عکس نوشته شدهاند.
در اینجا ما بجای حروف عبری از حروف زبان انگلیسی استفاده میکنیم:

خوب پس چرا ما این سایفر را نوعی از سایفر kP + m
محسوب میکنیم؟ زیرا وقتی ما حروف را به اعداد تبدیل میکنیم، خواهیم داشت:

ما خواهیم
دید که متنرمزی از قاعده زیر پیروی میکند:
C ≡27 - P (26 به پیمانه)
البته میتوانیم
آن را بصورت زیر بنویسیم:
C ≡ (-1)P + 27
(26 به پیمانه)
که در
پیمانه 26 برابر است با:
C ≡ 25P + 1 (26 به پیمانه)
بنابراین
این سایفر، همان سایفر kP + m است که کلیدهای آن k=25 و m=1 هستند.
اگر ما به
این مسیری که برای پیچیدهتر کردن عملیات خودمان به پیمانه 26
اتخاذ کردیم ادامه دهیم، نهایتاً به راهی دست پیدا خواهیم کرد که هر یک از حرف
غیررمزی را به حرف دیگری تبدیل کنیم. بنابراین حرف a میتواند در متنرمزی
با هر یک از 26 جایگزین شود.
پس از آن ما میتوانیم b را با هر یک از 25 حرف باقیمانده جایگزین کنیم. ما هنوز هم 24 حرف جایگزین نشده برای حرف c داریم، و 23 تا برای d و ... به همین ترتیب، تا
اینکه نهایتاً فقط یک حرف برای جایگزینی z باقی میماند. چنین سایفری،
یک سایفر جایگزینی تکنگاری تکالفبایی نامیده میشود. در اینجا تکنگاری (monographic)
به معنای این است که این سایفر هر بار یک حرف را جایگزین میکند، و تکالفبایی (monoalphabetic)
نیز به این معنی است قواعد جایگزینی برای تمام حروفِ پیام یکی است. نام این سایفر
نسبتاً طولانی است، و یک سایفر معمولی محسوب میشود، بنابراین برای صرفهجویی در
وقت ما آن را سایفر جایگزینی ساده مینامیم. برای ساختن چنین سایفری، روی هم
رفته 26×25×24×···×3×2×1 راه مختلف وجود دارد، که برابر است با 403,291,461,126,605,635,584,000,000 . علاوه بر آن سه سایفری که قبلاً آنها را
توضیح دادیم، این سایفر برخی پیامهای رمزی را نیز در بردارد که در بسیاری از
روزنامهها چاپ میشوند. اگر ایو بخواهد چنین پیامهایی را با روش حمله فراگیر
بشکند، باید کلیدهای زیادی را امتحان کند. ولی به غیر از حملات فراگیر، روشهای
بهتری برای ایو وجود دارد که با استفاده از آنها میتواند به چنین سایفرهایی حمله
کند.
راه موثری
برای شکستن سایفرهای جایگزینی ساده وجود دارد که تحلیل
تکرار حروف (letter
frequency analysis) نام دارد. قدمت این روش
حداقل به زمان دانشمند عرب زبان، أبو
يوسف يعقوب بن إسحاق الصبّاح الكندي در قرن نهم میلادی باز میگردد. اگر بخواهیم ساده
بگوییم، ایده این روش این است که در بعضی از زبانها، مثل انگلیسی، عربی، و بسیاری
دیگر از زبانهای انسانی، برخی از حروف الفبا هستند که از بقیه کاربرد بیشتری
دارند. برای مثال، در یک متن عادی انگلیسی، حدود %13 از متن را حرف e تشکیل میدهد، یعنی بیش از هر حرف دیگری.
اگر ایو قسمتی از متنرمزی را در دست داشته باشد، که مثلاً در آن حرف R حدود %13 متن را تشکیل دهد، یعنی بیش از حرف دیگری، شانس زیادی
وجود دارد که R (C=18) نشان دهندهe (P=5) باشد. اگر سایفر از نوع جمعی باشد، آنگاه ایو میداند که رابطه زیر برقرار
است
5
+ k ≡ 18 (26 به پیمانه)
بنابراین
شانس زیادی وجود دارد که کلید k=13 باشد.
اگر
سایفری که ایو در دست دارد از نوع دیگری، مثل آفین، باشد آنگاه چنین اطلاعاتی کافی
نخواهد بود. در این صورت ممکن است او بخواهد حرف دیگری، مثل t را حدس بزند، که در
حدود %8 از متون انگلیسی را
تشکیل میدهد، یا حرف a که در %7
موارد تکرار میشود. حالا مثلاً اگر ایو حدس بزند که R نشاندهنده e و F نشاندهنده a است، آنگاه او میداند
که
5k
+ m ≡ 18 (26 به پیمانه),
1k + m ≡
6 (26 به پیمانه).
حالا ایو
دو معادله و دو مجهول را در دست دارد، با کم کردن این دو معادله از یکدیگر ما
خواهیم داشت:
4k ≡ 12 (26 به پیمانه)
همانطور
که قبلاً دیدید، اگر عدد 4
در پیمانه 26 دارای یک وارون بود، آنگاه
ایو میتوانست دو طرف معادله را در آن ضرب کند تا 4
حذف شود و مقدار k را بدست آید. ولی متاسفانه بمم 4
و 26 عدد 2
است، بنابراین 4 در پیمانه 26 وارون ندارد. این یعنی معادلات ما یا جوابی ندارند، یا
بیش از یک جواب دارند. اگر معادلات دارای جوابی نباشند، این یعنی احتمالاً حدس ایو
در مورد تکرار حروف اشتباه بوده و او باید دوباره تلاش کند. ولی معلوم شده که در
اینمورد معادلات بالا دو جواب دارند: k = 3 و k = 16 که در هر دو حالت مقدار m
در پیمانه 26 باید با 6 − 1k برابر باشد. بنابراین جوابهای ممکن
عبارتند از: k = 3 و m = 3 یا k = 16 و m = 16. پس از آن ایو میتواند تلاش
کند تا پیام مورد نظر را با هر یک از جفت کلیدها رمزگشایی کند تا ببیند آیا متنی
که حاصل میشود معنی دار است یا نه. بدلیل اینکه a، t، و چند حرف دیگر
تقریباً به یک اندازه در متون تکرار میشوند، احتمال دارد که هیچ یک از حدسها
صحیح نباشد، که در اینصورت ایو باید کار را از نو شروع کند و ببیند که مقادیر e و a چه میتوانند باشند.
ممکن است اینکار چند بار طول بکشد، ولی در آخر ایو باید بتواند کلید صحیح را پیدا کند
و اینکار نسبت به موقعی که از حمله فراگیر استفاده کند، خیلی سریعتر انجام میشود.
عیب عمده
این روش این است که شما به یک متنرمزی نیاز دارید که طول آن به اندازه کافی بزرگ
باشد. تعدادی که من برای تکرار حروف ذکر کردم فقط مقادیر متوسط بود، و احتمال
زیادی هست که تعداد حروف تکراری در پیامهای کوتاه متفاوت باشند. مثلاً فرض کنید
بخواهید پیام ” Zola is taking zebras to the zoo“
را رمزگذاری کنید.
همانطور که میبینید در این پیام حرف e تنها یکبار تکرار میشود، و
در مقابل حرف z، که بطور متوسط در متون عادی انگلیسی کمترین تکرار را دارد، در
اینجا سه بار تکرار شده است. هنگامی که ما در بخشهای بعدی سایفرهای جایگزینی
پیچیدهتر را تحلیل کنیم، خواهیم دید که چگونه چنین مسئلهای میتواند اوضاع را
پیچیدهتر کند.
روشهای
زیادی وجود دارد که بتوان سایفرهایی را ساخت که در آنها روش تحلیلِ تکرارِ حروف
جواب ندهد، مثلاً شما میتوانید قواعد جایگزینی را طوری تغییر دهید که در جاهای
مختلفِ پیام، بطور متفاوت عمل کند، که به این روش چندالفبایی (polyalphabetic)
میگویند، یا میتوانید قاعده جایگزینی را طوری تعریف کنید که در هر بار جایگزینی
بر روی بیش از یک حرف انجام شود، که به آن چندنگاری (polygraphic)
میگویند. این دو روش در رمزنگاری نوین جایگاه خود را دارند، ولی ما فعلاً به روش
چندنگاری میپردازیم.
اولین
چیزی که در یک سایفر چندنگاری باید درنظر داشته باشید اندازه بلوک (block)
یا قطعه است. سایفرهایی که اندازه بلوک آنها 2
است، دونگاری (digraphic)،
و آنهایی که اندازه بلوک آنها 3
است سهنگاری (trigraphic)
... و غیره نام دارند. قدمت سایفرهای دونگاری به قرن شانزدهم میلادی باز میگردد،
هرچند اولین استفادههای عملی از آنها در قرن نوزدهم بعمل آمد. در سال 1929 یک
ریاضیدان آمریکایی بنام ِلستر هیل (Lester S. Hill) سایفر هیل (Hill
cipher) را اختراع کرد،
که بلوک آن میتواند هر اندازهای را داشته باشد. ما برای مثال خودمان اندازه بلوک این
سایفر را 2 فرض میکنیم. متن غیررمزی خودتان را
به قطعات 2-حرفی تقسیم کنید. اگر بلوک آخر با دو
حرف پر نشده، جای خالی را با حروف تصادفی پر کنید. این حرف، حرف پوچ (null) یا حرف لایهگذاری (padding)
نامیده میشوند.
ja ck ya nd
ji ll ya nd ev ex
بیایید
اولین حرف هر بلوک از متن غیررمزی را P1، و دومین حرف را P2 بنامیم پس از آن دو حرف رمزی را با استفاده از فرمول زیر حساب کنید.
C1
≡ k1P1 + k2P2
(26 به پیمانه)
C2
≡ k3P1 + k4P2
(26 به پیمانه)
که در آن k1،
k2،
k3،
و k4،
اعدادی بین 1 تا 26 هستند، که روی هم رفته کلید سایفر را
تشکیل میدهند. برای مثال اگر کلید 3،
5، 6،
1 باشد، آنگاه فرمولهای بالا
به صورت زیر در میآیند:
C1 ≡ 3P1 +5P2 (26 به پیمانه)
C2
≡ 6P1 + 1P2 (26
به پیمانه)
اگر متن غیررمزی ما بصورت زیر باشد
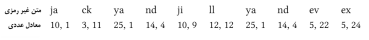
آنگاه
اعداد رمزی دو حرف اول متنرمزی بصورت زیر محاسبه میشود
C1
≡ 3×10 + 5×1≡9 (26
به پیمانه)
C2
≡ 6×10 + 1×1 ≡9 (26 به
پیمانه)
آن x که در پایان متن غیررمزی
وجود دارد پوچ است.
بقیه پیام نیز بطور مشابهی رمزگذاری میشود:
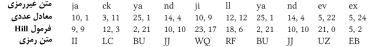
توجه
داشته باشید که آن j که مربوط به لغت jacky است به I، و آن j که مربوط به لغت jily است به W تبدیل شدهاند. به همین
شکل، آن دو l که در لغت
jill وجود دارند نیز هرکدام به حروف مختلفی تبدیل شدهاند، ولی هم j و هم a که در لغت jacky
هستند، هر دو به I تبدیل شدهاند. البته دلیل آن هم این است که حروف بطور جداگانه
رمزگذاری نمیشوند، بلکه اینکار بصورت گروهی انجام میشود. همچنین توجه کنید هر دو
باری که yand در متن غیررمزی آمده، در متنرمزی به BUJJ تبدیل شده.
باب برای
رمزگشایی پیام باید دو معادله زیر را که شامل دو مجهول است حل کند:
C1
≡ k1P1 + k2P2
(26 به پیمانه)
C2
≡ k3P1 + k4P2
(26 به پیمانه)
راههای
زیادی برای حل کردن این
معادلات وجود دارد؛ یکی از آنها این است که معادله بالایی را در k4،
و معادله پایینی را در k2، ضرب کرد و سپس این دو معادله
را از هم کم کرد. برای نمونه، اگر بخواهیم آخرین بلوک مثال قبلی را رمزگشایی کنیم،
میبینم که معادلات زیر برقرار هستند:
5 ≡ 3P1 + 5P2 (26 به پیمانه)
2 ≡ 6P1 + 1P2
(26 به پیمانه)
که مطابق
با آنچه گفته شد، میتوانیم این دو معادله را بصورت زیر درآوریم:
1 × 5 ≡ (1×3)P1 + (1×5)P2 (26 به پیمانه)
5 × 2 ≡ (5×6)P1
+ (5×1)P2 (26 به پیمانه)
و پس از
تفریق آنها از یکدیگر، خواهیم داشت:
1 × 5 - 5 × 2 ≡ (1 × 3 - 5 × 6)P1 (26 به پیمانه)
بطور
مشابه باب میتواند معادله بالایی را در k3، و معادله پایینی را
در k1،
ضرب کند، که در اینصورت خواهیم داشت:
5
× 6 ≡ (6×3)P1 + (6×5)P2 (26
به پیمانه)
5
× 2 ≡ (3×6)P1 + (3×1)P2 (26
به پیمانه)
و اینبار
او معادله پایینی را از بالایی کم میکند:
3 × 2 - 6 × 5 ≡ (3 × 1 - 6 × 5)P2 (26 به پیمانه)
توجه
داشته باشید که در هر دو حالت ما در سمت راست یک -27
داریم، که حاصل عبارت k1k4-k2k3 است. این عدد، مبین یا دترمینان (determinant)
سیستم نامیده میشود. اگر بزرگترین مقسوم علیه مشترک دترمینان و 26، یک باشد، آنگاه دترمینان یک وارون ضربی دارد، و باب
برای یافتن P1 و P2 میتواند هر دو طرف معادله را
در این وارون ضرب کند. این شباهت زیادی با حل معادلات دو مجهوله معمولی دارد، که
در آن دو معادله با دو مجهول وقتی میتوانند حل شود که دترمینان دستگاه صفر نباشد.
همانطور
که گفته شد، در مثال قبلی دترمینان -27 است که به پیمانه 26
با 25 برابر است. اگر باب
از الگوریتم اقلیدسی استفاده کند، او خواهد دید که:
![]() ≡ 25 (26
به پیمانه)
≡ 25 (26
به پیمانه)
بنابراین
او نتیجه خواهد گرفت
P1
≡ ((1 × 5) – (5 × 2)) × 25 (26 به
پیمانه)
P2
≡ ((3 × 2) – (6 × 5)) × 25 (26 به پیمانه)
که
نهایتاً به معادلات زیر ساده میشود
P1 ≡ 5 (26 به پیمانه), P2 ≡ 24 (26 به پیمانه)
بطور کلی
اگر k1k4-k2k3
وارون داشته باشد، آنگاه جوابهای معادلات
C1
≡ k1P1 + k2P2
(26 به پیمانه)
C2
≡ k3P1 + k4P2
(26 به پیمانه)
عبارت
خواهد بود از:
P1
≡ ![]() (k4C1 - k2C2)
(26 به پیمانه)
(k4C1 - k2C2)
(26 به پیمانه)
P2
≡ ![]() (-k3C1 + k1C2)
(26 به پیمانه)
(-k3C1 + k1C2)
(26 به پیمانه)
روش حل
عمومی این دستگاه معادلات، که در آنها تعداد مجهولات و معادلات با هم یکی هستند،
به افتخار ابداع کننده آن گابریل کرامر، معمولاً به روش کرامر (Cramer rule)
معروف است. کرامر یک ریاضیدان سویسی قرن هجدهم بود که مطالعات زیادی را بر روی دستگاه
معادلات چند مجهوله انجام داد. بنظر میرسد که همین روشها کمی زودتر در اسکاتلند
توسط کالین مکلارین (Colin Maclaurin)
منتشر شدند. روش کرامر برای حل دستگاه معادلاتِ بزرگ، خیلی سریع نیست، ولی مطمئناً
برای پیدا کردن قطعاتی که در سایفر هیل از آنها استفاده میشود مناسب است.
توجه کنید که اگر ما به اعداد فوق اسامی جدید زیر را بدهیم
m1 = ![]() (k4),
(k4),
m2 = ![]() (-k2),
(-k2),
m3 = ![]() (-k3),
(-k3),
m4 = ![]() (k4 ),
(k4 ),
آنگاه میتوانیم
بنویسیم
P1 ≡ m1C1 + m2C2 (26 به پیمانه)
P2
≡ m3C1 + m4C2
(26 به پیمانه)
ما میتوانیم
این دستگاه معادلات را بعنوان معکوس دستگاه اولیه درنظر بگیریم، و همچنین میتوانیم
m1،
m2،
m3،
m4
را بعنوان نوعی ”کلید معکوس“ برای کلیدهای اولیه رمزگذاری، یعنی k1، k2، k3، k4، بحساب آوریم. در مثال ما این
کلید عبارت است از 25×1, 25×−5, 25×−6, 25×3, یا 25, 5, 6, 23 به پیمانه 26.
وقتی باب اینها را بدست آورد، روند رمزگشایی درست مانند رمزگذاری خواهد بود. این
هم نمونه دیگری از ایده ”جلو رفتن برای بازگشت به عقب“ است که قبلاً در بخش 1.3 بیان کردم.
تعیین دقیق اینکه چه تعداد کلید خوب برای سایفر هیل وجود دارد (یعنی کلیدهایی که دترمینان دارای یک وارون باشد) کمی پیچیده است، ولی برای قطعاتی به اندازه 2، تعداد آنها در حدود 45,000 و برای قطعاتی به اندازه 3 در حدود 52,000,000,000 است، بنابراین استفاده از حملات فراگیر برای شکستن آنها مشکلتر میشود. همچنین توجه داشته باشید که باب نیاز دارد بداند آیا در پایان پیام حرف پوچ وجود دارد یا نه. البته وقتی او پیام را بخواند این موضوع روشن میشود.
هیل در
سال 1930 سایفر اولیه خود را توسعه داد. مهمترین نمونه از آنها، سایفری است که
حالا عموماً سایفر هیل آفین (affine Hill cipher)
نامیده میشود. علت این نامگذاری هم این است که سایفر اولیه هیل با یک مرحله اضافی
ترکیب شده، درست مثل آنچه در مورد ترکیب سایفرهای جمعی و ضربی انجام میشود تا از
آن سایفر آفین حاصل شود. اگر باز هم اندازه قطعات را 2
بگیریم، فرمولهای جدید و گسترش یافته ما چنین خواهند بود:
C1
≡ k1P1 + k2P2
+ m1 (26 به
پیمانه)
C2
≡ k3P1 + k4P2
+ m2 (26 به
پیمانه)
حال کلید
ما شامل شش عدد k1، k2، k3، k4،
m1،
و m2
است، که همگی آنها میان 1
تا 26 هستند. در اینجا نیز
یک کلید تا وقتی خوب محسوب میشود که بزرگترین مقسوم علیه مشترک دترمینان آن (یعنی
k1k4-k2k3)
و 26 برابر 1
باشد (اعداد m1 و m2 میتوانند هر
عدد دلخواهی باشند). باب برای رمزگشایی نیاز دارد m1 را از C1
و m2 را از C2 کم کند و مانند قبل دستگاه
معادلات را حل کند.
برای یک سایفر چندنگاری، استفاده از تحلیل تکرار حروف دیگر جواب نمیدهد، زیرا همانطور که در مثال قبلی دیدید، یک حرف در متن غیررمزی همیشه معادل یکسانی در متنرمزی ندارد. بنابراین اساس این ایده که حدس بزنیم چه حرفی مثلاً معادل حرف e است، در اینجا کاربردی ندارد. از سوی دیگر ما همچنین دیدیم که قطعاتی که از حروف غیررمزی یکسانی تشکیل شدهاند، به قطعات رمزی یکسانی تبدیل میشوند، و برای قطعاتی که اندازه آنها 2 یا 3 باشد، میتوان از اینمورد بهرهبرداری کرد. برای مثال، معمولترین دونگاری (digraph)، یا بلوک 2-حرفی، که وجود دارد ”th“ است، که بر طبق یک تحقیق حدوداً در %2.5 موارد ظاهر میشود. معمولترین سهنگاری، یا بلوک 3-حرفی، که وجود دارد ”the“ است، که بر طبق همان تحقیق، در %1 از موارد ظاهر میشود. ایو میتواند از حقایقی مانند اینها استفاده کند، تا بر این اساس، یک تحلیل دونگاری یا سهنگاری را روی متنرمزی انجام دهد تا شاید بتواند رمز یک سایفر جایگزینی دونگاری یا سهنگاری را بشکند. ولی هر چه تعداد حروف قطعات بالاتر برود، انجام چنین کاری هم سریعاً دشوار میشود، زیرا قطعات زیادی میتوانند وجود داشته باشند که آنچنان تفاوت بزرگی هم در تکرار آنها وجود ندارد. هیل در سال 1929 میخواست ماشینی بسازد که در آن از مجموعهای از چرخدندهها استفاده میشد، و متون را بصورت مکانیکی با استفاده از قطعات 6تایی رمزگذاری کند. اساساً شکستن چنین سایفری با استفاده از روش تحلیل تکرار غیر ممکن بود. ولی متاسفانه هیل نتوانست ماشین خود را تکمیل کند.
سایفر هیل
هرگز کاربرد زیادی پیدا نکردند، زیرا زیاد از حد پیچیده بود، و رمزنگاری با دستگاههای
مکانیکی هم بسوی سایفرهای جایگزینی چندالفبایی رفت. با ظهور کامپیوترهای دیجیتال،
و کاربرد آنها در رمزنگاری، ایده هیل در مورد استفاده از دستگاه معادلات چند
مجهوله در رمزنگاری، اهمیت زیادی پیدا کرد. ولی با توجه به دیدگاههای جدید، این
سایفرها دارای آسیبپذیری بدی هستند که با آنچه ما قبلاً به آنها اشاره کردیم
تفاوت دارند.
تا اینجا
کلیه حملاتِ تحلیلرمز که ما آنها را توضیح دادیم، جزء حملات متمرکز بر روی متنرمزی (ciphertext-only attacks)
بودند، که در آنها آنچه ایو میداند فقط یک پیام رمزی است که بین آلیس و باب رد و
بدل شده و او آن را استراق سمع کرده. ولی فرض کنید ایو به نحوی توانسته هم به
قسمتهایی از متن غیررمزی و هم متنرمزی پیامی که آلیس فرستاده دسترسی پیدا کند. سپس او میتواند یک حمله متن غیررمزی-شناختهشده (Known plaintext attack)
را انجام دهد. در این حمله، هم متن غیررمزی، و هم متنرمزی برای ایو شناختهشده
هستند، یعنی او هر دو آنها (یا حداقل قسمتی از آنها) را میداند، و هدف
اصلی تنها یافتن کلید رمز است تا با استفاده از آن متنهای رمزی دیگری که با این کلید
رمزگذاری شدهاند شکسته شوند.
اگر از
سایفر اولیه هیل استفاده شود، که اندازه قطعات آن 2
باشد، فرض کنید ایو توانسته چهار حرف متن غیررمزی، یعنی P1، P2،
P3،
و P4،
را پیدا کند، و آنها را با حروف متنرمزی، یعنی C1، C2،
C3،
و C4،
تطابق دهد. دراینصورت او موارد زیر را میداند:
C1
≡ k1P1 + k2P2
(26 به پیمانه)
C2
≡ k3P1 + k4P2
(26 به پیمانه)
C3
≡ k1P3 + k2P4
(26 به پیمانه)
C4
≡ k3P3 + k4P4
(26 به پیمانه)
از نقطه
نظر ایو، تنها چیزی که مجهول است کلیدها هستند، بنابراین او چهار معادله با چهار مجهول
دارد که برای یافتن این کلیدها باید آنها را حل کند.
در مثال قبلی اگر ایو بتواند دو بلوک آخر متن غیررمزی را بدست آورد، آنگاه میداند که:
21 ≡ k15 + k222
(26 به پیمانه)
0
≡ k35 + k422 (26 به پیمانه)
5
≡ k15 + k224 (26 به پیمانه)
2
≡ k35 + k424 (26 به پیمانه)
در واقع
معادلات بالا دو دستگاه معادله را تشکیل میدهند:
21 ≡ k15 + k222 (26 به پیمانه)
5 ≡ k15 + k224
(26 به پیمانه)
و دیگری
0 ≡ k35 + k422 (26 به پیمانه)
2 ≡ k35 + k424
(26 به پیمانه)
که ایو میتواند
هر یک از آنها را به روش کرامر حل کند، یعنی درست به همان روشی که باب در بخش قبلی
آنها را حل کرد. برای دستگاه معادلات اول، فرمول کرامر موارد زیر را به ما میدهد:
k1
≡ ![]() (26 به پیمانه)
(26 به پیمانه)
k2
≡ ![]() (26 به
پیمانه)
(26 به
پیمانه)
اگر
محاسبات فوق را انجام دهید خواهید داشت:
k1 ≡ 3 (26 به پیمانه) و k2 ≡ 5 (26 به پیمانه)
بطور مشابه،
با حل دستگاه معادلات دوم ایو خواهد دید که:
k3
≡ ![]() (26 به پیمانه)
(26 به پیمانه)
k4
≡ ![]() (26 به
پیمانه)
(26 به
پیمانه)
که ایو با
حل آنها دو کلید آخر را نیز خواهد داشت:
k3 ≡ 6 (26 به پیمانه) و k4 ≡ 1 (26 به پیمانه)
بصورت کلی،
ایو تنها نیاز دارد به اندازه تعداد حروفی که در بلوکها قرار دارند، قطعات
غیررمزی را بدست آورد. بنابراین شکستن سایفر هیل با استفاده از حمله متنغیررمزی-شناختهشده،
به راحتی رمزگشایی یک پیام است. چنین چیزی غیرقابل قبول است، بنابراین هیچگاه
از شکل اولیه سایفر هیل استفاده نشد. ولی ایده استفاده از دستگاه معادلات در
رمزگذاری چندنگاری باعث بوجود آمدن سایفرهای زیادی در رمزنگاری نوین شده است.
من در
مقدمه این کتاب به شما یادآوری کردم که برخی از سایفرهایی که من در این کتاب به
شما معرفی میکنم، در جهان امروز منسوخ شدهاند، و این شامل کلیه سایفرهای میشود
که در این فصل و دو فصل بعدی آنها را بررسی میکنیم. از یک نظر، همه آنها بر روی
حروف الفبا کار میکنند، ولی در دنیای امروز ما میخواهیم همه چیز را رمزگذاری
کنیم، از اعداد گرفته تا تصاویر، اصوات، و بقیه اطلاعات. البته چنین چیزی یک مشکل
جدی را بوجود نمیآورد، زیرا ما بخوبی میدانیم که چگونه میتوانیم کلیه این
اطلاعات را بشکل اعداد درآوریم، و میتوانیم کلیه این سایفرها را طوری تنظیم کنیم
که بجای حروف با اعداد کار کنند. سایفرهای جمعی و ضربی به تعداد کافی کلید ندارند،
و به همین دلیل درمقابل حملات فراگیر آسیب پذیر هستند، و امروزه با در دست
بودن کامپیوترها، سایفرهای آفین نیز از کلیدهای کافی برخوردار نیستند. شاید نکته
مهمتری که وجود دارد این باشد که کلیه سایفرهای جایگزینی تکنگاری تکالفبایی
در برابر حملات تحلیل تکرار آسیب پذیر هستند. البته در رمزنگاری نوین،
سایفرهای جایگزینی تکالفبایی از اهمیت برخوردارند، زیرا آنها اساس خیلی از
سایفرهای نوین را تشکیل میدهند، از جمله سایفرهای
جایگزینی چندالفبایی، که ما آنها را در فصل 2 مورد بررسی قرار خواهیم داد. برای درک بهتر
فصل 2، شما ابتدا باید این فصل را یادگرفته باشید. سایفرهای جایگزینی
چندالفبایی امروز دیگر سایفرهای امنی محسوب نمیشوند، و دلیل آن را در پایان
فصل 2 خواهیم فهمید.
اگر
اندازه قطعات سایفرهای جایگزینی چندنگاری به اندازه کافی طولانی باشد، آنها
نسبت به حملاتِ تحلیلِ تکرار مقاوم هستند. در حقیقت نوعی از سایفرهای جدید، که سایفر بلوکی نامیده میشود، و ما آن را در فصل 5 مورد
بررسی قرار میدهیم، بعنوان یکی از سایفرهای جایگزینی چندنگاری در نظر گرفته میشود
که بر روی الفبایی عمل میکند که تنها شامل دو حرف 0
و 1 است. مثالهایی که تا اینجا
مشاهده کردهایم، یعنی سایفر هیل و سایفر آفین، در مقابل حملات متنغیررمزی-شناختهشده آسیبپذیر
هستند. بنابراین چنین سایفرهای امروزه امن حساب نمیشوند. همانطور که قبلاً اشاره
کردم، این دو سایفر اجزاء سازنده سایفرهای بلوکی جدید را تشکیل میدهند، از جمله
سایفر بلوکی فعلی دولت آمریکا، که من آن را در فصل 4 توضیح میدهم. بنابراین شما بدون اینکه
سایفر هیل را درک نکرده باشید، احتمالاً نخواهید توانست سایفرهای جدید بلوکی را
درک کنید. برای درک سایفر هیل نیز شما باید ابتدا سایفرها جمعی، ضربی، و آفین را
یادگرفته باشید.
همچنین
باید به این نکته اشاره کنم که هرچند تکنیکهای تحیل رمز که در این فصل مورد بررسی
قرار گرفتند خیلی پیشرفته نیستند، ولی هنوز هم برای درک تکنیکهای تحلیلِ رمزِ
جدید اهمیت بسیار زیادی دارند. برای سایفرهای بلوکی مدرن، تکرار حروف خیلی مطرح
نیست، ولی مطمئناً حملات تکرار حروف اهمیت دارند. برای مثال، حملات
تفاضلی که در فصل 4 آنها را بررسی میکنیم، مانند حملات تکرار حروف،
بطور سنگینی به محاسبات آماری تکرارِ حروف وابسته هستند، با این تفاوت که آنها
بجای اینکه روی متنهای رمزی بکار گرفته شوند، بر روی تفاوت آنها بکارگرفتی میشوند.
بطور مشابه حملات خطی که در فصل 4 آنها را توضیح میدهم، نسخههای پیچیده حملات
متنغیررمزی-شناختهشده هستند که قبلاً درمورد سایفر هیل آنها را توضیح دادم.
سایفرهای نوین به ندرت شامل معادلاتی هستند که سایفر هیل و سایفر آفین داشتند، ولی
برخی اوقات میتوان آنها را با چنین معادلاتی تخمین زد، و این باعث میشود که
تحلیلهای رمزی خطی از آن بهره ببرند.
نهایتاً
ممکن است شما متعجب شوید که آیا استفاده از مفاهیم و نمادگذاریهای مربوط به حساب
پیمانهای واقعاً برای توضیح مطالب این فصل لازم بودند، یا فقط توضیح سایفرها را
سادهتر میکردند. در واقع خیلی پیش از اینکه کسی بفکر استفاده از حساب پیمانهای
برای توضیح سایفرهای جمعی، ضربی، و آفین بیافتد، آنها بخوبی مورد تحلیل قرار گرفته
بودند. از سوی دیگر، سایفرهای هیل، و همینطور سایفرهای هیل آفین، از همان ابتدا
برپایه حساب پیمانهای طراحی شده بودند. چیزی که اهمیت بیشتری دارد این است که استفاده
از حساب پیمانهای برای درک سایفرهای
نمایی و سایفرهای کلید-عمومی که در فصلهای 6،
7، و 8
مورد بررسی قرار میگیرند، حیاتی هستند.
سایفرهای چندنگاری (Polygraphic) سایفرهایی هستند که
هر بار بر روی بیش از یک حرف عمل میکنند. آنها یکی از روشهایی هستند که میتوانند
سایفرها را در مقابل تحلیل تکرار حروف مقاومتر کنند. همانطور که قبلاً ذکر شد،
تحلیل چنین سایفرهایی حتی اگر اندازه بلوک آنها 3-حرفی
باشد، میتواند بصورت دستی دشوار یا حتی غیر ممکن شود، و حتی انجام ماشینی آنها هم
دشوار است. از سوی دیگر، یک سایفر چندالفبایی هنوز میتواند مانند یک سایفر تکالفبایی
در هر بار برروی یک حرف عمل کند، ولی قاعده جایگزینی از یک حرف به حرف دیگر تغییر
میکند. اینکار میتواند به سادگی این باشد که به آلیس (یعنی کسی که کار رمزگذاری
را انجام میدهد) گزینههای بیشتری بدهیم تا او از میان آنها بطور دلخواه برای
برخی از حروفِ غیررمزی (یا همه آنها)، حروف رمزی بیشتری را انتخاب کند. در
زبانشناسی دستههای دو حرفی، یا گروههای بزرگتری از حروف که املای آنها متفاوت،
ولی تلفظ آنها یکسان باشد همآوا نامیده میشوند، به همین دلیل، چنین
سایفرهایی نیز یک سایفر همآوا (homophonic cipher)
نامیده میشود. در رمزنگاری، همآواها دستههای 2
حروفی یا گروههای بزرگتری از حروف هستند که در متنرمزی بطور متفاوتی نوشته میشوند
ولی بصورت یکسانی رمزگشایی میشوند.
مانند بسیاری دیگر از جنبههای رمزنگاری، بنظر میرسد
ایده نهفته در پشت سایفرهای همآوا نیز ابتدا توسط اعراب کشف شده باشد. ولی اولین سایفر
شناخته شدهای که از همآواها بعنوان تکنیک اصلی خود استفاده کرد، در سال 1401 در
ایتالیا پیدا شد. بنظر میرسد که این سایفر نسخهای از سایفر آتباش (atbash)
باشد، که در آن از 12 علامت اضافی
استفاده شده که برای حروف a، e، o، و u، که پرتکرارترین حروف
قرن پانزدهم ایتالیا بودند از 3
علامت استفاده شده بود. اگر بخواهیم این ایده را بصورت امروزی و با استفاده از
حروف زبان انگلیسی و علائم چاپی نشان دهیم، بصورت زیر خواهد بود:

ممکن است
اینطور تصور شود که این سایفر نسبت به یک سایفر ساده بهبود زیادی حاصل نکرده، ولی
ایده نهفته در پشت آن قابل توجه است: اگر حروف رمزی که با حروف غیررمزیِ پرتکرار
متناظر شدهاند بطور تصادفی میان چندین گزینه تقسیم شوند، برای چنین سایفری تحلیلِ
تکرارِ ساده بسیار دشوار میشود. اگر این سایفر بطور درستی بکارگرفته شود، یک متنرمزی
را تولید خواهد کرد که در آن تکرار هیچ حرف پرتکراری (مثل e) حتی نزدیک %13 هم نخواهد بود. درعوض چهار علامت مختلف (V, @, &, و -)
را در متنرمزی خواهیم داشت که تکرار هر کدام از آنها بیشتر از %4 خواهد بود، بنابراین محتوای چنین سایفری کمک زیادی به
تحلیل کننده رمز نخواهد کرد. البته اینکار وقتی بخوبی جواب میدهد که آلیس یکی از
چهار علامت را بطور تصادفی انتخاب کرده باشد. دامی که ممکن است یک رمزگذار تنبل در
آن گیر کند این است که تنها از یکی از این چهار گزینه استفاده کند (مثلاً V که نسبت به بقیه
براحتی از روی صفحه کلید وارد میشود) و از حروف دیگر کمتر استفاده کند. اینکار
باعث میشود تا فایده عمده سایفرهای همآوا از بین برود.
معلوم
نیست که آیا در زمان پیدایش این سایفر در اروپای قرن پانزدهم، تحلیل تکرار حروف چقدر
شناخته شده بوده است. این حقیقت که سایفرهای اولیه، همآواها را فقط منحصر به حروف
صدادار (a,
e,o) میدادند، که تکرار آنها نسبت به بقیه حروف بیشتر است، ممکن است
این ظن را تقویت کند که آنها از این موضوع آگاه بودند. ولی از این مطمئن نیستیم،
زیرا بر خلاف جهان عرب که در آنجا رمزنگاری موضوعی بود که بیشتر جنبه دانشگاهی
داشت، در اروپای دوران رونسانس فقط برای امور سیاسیِ بسیار جدی از آن استفاده میشد،
و مطالب مربوط به آن نیز سرّی شمرده میشد. تنها در حدود سالهای 1466 یا 1467 بود
که در یکی از کتابهای نوشته لئون باتیستا آلبرتی (Leon
Battista Alberti) به مطالبی در مورد تحلیل
تکرار حروف اشاره شده بود. و شاید بدلیل محافظهکاری کلیشهای که سیاستمداران
داشتند، تنها در اواسط سالهای 1500 بود که سایفرهایی پدیدار شدند که در آنها حروف
بیصدا (consonants) نیز همآوا داشتند.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
کلیه سایفرهایی
که تا اینجا مورد بررسی قرار گرفتند از نوع سایفرهای جایگزینی بودند؛ یک حرف، یا
گروهی از حروف جایگزین حرف دیگری میشوند. حالا به ایده متفاوت دیگری میپردازیم،
یعنی بجای تغییر حروف، ما ”فقط“ آنها را به اطراف جابجا میکنیم.
مانند
سایفرهای جایگزینی، ایده سایفرهای ترانهشی (یا جابجایی) نیز به دوران باستان بازمیگردد.
نخستین نمونه ثبت شده آن ممکن است اسکایتِلی (scytale)
باشد. گفته میشود که این دستگاه رمزگذاری برای اولین بار توسط اسپارتیان باستان،
و خصوصاً توسط ژنرال لیساندر، مورد استفاده قرار گرفته بود.
از نظر
لغوی اسکایتلی به معنای عصا یا چوبدستی است، و شرح اینکه چگونه چنین چیزی ممکن است
بعنوان یک دستگاه رمزگذاری بکارگرفته شود، قرنها پس از لیساندر، اولین بار توسط
تاریخنگار رومی پلوتارک (Plutarch)
شرح داده شد.
هنگامی که شهر افورس (ephors)،
که در آن زمان پایتخت اسپارت بود، میخواست یکی از فرماندهان خودش را به جایی
بفرستد، اولین کاری که قبل از رفتن آنها میکردند این بود که بادقت دو قطعه چوب را
به طول و ضخامت یکسان میبرید، و یکی از آنها را پیش خودشان نگاه میداشتند و
دیگری را به فرمانده میدادند. این قطعات چوبی ”اسکایتلی“ نام داشتند. هنگامی که
آنها میخواستند یک پیام مهم و سّری را برای یکدیگر بفرستند، یک طومار کاغذی دراز
و باریک را که مانند یک تسمه چرمی بود میبریدند، و بدون اینکه هیچ فضای خالی در
آن باشد، آن را بدور ”اسکایتلی“ خودشان میپیچیدند، بطوری که طومار تمام طول
اسکایتلی را بپوشاند. بعد از اینکه اینکار را انجام دادند، آنها پیام مورد نظر
خودشان را خط به خط روی طومار پیچیده شده مینوشتند، و پس از آن طومار را از دور
اسکایتلی باز میکردند، و بدون اینکه اسکایتلی را همراه آن بفرستند، طومار را برای
گیرنده میفرستادند. گیرنده پیام نمیتوانست این طومار را بخواند، زیرا حروف نوشته
شده بروی آن هیچ ارتباطی با هم نداشتند و بدون ترتیب بودند، مگر اینکه گیرنده پیام
دوباره طومار را به دور اسکایتلی خودش (که باید با اسکایتلی فرستنده یکسان باشد)
بپیچد، تا حروفی که بصورت مارپیچ روی طومار نوشته شدهاند، دوباره روی اسکایتلی
ترتیب اولیه خود را بدست آورند، و گیرنده بتواند آنها را بخواند.
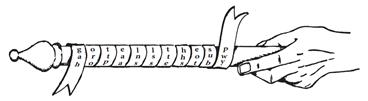
شکل 3.1- یک اسکایتلی (scytale).
بهترین
نحوی که میتوان این را توصیف کرد، مانند چیزی است که در شکل 3.1 نشان داده شده
است.
البته آلیس و باب کم و بیش میتوانند همین کار را
بدون اینکه از یک چوبدستی استفاده کنند انجام دهند. فرض کنید چوب آنقدر ضخیم هست
که بتوان 3 حرف را بر دور آن
نوشت، و همچنین آنقدر دراز هست که طومار بتواند 11
دور به دور آن بپیچد. در اینصورت آلیس یک جدول 3×11
را دارد که میتواند حروف غیررمزی خود را در آن بنویسد. اگر پیام تمامی جدول را پر
نکند، آلیس میتواند برای پر کردن فضای باقیمانده از حروف پوچ (nulls)
استفاده کند.
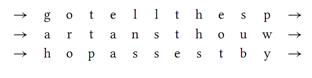
توجه داشته باشید که اگر آلیس پیام خود را بر روی یک
اسکایتلی واقعی بنویسد، هر ستون دور متفاوتی از کاغذ خواهد بود. آنگاه پیام رمزی
بجای خواندن سطری، از خواندن ستونی (یا بعبارتی، باز کردن کاغذ پیچانده شده) حاصل
میشود.

یا
GAHOR OTTPE AALNS LSSTT EHHSE OTSUB
PWYAZ
وقتی
رمزگذاری اسکایتلی با استفاده از چنین مستطیلی انجام شود، معمولاً به آن ترانهش ستونی (columnar transposition)
میگویند. مانند آنچه ما در بخش 2.2 انجام دادیم، معمولاً رسم است که متنرمزی را
به دستههای پنج حرفی تقسیم میکنند. به منظور اینکه طول واقعی پیام دقیقاً معلوم
نباشد، جاهای خالی آخرین دسته را با پوچها پر میکنند. همانطور که بزودی خواهید
دید، نباید برای ایو معلوم باشد که چه حروفی پوچ هستند.
آیا این سایفر دارای کلید هم هست؟ مطابق با گفته
پلوتارک، ”ما به دو قطعه چوب گرد نیاز داریم که که ضخامت و طول آنها دقیقاً یکسان
باشد،“ یکی برای باب و دیگری برای آلیس. تا آنجا که به کار ما مربوط است، آنقدر که
لازم است ضخامت چوبها با هم برابر باشند، طول آنها مهم نیست. اگر ایو سعی کند
پیام رمزی را با چوبی رمزگشایی کند که ضخامت آن بجای سه حرف، مثلاً چهار حرف باشد،
آنگاه وقتی او کاغذ را بدور چوب میپیچاند چنین چیزی را خواهد گرفت:

بعبارت
دیگر، متنرمزی بصورت ستونی نوشته شده و بصورت سطری خوانده میشود. اگر ایو پیام
فوق را بصورت سطری بخواند، شما میتوانید ببینید که هیچ معنی ندارد.
از سوی دیگر، اگر باب متنرمزی را با استفاده از یک
چوب درست، یا یک جدول درست، رمزگشایی کند، اگر متنرمزی را بصورت ستونی بنویسد،
آنگاه پیام زیر را خواهد گرفت:
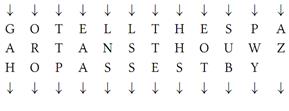
بدلیل
اینکه آخرین ستون تنها یک ستون جزئی است، باب میداند که این باید یک حرف پوچ
باشد. او آن را دور میاندازد و بدون هیچ مشکلی متن غیررمزی را بصورت سطری میخواند.
بنابراین،
کلید سایفر اسکایتلی محیط چوب، یا بطور معادل، تعداد سطرهای جدول است، که در مثال
ما 3 میباشد. توجه داشته
باشید که اگر آلیس خانههای اضافی را با حروف پوچ پر نکند، آنگاه حدس اینکه کلید
چیست برای ایو ساده خواهد بود.
او میداند که یک جدول مستطیلی با 33 حرف غیررمزی پر شدهاند، بنابراین چهار حالت برای این جدول وجود دارد: 1×33،3×11 ،11×3 ، و 33×1.
اولین و آخرین موارد بیمایه هستند، بنابراین یافتن کلید برای ایو آسان خواهد بود.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
برخی
اوقات میان سایفرهای جایگزینی چندنگاری و سایفرهای جایگزینی چندلفظی (polyliteral) فرق گذاشته میشود.
همانطور که در بخش 1.6 دیدیم، در سایفرهای چندنگاری، بلوکی متشکل
از حروف غیررمزی به بلوکی از حروف غیررمزی با همان اندازه تبدیل میشود. از سوی
دیگر، سایفرهای چندلفظی یک حرفِ تکی را به بلوکی از حروف یا علامتها تبدیل میکنند.
بعنوان اولین مثال، ما دوباره به یونان باستان بازمیگردیم. در قرن دوم پیش از
میلاد، مورخ یونانی پولیبیوس (Polybius)،
یک کتاب 40 جلدی درمورد تاریخ یونان و روم نوشت که در آن به موضوعات فرعی، از جمله
رمزنگاری، و علامت دادن با آتش نیز پرداخته بود. ممکن است پلیبیوس اولین نویسندهای
باشد که بین کدها و سایفرها تمایز قائل میشود و چندین مثال از فرستادن پیامهای
رمزی با استفاده از مشعل مطرح میکند. ولی این سایفر است که در اینجا برای ما جالب
است. پولیبیوس مینویسد:
”ما الفبا را
برداشته و آن را به پنج قسمت تقسیم میکنیم، که هر یک پنج حرف دارند. قسمت آخر یک
حرف کم دارد[2]،
ولی این تاثیری در کار ما ندارد. هر یک از دوطرفی که میخواهند پیامی را برای
یکدیگر بفرستند باید پنج لوح در دست داشته باشند و یکی از قسمتهای الفبا را روی
آن بنویسند. حالا پیکی که پیام را میبرد اولین دسته از مشعلهایی که در سمت چپ
قرار دارند را بالا میبرد تا مشخص کند کدام لوح مورد نظر است، به این صورت که اگر
لوح اول موردنظر است، یک مشعل، اگر لوح دوم موردنظر است، دو مشعل، و به همین
ترتیب. سپس او درست به همین شکل، شروع به بالا بردن دسته دوم مشعلها میکند که در
سمت راست قرار دارند تا مشخص کند گیرنده پیام باید کدامیک از حروف را بنویسد.“
در شکل جدید این روش، معمولاً بجای 5 لوح از یک جدول 5 ×
5 استفاده میشود، و این سیستم عموماً مربع پلیبیوس (Polybius square)
نامیده میشود. بدلیل اینکه الفبای مدرن انگلیسی بجای 25حرف، 26
حرف دارد، یا باید از یکی از آنها صرفنظر کنیم، یا دوتای آنها را در یک خانه قرار
دهیم (معمولاً i و j را در یک خانه قرار میهند). آنگاه
این مربع یا جدول بشکل زیر خواهد بود:

پس اگر آلیس بخواهد متن ”I fear the Greeks“
را رمزگذاری کند، بصورت زیر خواهد بود:

اگر متن
رمزی را بصورت پنجتایی مرتب کنیم، خواهیم داشت:
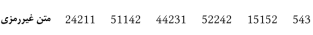
بدلیل
اینکه هریک از حروف متن غیررمزی به یک متن دو رقمی تبدیل شدهاند، این سایفر دولفظی (biliteral) نامیده میشود.
مانند خیلی از سایفرهای دنیای باستان، این سایفر نیز کلید ندارد، گرچه میتوان با
مشخص کردن ترتیب حروف در مربع، یعنی تعداد حروف از بالا به پایین، یا از چپ به
راست، یا هر دو، برای این سایفر نیز کلیدی را مشخص کرد.
نسخهای از این سایفر که برای حروف الفبای انگلیسی
مناسبتر است، بصورت زیر میباشد:

یکی از همین مربعها که برای الفبای 29 حرفی زبانهای
دانمارکی و نروژی مناسب است را در زیر میبینید:

ممکن است شما فکر کنید که مورد فوق بدردنخور است،
ولی من میخواهم توجه شما را به تبدیلی جلب کنم که از آن حاصل میشود:
![]()
صرف نظر
از صفرها، تنها کاری که ما انجام دادهایم تبدیل حروف به اعداد است! زیرا اگر ما
خانه سمت چپ بالا را خالی بگذاریم، حرفی که در سطر rام و ستون cام قرار دارد، (r.10+c)امین حرف الفبا است.
ولی در سیستم عادی عددنویسی، این عدد بصورت rc نمایش داده میشود،
یعنی رقم r در چپ که بدنبال آن در راست رقم c نوشته شده. برای مثال، حرفی که در سطر 2
و ستون 3 قرار دارد w است، که میشود (2.10+3)=23امین حرف الفبای انگلیسی، دانمارکی، یا
نروژی.
خوب تکلیف نسخه انگلیسی جدول به چه شکل خواهد بود؟
تبدیلی که صورت میگیرد بصورت زیر خواهد بود:
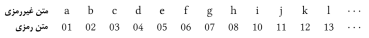
حالا حرفی
که در سطر r و ستون c
قرار دارد (9.r+c)امین
حرف الفبا خواهد بود. برای مثال، حرفی که در سطر 2 و ستون 7
قرار دارد، y
است، که (2.9+7)=25امین حرف
الفبا است. ولی اگر بجای اینکه این عدد را در مبنای 10 بنویسیم، آن را در مبنای 9
بنویسیم، آنگاه بصورت 27
در میآید.
اگر ما از پایههای کوچکی مثل 3
برای عدد نویسی استفاده کنیم، آنگاه برای نوشتن اعدادی که نشاندهنده حروف باشند، 2 رقم کافی نیست. یک راه که میتوان این مشکل را حل کرد
این است که از چندین جدول استفاده کنیم و شماره آن جدول را قبل از ارقام سطر یا
ستون بگذاریم:
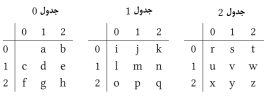
که به ما این را میدهد:
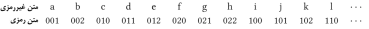
حالا ما یک سیستم سهلفظی داریم. حرفی که در جدول
شماره t،
سطر r،
و ستون c
قرار دارد، (t.32+r.3+c)امین
حرف الفبا است. برای مثال حرفی که در جدول 2،
در سطر 0، ستون 1 قرار دارد s است که میشود
(2.9+0.3+1)=19امین حرف
الفبا. اگر استفاده از چند جدول پردردسر بنظر میرسد، از یک جدول نیز میتوان استفاده
کرد، و ارقامی که در سطرها، ستونها، یا هر دو قرار دارند را گروهبندی کرد:

عددنویسی
در مبنای 2، که به آن باینری (binary)
هم میگویند، کاربرد گستردهای در کامپیوتر دارد، و به همین دلیل استفاده از آنها
در سایفرهای نوین بسیار متداول است. اگر از این اعداد استفاده کنیم، ما به جداول
تو در توی زیادی نیاز داریم، بنابراین آنها را بصورت زیر گروهبندی میکنیم:
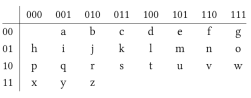
که در
اینصورت خواهیم داشت:
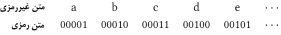
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
اساساً سایفرهایی
که تا اینجای کتاب مورد بررسی قرار گرفتند، چه آنهایی که قدیمی بودند و چه آنهایی
که جدید، همه از نوع سایفرهای
بلوکی (block
ciphers) هستند. کاری که آنها میکنند این است که متن غیررمزی
را به بلوکهای (قطعات) نسبتاً بزرگی تقسیم میکنند. این بلوکها
ممکن است شامل یک یا چند حرف، یا یک یا چند بیت باشند. چیزی که برای هر بلوک اتفاق
میافتاد مستقل از چیزی است که برای بلوکهای قبلی یا بعدی آن اتفاق میافتاد. روش
دیگر، استفاده از یک سایفر
دنبالهای (stream
cipher) است، که در آن حروف، بیتها، یا بلوکهای کوچک در یک
زمان رمزگذاری میشوند، و نتیجه هر رمزگذاری ممکن است به آنچه در رمزگذاریهای
قبلی اتفاق افتاده بستگی داشته باشد. این روش میتواند چندین مزیت داشته باشد. یکی
از این مزیتها این است که شما از قبل نمیدانید طول پیام غیررمزی چقدر است و نمیخواهید
خودتان را درگیر انتقال لایهگذاری (padding)
کنید. ارتباطات بیسیم (wireless)
نمونه خوبی از اینمورد است. مزیت دیگر این است که در این نوع سایفرها پخش بصورت
خودکار انجام میگیرد، و بدلیل اینکه عملیاتی که در آشفتگی سهیم هستند میتوانند
در طول رمزگذاری بر روی هم انباشته شوند، این امکان وجود دارد که بتوان با استفاده
از یک عملیات ساده و سریع، آشفتگی خوبی را حاصل کرد.
اولین قدم در راه سایفرهای دنبالهای، استفاده از
سایفرهای چندالفبایی کلیددار است که در بخش 2.4 آنها
را بررسی کردیم. معلوم است که هرچقدر طول کلمهکلیدی یا کلیدعبور کوتاهتر باشد،
شکستن سایفر نیز سادهتر خواهد بود. بنظر میرسد رمزنگاران اولیه بر این باور
بودند که طول کلمهکلیدی نباید از یک جمله تجاوز کند، و گرنه، بیشتر از اینکه
فایده داشته باشد، دردسرساز میشود. همانطور که در فصل 2 دیدیم،
درحالی که فنون تحلیلرمز پیشرفت میکرد، معلوم شد که میتوان از کلیدهای تکراری
برای شکستن رمز بهرهبرداری کرد. تا پایان قرن نوزدهم رسم بر این بود که بجای کلمهکلیدی
از یک متنکلیدی (keytext)
استفاده شود که طول آن میتوانست به اندازه متن غیررمزی باشد. این متنکلیدی مثلاً
میتوانست متنی باشد که از آغاز یک صفحه خاص از یک کتاب خاص باشد، که قبلاً بر روی
آن توافق شده بود. با استفاده از یک سایفر جدول مربعی که در بخش 2.4
توضیح دادیم، ما میتوانیم متن خودمان را بصورت زیر رمزگذاری کنیم:

حتی تحلیلرمز
سایفرهای چندالفبایی کلید-تکراری برای تحلیلگران رمز مشکل بود و موجب میشد آنها
بدنبال راههای سادهتری باشند. سایفرهای
کلید-جاری (running-key
ciphers)، که کلید تکرار نمیشود، حتی از آنها هم مشکلترند،
گرچه شکستن آنها غیر ممکن نیست.
در اینجا دو حالت اصلی وجود دارد. یک حالت این است که
ایو چندین پیام را در دست داشته باشد که با کلید جاری یکسانی رمزگذاری شده باشند.
و حالت سختتر این است که او تنها یک پیام تکی را در دست داشته باشد. اگر ایو ظنین
باشد که چند پیامی که او در دست دارد با کلید یکسانی رمزگذاری شدهاند، او میتواند
با استفاده از آزمود کاپا که در بخش 2.5 توضیح دادیم این را بررسی کند. اگر نتیجه
آزمون منفی بود، او میتواند این امکان را نیز در نظر بگیرد که ممکن است متنها با
کلید یکسانی رمزگذاری شدهاند ولی رمزگذاری از مکانهای مختلف کلید شروع شده است.
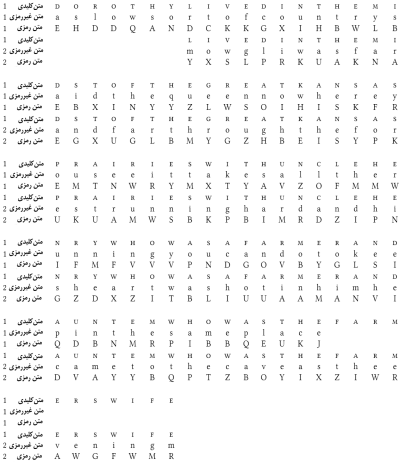
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
ما میخواهیم
سایفری داشته باشیم که هم از نظر ریاضی ساده باشد و هم در برابر حملات متمرکز بر
روی متنرمزی و هم در برابر حملات متنغیررمزی-شناختهشده مقاوم باشد. برای مورد
اول ما یک سایفر چندنگاری را انتخاب میکنیم، هرچند روشی که در اینجا بلوکها را
میسازیم با آنچه در بخش 1.6 کردیم کمی تفاوت دارد. در اینجا نیز ما 2 را بعنوان اندازه بلوک انتخاب میکنیم و متن غیررمزی
خودمان را به بلوکهای دو حرفی تقسیم میکنیم. برای مثال، فرض کنید متن غیررمزی ما
”power to
the people“ باشد:
po we rt ot he pe op le
در اینجا
ما هر بلوک 2-حرفی را با بهم چسباندن اعداد مربوط به حروف آنها، به یک عدد تبدیل
میکنیم، و در جایی که لازم باشد 0
میگذاریم:

ما همچنین
نیاز داریم برای این سایفر یک پیمانه را انتخاب کنیم. در اینجا پیمانه 26 دیگر جواب نمیدهد، زیرا اعداد مربوط به بلوکها میتوانند
به بزرگی 2626 باشند. بهتر است برای
پیمانه از عددی استفاده کنیم که اول باشد، هر چند بعداً در این فصل خواهیم دید که
چگونه میتوانیم این مشکل را دور بزنیم. فعلاً بنظر میرسد عدد 2819 برای اینکار مناسب باشد، چون هم اول است و هم از 2626 بزرگتر.
ما قبلاً
از جمع، ضرب، و ترکیبات مختلف آنها استفاده کردیم. ایده ریاضی بعدی این است که از نما (exponentiation)، یا بعبارتی به توان رساندن اعداد استفاده کنیم. حتماً بخاطر دارید که بتوان
رساندن یک عدد به این معنی است که عدد مورد نظر مکرراً در خودش ضرب شود. برای
مثال، 23=2×2×2=8.
به ویژه ما از فرمول زیر استفاده خواهیم کرد:
C≡Pe (2819 به
پیمانه)
بطور سنتی کلید این سایفر e نامیده میشود، زیرا e مخفف encryption exponent
است، که به معنای نمای رمزگذاری میباشد. توجه داشته باشید که در اینجا e
با عدد 2.71828... که پایه لگاریتم
طبیعی است ارتباطی ندارد. با رعایت برخی محدودیتها که بعداً توضیح میدهم، نمای
رمزگذاری عددی بین 1 تا 2818 است. فعلاً بیایید e را برابر 769 بگیریم.

کاری که
دراینجا انجام میدهیم این است که 1615
را بتوان 769 میرسانیم، و هربار
به 2819 رسیدیم دوباره
به اول باز میگردیم. این یعنی اینکه محاسبات زیادی باید انجام شود. برای اینکار شما
به یک کامپیوتر، یا حداقل یک ماشین حساب خیلی خوب، نیاز دارید. ما نمیتوانیم همه
این بلوکها را دوباره به حروف تبدیل کنیم، ولی این مهم نیست. آلیس میتواند فقط
اعداد را برای باب بفرستد.
باب چگونه
این اعداد را رمزگشایی میکند؟ همانطور که معکوس جمع تفریق، و معکوس ضرب تقسیم
است، معکوس بتوان رساندن نیز ریشه گرفتن است. برای مثال اگر 8=23،
آنگاه ![]() ، و اگر C=Pe،
آنگاه
، و اگر C=Pe،
آنگاه ![]() . ولی اگر فکر میکنید
تقسیم کردن و گرفتن یک عدد صحیح مشکل بود، گرفتن ریشه و گرفتن یک عدد صحیح به
مراتب از آن مشکلتر است. برای مثال اولین بلوک متن رمزی ما 1592
بود و 769امین ریشه عدد 1592
تقریباً برابر 1.0096 است، که برای ما
کاملاً بیفایده است.
. ولی اگر فکر میکنید
تقسیم کردن و گرفتن یک عدد صحیح مشکل بود، گرفتن ریشه و گرفتن یک عدد صحیح به
مراتب از آن مشکلتر است. برای مثال اولین بلوک متن رمزی ما 1592
بود و 769امین ریشه عدد 1592
تقریباً برابر 1.0096 است، که برای ما
کاملاً بیفایده است.
به منظور
اینکه در رمزگشایی پیام به باب کمک کنیم، باید نسبت به آنچه تا کنون بیان کردیم،
کمی عمیقتر به نظریه اعداد وارد شویم. تا اینجای کار ما تنها از یک ایده بزرگ
ریاضی، بنام حساب پیمانهای استفاده کردیم، که بوسیله گاوس فرمول بندی شده بود.
حالا ما به ایده بزرگ دیگری نیاز داریم که عمدتاً به پییر فرما (Pierre de Fermat)
نسبت داده میشود. فرما در فرانسه و در قرن هفدهم بدنیا امد. شغل اصلی او قاضی
بود، و بعنوان ریاضیدان آماتور نیز کار میکرد. او وقتی میخواست اعلام کند که چیزی
را اثبات کرده، همیشه عادت داشت در اینمورد به همکاران خودش نامه بنویسد. و در این
نامهها بجای اینکه اثباتی را ارائه دهد، او گیرنده نامه را به چالش میکشید و از
او میخواست قضیه را ثابت کند. او همچنین ادعا کرد که چیزی را اثبات کرده که بعداً
معلوم شد اشتباه است. او همچنین ادعا کرد که چیزی را اثبات کرده که امروزه بنام آخرین قضیه فرما شناخته میشود. هر چند سیصد سال طول کشید که صحت
این ادعا تایید شود، ولی حالا معلوم شده که اثبات آن بسیار سختتر از آن چیزی بود
که فرما فکر میکرده.
آن واقعیت
ریاضی، یا به عبارتی، آن قضیه که ما در اینجا برای کارمان به آن نیاز داریم، و
فرما ادعا کرده بود صحت آن را اثبات کرده، قطعاً صحیح است و ممکن است خود فرما برای
آن اثباتی در دست داشته، اما مانند همیشه او این اثبات را در جایی ننوشته بود.
هرچند این قضیه پیامدهای بزرگی را به دنبال داشت، ولی به قضیه کوچک فرما (Fermat’s little theorem)
معروف است. ما دقیقاً نمیدانیم که فرما چگونه آن را کشف کرد، ولی با استفاده از
ایدههایی که قبلاً آنها را نشان دادیم، مثالهایی را مطرح میکنیم که میتواند در
کشف این قضیه به شما کمک کنند.
فرض کنید با یک سایفر ضربی کار میکنید که الفبای
بسیار کوچکی دارد و تعداد این الفبا یک حرف اول است. برای مثال، الفبای 13-حرفی هاوایایی
(Hawaiian)
برای این مورد جواب میدهد. اگر کلید ما 3
باشد، جدول این الفبا بصورت زیر خواهد بود:
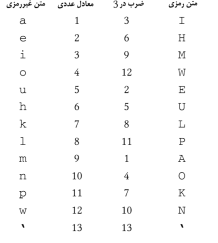
...........................................
برای ادامه مطالعه این فصل نسخه
کامل PDF کتاب را تهیه کنید.
در طول
این کتاب، ما چند چیز را در مورد آلیس، باب، و ایو فرض گرفتهایم. اولین فرض این
است که آلیس و باب باید پیش از فرستادن پیام با هم ملاقات کنند تا بر سر کلیدی که
از آن استفاده میکنند با هم توافق کنند. آنها نیاز دارند این ملاقات را در جایی
انجام دهند که ایو نتواند مکالمات آنها را بشنود، یا اینکه روشی برای ارتباط پیدا
کنند که ایو نتواند آن را شنود کند. چنین چیزی آنقدر معقول و ضروری بود که برای
بیش از 2000 سال هیچ کس بطور جدی آن را زیر سئوال نبرد. ممکن است برای آلیس و باب
امن نباشد تا با یکدیگر ملاقات کنند، ولی آنها بر روی اینکه این ملاقات کی انجام
شود کنترل دارند و حقیقتاً لازم هم نیست این ملاقات طولانی باشد، بنابراین در
بیشتر مواقع چنین ملاقاتی امکان پذیر است. اغلب در تاریخ دیده شده که آلیس و باب
هیچ چیزِ از قبل مشخص شدهای را ندارند که با یکدیگر رد و بدل کنند؛ به هر صورت،
در مواقع اضطراری آلیس یک پیام سرّی را میفرستد و امیدوار است باب آنقدر باهوش
باشد که آن را بفهمد، و ایو نتواند از آن سر درآورد. چنین چیزی ریسک بزرگی محسوب
میشود و نمیتوان آن را بعنوان اساس یک سیستم امن بحساب آورد.
در سال
1974 رالف مرکل (Ralph Merkle)
که تازه آخرین ترم دوران کارشناسی خود را در دانشگاه کالفرنیا طی میکرد، درسی
درباره امنیت کامپیوتری برداشت. در آن درس کمی هم مباحث مربوط به رمزنگاری مطرح
شده بود، ولی هنوز استاندارد DES بطور رسمی اعلام نشده بود، و
چیز زیادی در مورد رمزنگاری موجود نبود. ولی چیزی در آنجا بود که توجه مرکل را به
خودش جلب کرد و موجب شد به این فکر بیافتد که آیا راهی هست که بتوان از فرضی که
همه آن را پذیرفتهاند اجتناب کرد یا نه. و این یعنی آیا امکان دارد بدون اینکه
آلیس و باب از
قبل بر روی کلیدی با هم توافق کرده باشند، آلیس بتواند پیامی را برای باب بفرستد؟
روشن است که باید کلیدی در کار باشد، ولی آیا ممکن است آلیس و باب بتوانند توسط
فرایندی بر روی این کلید توافق کنند که ایو نتواند آن را بفهمد، حتی اگر به
ارتباطات آنها گوش دهد یا آن را ببیند؟ مرکل ایده اولیه اینکار را منتشر کرد، ایدهای
که بعدها آن را ”ساده، ولی کارآمد“ توصیف کرد. در واقع توضیح این ایده تنها در یک
و نیم صفحه جای میگرفت، ولی مرکل سعی کرد تا در چهار و نیم صفحه این ایده را
توجیه کند، مشکلات آن را شرح دهد، و اهمیت آن را توضیح دهد. او نمیتوانست برای
این مطالب منبعی را ذکر کند، زیرا ظاهراً کسی قبلاً حتی فکر چنین ایدهای هم به
ذهنش خطور نمیکرد. تعجب برانگیز نیست که استاد راهنمای وی این ایده را درست
نفهمیده بود و به او پیشنهاد میدهد بر روی پروژه دیگری کار کند. ولی در عوض مرکل
این کلاس را رها میکند و به کار بر روی این پروژه ادامه میدهد.
ایده مرکل، که امروزه به معماهای مرکل (Merkle’s puzzles)
نیز معروفند، چند بار مورد تجدید نظر قرار گرفته، و آنچه در اینجا توضیح میدهیم
نسخهای است که نهایتاً منتشر شد. آلیس کار خود را با ایجاد تعداد زیادی از پیامهای
رمزگذاری شده (یعنی همان معماها) شروع میکند، و آنها را برای باب میفرستد (به
شکل 7.1 نگاه کنید). تابع رمزگذاری باید چنان باشد که شکستن هر معما به روش
جستجوی فراگیر ”بسیار سخت، ولی ممکن“ باشد. مرکل پیشنهاد میکند که از سایفری استفاده
شود که کلید آن 128-بیتی باشد، و مشخص میکند
که تنها از بخش کوچکی از کلیه کلیدهای ممکن استفاده میشود. در اینجا ما از یک
مثال بسیار کوچک و یک سایفر جمعی استفاده میکنیم:
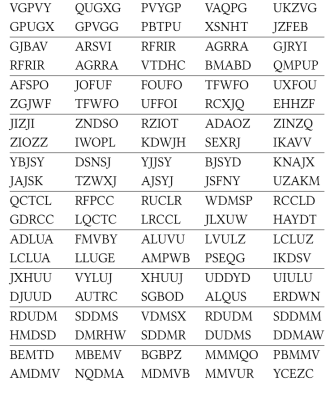

شکل 7.1- شروع معماهای مرکل.
آلیس برای
باب شرح میدهد که هر معما شامل سه مجموعه اعداد است که او بطور تصادفی انتخاب
کرده، و همه آنها با کلید یکسانی رمزگذاری شدهاند. اولین عدد، عدد شناسه (ID) است که مشخص کننده
معما است. دومین عدد یک کلید سرّی از یک سایفر امن است، که درواقع آلیس و باب میتوانند
از آن برای ارتباط استفاده کنند. در اینجا نیز مرکل یک سایفر 128-بیتی را پیشنهاد میدهد، ولی اجازه میدهد از کلیه
کلیدهای ممکن استفاده شود. در اینجا نیز برای سادگی کار، ما از یک سایفر هیل 2×2 استفاده میکنیم. آخرین عدد برای همه معماها یکسان است
و نوعی وارسی (check) است که توسط آن باب
بتواند مطمئن شود که آیا او معما را درست حل کرده یا نه. در مثال ما عدد وارسی 17 است. نهایتاً برای اینکه طول کلیه معماها یکسان باشد،
آنها با حروف پوچ تصادفی لایی گذاری میشوند.
باب بطور
تصادفی یکی از معماها را انتخاب کرده و با استفاده از جستجوی فراگیر آن را حل میکند،
سپس از عدد وارسی استفاده میکند که ببیند آیا او معما را درست حل کرده یا نه. پس
از آن، همانطور که در شکل 7.2 نشان داده شده، او عدد شناسه (ID)، که در معما
رمزگذاری شده بود را برای آلیس میفرستد. برای مثال اگر او یکی از معماها را بصورت
زیر باشد حل کرده باشد:
twent ynine teent
wenty fives
evenf ourse vente
enait puvfh
آنگاه میداند
که شناسه عددی 20 (twenty)
و کلید مخفی19,25,7,4 (nineteen, twentyfive,
seven, four) است. او 20
را برای آلیس میفرستد.

شکل 7.2-باب معما را حل میکند.
آلیس
فهرستی از متنهای غیر رمزی دارد که به ترتیب شناسه عددی (ID) مرتب شدهاند:

...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
حالا ما
میدانیم که آلیس میتواند بدون اینکه از قبل با باب ملاقات کرده باشد، از دو طریق
پیامی را بطور امن برای او بفرستد. آنها میتوانند از سیستم توافق-کلید برای انتخاب
کلید یک سایفر کلید-متقارن استفاده کنند، یا اینکه میتوانند از یک سیستم نامتقارن
استفاده کنند که آلیس کلید عمومی رمزگذاری باب را میداند ولی فقط باب است که کلید
خصوصی رمزگشایی را در دست دارد. راه سومی نیز وجود دارد که از رمزگذاری
کلید-متقارن استفاده میکند و به آلیس اجازه میدهد بدون اینکه، چه بطور خصوصی، و
چه عمومی از قبل با باب بر روی کلیدی توافق کرده باشند، برای او پیام بفرستد. نام این سیستم پروتکل سه-گذری (three-pass protocol)
است. این سیستم برای کاربردهای عمومی خیلی کارآمد نیست، ولی جالب است، و بعضی
اوقات میتواند مفید باشد.
اگر ما بتوانیم رمزنگاری کلید-نامتقارن را مانند یک
درِ قفل شده فرض کنیم که در آن شکافی برای گذاشتن نامهها قرار دارد، آنگاه میتوانیم
رمزنگاری کلید-متقارن را مانند چمدانی فرض کنیم که دارای قفلی است که دو کلید
یکسان دارد. اگر آلیس بخواهد پیامی را برای باب بفرستد، او این پیام را در چمدان
قرار میدهد و درِ آن را با کلید خودش قفل میکند. هنگامی که باب چمدان را دریافت
میکند، او با کلید دیگری که خودش دارد در را باز کرده و پیام را میخواند (به شکل 8.1 نگاه کنید).
شکل 8.1- رمزگذاری کلید-متقارن.
حالا فرض کنید که جاقفلی چمدان طوری است که هم میتوان
در آن یک قفل قرار داد و هم دو قفل، و آلیس و باب قفلهایی دارند که کلید آنها با
هم فرق میکند. آلیس پیام را در چمدان میگذارد، قفل خودش را نیز در جاقفلی میگذارد
و چمدان را برای باب میفرستد (شکل 8.2). این اولین گذر از پروتکل سه-گذری است.
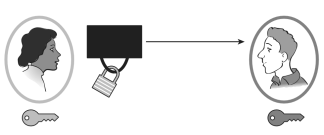
شکل 8.2- گذر اول پروتکل سه- گذری.
بدلیل اینکه باب کلید آلیس را دراختیار ندارد نمیتواند
قفل او را باز کند. ولی در عوض او قفل خودش را در جاقفلی میگذارد و آن را برای
آلیس پس میفرستد
(شکل 8.3). این دومین گذر از پروتکل سه-گذری است.
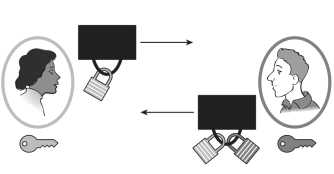
شکل 8.3- گذر دوم پروتکل سه- گذری.
حالا
همانطور که در شکل 8.4 نشان داده شده آلیس قفل خودش را بازمیکند و چمدان را به باب پس میفرستد،
این گذر سوم است. توجه داشته باشید که هنوز قفل باب بر روی چمدان هست، بنابراین
ایو نمیتواند آن را باز کند. حالا باب میتواند قفل خود را از روی جاقفلی بردارد
و پیام را بخواند. در طول این سه رفت و برگشت (سه گذر)، هیچگاه چمدان بدون قفل
نبوده، و آلیس و باب هم هرگز نیازی به اشتراک، یا تبادل، کلید نداشتهاند.
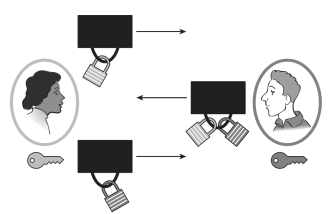
شکل 8.4- گذر سوم پروتکل سه- گذری.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
همانطور
که چندین بار در طول این کتاب اشاره کردم، درحال حاضر امنیت سایفرهای کلید عمومی بر
اساس دشواری ظاهری برخی از مسائل معروفِ ریاضی، مثل لگاریتم گسسته و تجزیه اعداد،
قرار دارند. هیچ کس نتوانسته راه سادهای برای حل این مسائل پیدا کند، ولی کسی هم
نتوانسته ثابت کند که چنین راههایی وجود ندارند. بنابراین همیشه احتمال این هست
که فردا کسی پیدا شود و اعلام کند که به تکنیکهای ریاضی جدیدی دست یافته که میتواند
این رمزها را بشکند.
حتی اگر
تکنیکهای ریاضی جدیدی نیز پیدا نشود، همیشه این امکان وجود دارد که نوع جدیدی از
کامپیوترها بتوانند این سایفرها را ناامن کنند. محتملترین کامپیوترهایی که برای
این قبیل کارها مناسبند، آنهایی هستند که بر پایه فیزیک کوانتوم کار میکنند.
هرچند تا به امروز هنوز کسی یک کامپیوتر کوانتومی را به نمایش نگذاشته که بتواند
مسائل جِدی را حل کند، ولی با اینحال در چند دهه اخیر محققان راههایی را برای
برنامهریزی چنین کامپیوترهایی پیدا کردهاند. این حوزه جدید، محاسبات کوانتومی (quantum computing)
نام دارد و ممکن است برای رمزنگاری عواقب مهمی را دربر داشته باشد.
احتمالاً معروفترین چیزی که باعث میشود فیزیک
کوانتوم از فیزیک کلاسیک متمایز بنظر بیایید برهمنهش (superposition)
است، یعنی ایده اینکه یک ذره کوانتومی (مثل گربه فرضی شرودینگر) در آنِ واحد میتواند
بیشتر از یک حالت داشته باشد. در سال 1935 فیزیکدانی بنام اروین شرودینگر (Erwin Schrödinger)
این سئوال را مطرح کرد که اگر گربهای را در یک جعبه کاملاً دربسته، که نه میتوان
درون آن را دید و نه میتوان صدایی از آن شنید، قرار دهیم، چه اتفاقی خواهد افتاد.
مقدار کمی ماده رادیواکتیو نیز در درون جعبه قرار داده شده، بطوری که در طول یک
ساعت %50 احتمال دارد که
یک اتم فروبپاشد و %50
نیز احتمال داشت که هیچ اتفاقی نیافتد. اگر در درون جعبه یک شمارگر گایگر (Geiger
counter) قرار داده شده باشد و این دستگاه یک فروپاشی را پیدا
کند، این باعث میشود تا بطور اتوماتیک درِ غذای گربه باز شود، و اگر چیزی پیدا
نشود، در هم باز نمیشود. سئوال این است که در پایان یک ساعت، آیا گربه سیر است یا
گرسنه؟ (به شکل 9.1 نگاه کنید).
شکل 9.1- آیا گربه شرودینگر سیر است یا گرسنه؟
بر اساس
فیزیک کوانتوم، تا وقتی ما در جعبه را باز نکردهایم تا ببینیم وضعیت چطور است،
اتم هم حالتِ فروپاشی دارد و هم ندارد، بنابراین گربه هم گرسنه است و هم سیر. درست مانند حالتِ گربه که همزمان میتواند
در دو وضعیت مختلف قرار داشته باشد، یک بیت
کوانتومی (quantum
bit)، یا کیوبیت (qubit)،
نیز بجای اینکه یک مقدار را داشته باشد، همزمان هم میتواند 0
باشد و هم 1.
در محاسبات کوانتومی خواص زیادی هست که باعث میشود
چنین چیزی برای حل مسائل مربوط به رمزنگاری مناسب بنظر برسد. فرض کنید ما با
استفاده از یک کامپیوتر کوانتومی بخواهیم یک عدد، (مثلاً 4)
را تجزیه کنیم. ما کار خود را با دستهای از کیوبیتها شروع میکنیم و آنها را
طوری تنظیم میکنیم که نمایشدهنده عدد ما بصورت باینری باشند. شکل باینری عدد 4 بصورت 100
است. حالا ما دسته دیگری از کیوبیتها را گرفته و آنها را طوری تنظیم میکنیم که
نشاندهنده یک عامل ممکن باشند. ولی بجای اینکه همه عوامل ممکن را یک به یک امتحان
کنیم، ما کیوبیتهای عامل را بصورت زیر قرار میدهیم
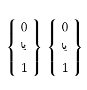
تا هر کیوبیت همزمان 0
و 1 باشد. آنها روی هم چیزی را
تشکیل میدهند که ”عدد
کوانتومی“ (qunumber)
نام دارد، که یا 0، 1، 2،
یا 3 است.
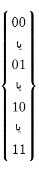
ما به دنبال عاملهای کوچکتر از 4 هستیم، پس تا اینجا درست پیش رفتیم. آنگاه میتوانیم 4 را بر اعداد کوانتومی تقسیم کنیم، و اگر خارج قسمت عددی
کوچکتر از 4 بود آن را نگاه داریم
و اگر نبود 0 را چاپ کنیم. ما
کیوبیتهای زیر را میگیریم

حالا باید
بخش دیگر آزمایش فکری شرودینگر را در نظر داشته باشیم که میگوید ”تا وقتی در جعبه باز نشود، گربه هم گرسنه
و هم سیر است، ولی وقتی ما در را باز کردیم و به داخل جعبه نگاه کردیم، گربه
ناگهان به یکی از این حالتها "فرومیریزد" (collapse)“.
اگر این را بر تجزیه کوانتومی خودمان اعمال کنیم، نتیجه خواهیم گرفت که اگر ما
خروجی کامپیوتر کوانتومی را بررسی کنیم، برخی اوقات 00 را میگیریم، که نه یک مقسومعلیه غیربدیهی است و نه مفید. و برخی اوقات
هم 10 را میگیریم، که
بدلیل اینکه 2 مقسومعلیه 4 میباشد، مفید است. ولی ما میتوانیم این کار را با یک
الگوریتم احتمالی هم انجام دهیم، پس صرفِ استفاده از برهمنهش فایدهای برای ما
نداشته است.
ولی ما میتوانیم از یکی دیگر از جنبههای فیزیک
کوانتوم نیز استفاده کنیم. مدلی که در شکل 9.2 نشان داده شده را در نظر بگیرید. یک
ذره زیراتمی، مثل الکترون یا فوتون، به طرف یک جداکننده
پرتو (beam
splitter) فرستاده میشود. برای مثال، اگر ذره مورد نظر یک فوتون
باشد، جداکننده پرتو میتواند یک آینه نیم-نقرهپوش باشد. اگر ما مکرراً این کار
را انجام دهیم، نیمی از مواقع ذره از جداکننده پرتو عبور میکند و نیمی از مواقع
به جهات دیگر پرتاب میشود، که دقیقاً همان چیزی است که ما در آشکارکنندهها
مشاهده میکنیم (شکل 9.3). تا اینجا رفتار ذره تماماً با اصول احتمالی تطابق دارد.
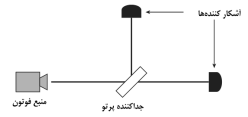
شکل 9.2- آزمایشی با یک جداکننده پرتو.
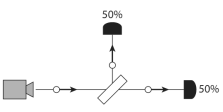
شکل 9.3- هر یک از آشکارکنندهها نیمی از مواقع یک ذره را
ثبت میکنند.
حالا مدلی
که در شکل 9.4 نشان داده شده را درنظر بگیرید. در اینجا ما دو جداکننده و دو مانع
کاملاً منعکس کننده (مثل آینههایی که کاملاً نقره پوش هستند) داریم، که همیشه
ذرات از روی آنها به اطراف پرتاپ میشوند. اگر هر جداکننده نیمی از مواقع ذرات را
عبور دهد، دو مسیر ممکن به سوی آشکارکننده وجود دارد، که احتمال یکسان است.
شکل 9.4- آزمایشی با دو جداکننده پرتو.
بنابراین ما هنوز انتظار داریم که نیمی از مواقع ذره
به هر یک از آشکارکنندهها برسد. ولی این لزوماً چیزی نیست که اتفاق میافتاد.
درعوض، بسته به جزئیات دقیق تنظیم آزمایش، ممکن است ما ببینیم که در تمام مواقع
ذره در یک آشکار کننده ظاهر میشود (به شکل 9.5 نگاه کنید).
شکل 9.5- یک از آشکار
کنندهها هرگز فوتونی را ثبت نمیکند و یکی دیگر همیشه ثبت میکند.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
[1]
- بعد از k
حرف l میآید و قاعدتاً برای کلید دوم باید از این حرف استفاده شود. ولی چون حرف
l
شباهت زیادی با عدد 1 دارد، رمزنگاران ترجیح میدهند
برای اینکار از حرف m
استفاده کنند.
[2]
- در زمان پلیبیوس تعداد حروف الفبا 24 عدد بود.